Cara mencari nilai p dari skor t di excel
Seringkali dalam statistik, uji hipotesis akan menghasilkan statistik uji T-score. Setelah kami menemukan skor-t tersebut, kami biasanya menemukan nilai p yang terkait dengannya. Jika nilai p ini berada di bawah tingkat alfa tertentu (misalnya 0,10, 0,05, 0,01), maka kami menolak hipotesis nol pengujian tersebut dan menyimpulkan bahwa hasil kami signifikan.
Tutorial ini menjelaskan cara mencari nilai p dari skor-t di Excel menggunakan fungsi T.DIST , yang menggunakan argumen berikut:
T.DIST (x, derajat_kebebasan)
Emas:
- x : Skor T yang menarik minat kami.
- deg_freedom : Derajat kebebasan.
Mari kita lihat beberapa contoh.
Contoh 1: Nilai P dari t-score (dua sisi)
Seorang ahli botani ingin mengetahui apakah tinggi rata-rata suatu spesies tumbuhan tertentu sama dengan 15 inci. Dalam sampel acak 12 tanaman, ia menemukan bahwa rata-rata tinggi sampel adalah 14,33 inci dan simpangan baku sampel adalah 1,37 inci.
Lakukan uji hipotesis dua sisi menggunakan tingkat alfa 0,05 untuk menentukan apakah tinggi rata-rata sama dengan 15 inci.
Langkah 1: Nyatakan hipotesisnya.
Hipotesis nol (H 0 ): μ = 15
Hipotesis alternatif: (Ha): μ ≠ 15
Langkah 2: Temukan T-score dan derajat kebebasan.
skor t = ( x -μ) / (s/√n) = (14.33-15) / (1.37/√12) = -1.694 .
derajat kebebasan = n-1 = 12-1 = 11 .
Langkah 3: Temukan nilai p dari t-score menggunakan Excel.
Untuk mencari nilai p dari t-score, kita akan menggunakan rumus berikut di Excel:
=T.DIST.2T(ABS(-1.694), 11)
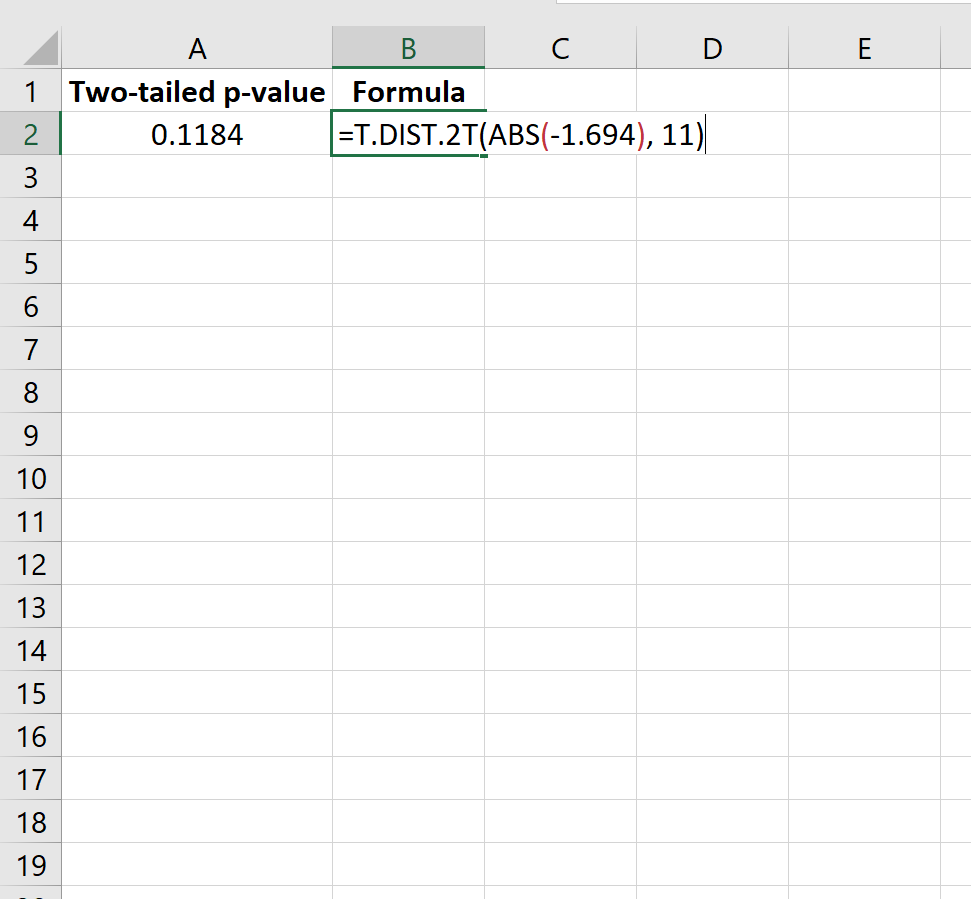
Ini memberitahu kita bahwa nilai p dua sisi adalah 0,1184 .
Langkah 4: Tolak atau jangan tolak hipotesis nol.
Karena nilai p sebesar 0,1184 tidak kurang dari tingkat alfa yang dipilih sebesar 0,05 , kami gagal menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa rata-rata tinggi tanaman berbeda dari 15 inci.
Contoh 2: Nilai P dari skor T (satu sisi)
Sebuah perusahaan ingin mengetahui apakah baterai jenis baru memiliki umur rata-rata lebih lama dibandingkan baterai standar saat ini, yang memiliki umur rata-rata 18 jam. Dalam sampel acak 25 baterai baru, mereka menemukan bahwa masa pakai rata-rata adalah 19 jam dengan deviasi standar 4 jam.
Lakukan uji hipotesis satu sisi menggunakan tingkat alpha 0,05 untuk menentukan apakah rata-rata umur baterai baru lebih lama dari rata-rata umur baterai standar saat ini.
Langkah 1: Nyatakan hipotesisnya.
Hipotesis nol (H 0 ): μ ≤ 18
Hipotesis alternatif: (Ha): μ > 18
Langkah 2: Temukan T-score dan derajat kebebasan.
skor t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1,25 .
derajat kebebasan = n-1 = 25-1 = 24 .
Langkah 3: Temukan nilai p dari t-score menggunakan Excel.
Untuk mencari nilai p dari t-score, kita akan menggunakan rumus berikut di Excel:
=T.DIST.RT(1.25, 24)
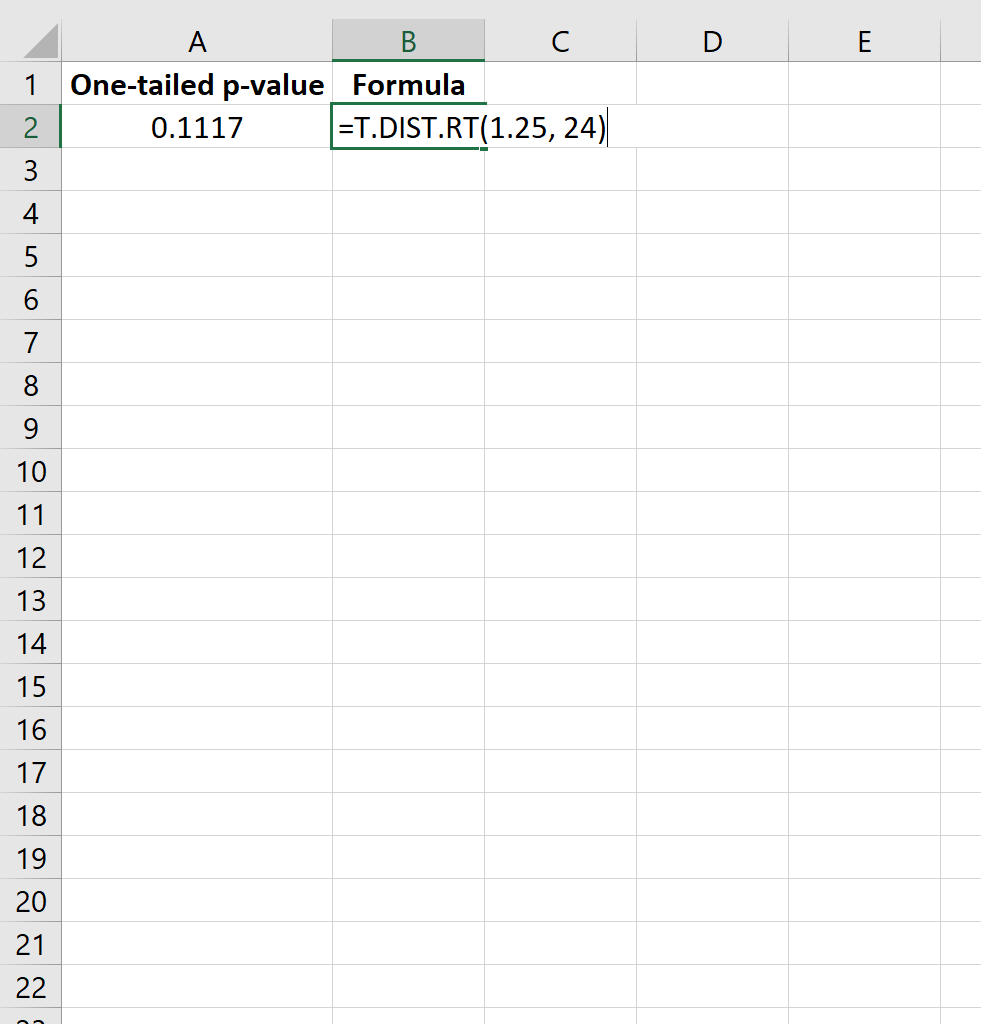
Ini memberitahu kita bahwa nilai p satu sisi adalah 0,1117 .
Langkah 4: Tolak atau jangan tolak hipotesis nol.
Karena nilai p sebesar 0,1117 lebih besar dari tingkat alfa yang dipilih sebesar 0,05 , kami gagal menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa rata-rata umur baterai baru lebih lama dari rata-rata umur baterai standar saat ini.
Untuk tutorial lebih lanjut tentang statistik di Excel, pastikan untuk membaca daftar lengkap panduan Excel kami .