Cara melakukan analisis bivariat dengan python: dengan contoh

Istilah analisis bivariat mengacu pada analisis dua variabel. Anda dapat mengingat ini karena awalan “bi” berarti “dua”.

Tujuan analisis bivariat adalah untuk memahami hubungan antara dua variabel

Ada tiga cara umum untuk melakukan analisis bivariat:

1. Titik awan

2. Koefisien korelasi

3. Regresi linier sederhana

Contoh berikut menunjukkan cara melakukan masing-masing jenis analisis bivariat ini dengan Python menggunakan pandas DataFrame berikut yang berisi informasi tentang dua variabel: (1) Jam yang dihabiskan untuk belajar dan (2) Nilai ujian yang diperoleh 20 siswa berbeda:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. Titik awan

Kita dapat menggunakan sintaks berikut untuk membuat diagram sebar antara jam belajar versus hasil ujian:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

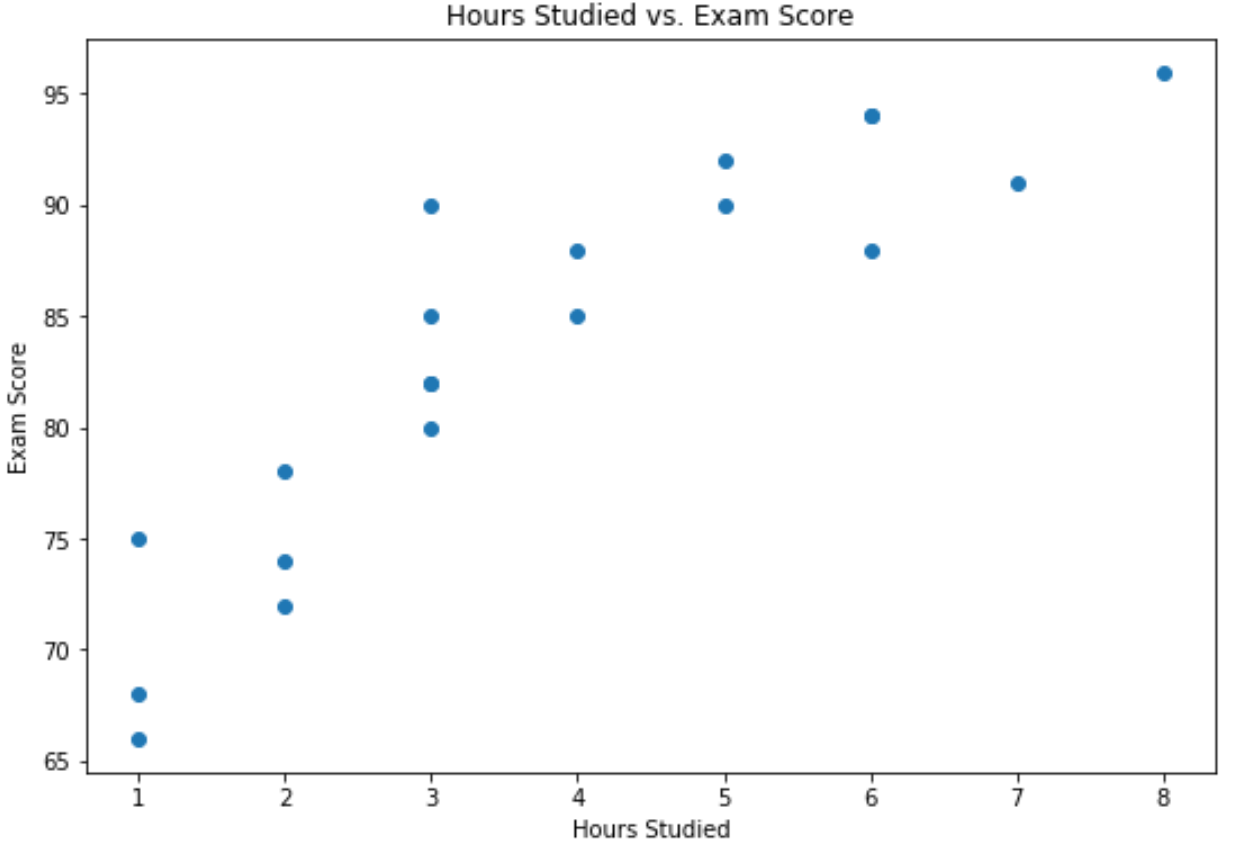
Sumbu x menunjukkan jam belajar dan sumbu y menunjukkan nilai yang diperoleh pada ujian.

Grafik tersebut menunjukkan adanya hubungan positif antara kedua variabel: seiring bertambahnya jumlah jam belajar, nilai ujian juga cenderung meningkat.

2. Koefisien korelasi

Koefisien korelasi Pearson adalah cara untuk mengukur hubungan linier antara dua variabel.

Kita dapat menggunakan fungsi corr() di pandas untuk membuat matriks korelasi:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

Koefisien korelasinya ternyata 0,891 . Hal ini menunjukkan korelasi positif yang kuat antara jam belajar dan nilai ujian.

3. Regresi linier sederhana

Regresi linier sederhana adalah metode statistik yang dapat kita gunakan untuk mengukur hubungan antara dua variabel.

Kita dapat menggunakan fungsi OLS() dari paket statsmodels untuk dengan cepat menyesuaikan model regresi linier sederhana selama berjam-jam belajar dan hasil ujian yang diterima:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

Persamaan regresi yang dipasang ternyata menjadi:

Nilai ujian = 69,0734 + 3,8471*(jam belajar)

Hal ini menunjukkan bahwa setiap tambahan jam belajar dikaitkan dengan peningkatan rata-rata nilai ujian sebesar 3,8471 .

Kita juga dapat menggunakan persamaan regresi yang disesuaikan untuk memprediksi skor yang akan diterima siswa berdasarkan jumlah jam belajar.

Misal seorang siswa yang belajar selama 3 jam seharusnya mendapat nilai 81.6147 :

• Nilai ujian = 69,0734 + 3,8471*(jam belajar)
• Nilai ujian = 69,0734 + 3,8471*(3)
• Hasil ujian = 81.6147

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang analisis bivariat:

Pengantar Analisis Bivariat
5 contoh data bivariat di kehidupan nyata
Pengantar Regresi Linier Sederhana
Pengantar Koefisien Korelasi Pearson