Cara melakukan analisis bivariat di r (dengan contoh)

Istilah analisis bivariat mengacu pada analisis dua variabel. Anda dapat mengingat ini karena awalan “bi” berarti “dua”.

Tujuan analisis bivariat adalah untuk memahami hubungan antara dua variabel

Ada tiga cara umum untuk melakukan analisis bivariat:

1. Titik awan

2. Koefisien korelasi

3. Regresi linier sederhana

Contoh berikut menunjukkan cara melakukan masing-masing jenis analisis bivariat menggunakan kumpulan data berikut yang berisi informasi mengenai dua variabel: (1) Jumlah jam belajar dan (2) Nilai ujian yang diperoleh 20 siswa berbeda:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. Titik awan

Kita dapat menggunakan sintaks berikut untuk membuat sebar jam belajar versus nilai ujian di R:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

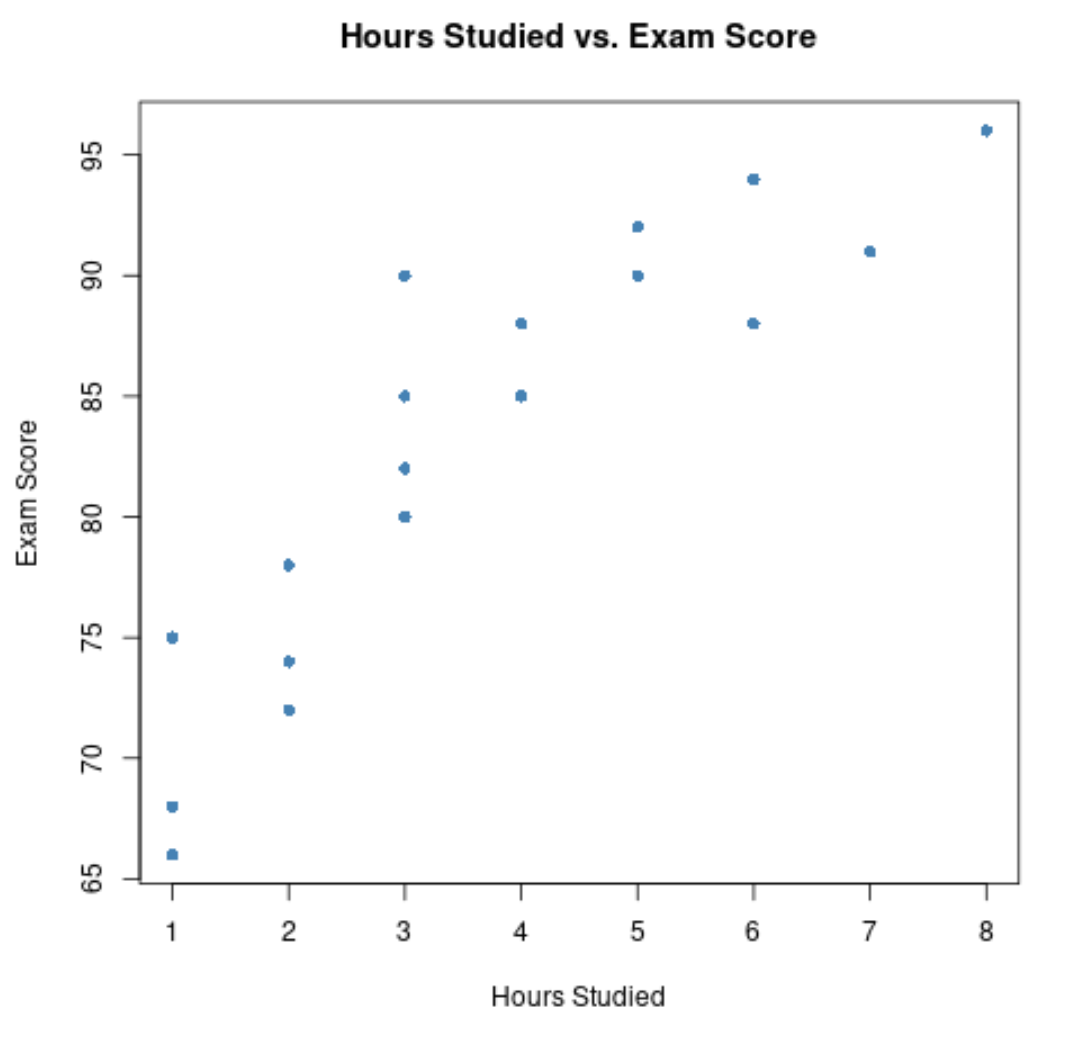
Sumbu x menunjukkan jam belajar dan sumbu y menunjukkan nilai yang diperoleh pada ujian.

Grafik tersebut menunjukkan adanya hubungan positif antara kedua variabel: seiring bertambahnya jumlah jam belajar, nilai ujian juga cenderung meningkat.

2. Koefisien korelasi

Koefisien korelasi Pearson adalah cara untuk mengukur hubungan linier antara dua variabel.

Kita dapat menggunakan fungsi cor() di R untuk menghitung koefisien korelasi Pearson antara dua variabel:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

Koefisien korelasinya ternyata 0,891 .

Nilai ini mendekati 1, menunjukkan korelasi positif yang kuat antara jam belajar dan nilai ujian.

3. Regresi linier sederhana

Regresi linier sederhana adalah metode statistik yang dapat kita gunakan untuk mencari persamaan garis yang paling “sesuai” dengan sekumpulan data, yang kemudian dapat kita gunakan untuk memahami hubungan pasti antara dua variabel.

Kita dapat menggunakan fungsi lm() di R agar sesuai dengan model regresi linier sederhana selama berjam-jam belajar dan hasil ujian yang diterima:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

Persamaan regresi yang dipasang ternyata menjadi:

Nilai ujian = 69,0734 + 3,8471*(jam belajar)

Hal ini menunjukkan bahwa setiap tambahan jam belajar dikaitkan dengan peningkatan rata-rata nilai ujian sebesar 3,8471 .

Kita juga dapat menggunakan persamaan regresi yang disesuaikan untuk memprediksi skor yang akan diterima siswa berdasarkan jumlah jam belajar.

Misal seorang siswa yang belajar selama 3 jam seharusnya mendapat nilai 81.6147 :

• Nilai ujian = 69,0734 + 3,8471*(jam belajar)
• Nilai ujian = 69,0734 + 3,8471*(3)
• Hasil ujian = 81.6147

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang analisis bivariat:

Pengantar Analisis Bivariat
5 contoh data bivariat di kehidupan nyata
Pengantar Regresi Linier Sederhana