Analisis diskriminan linier di r (langkah demi langkah)

Analisis diskriminan linier adalah metode yang dapat Anda gunakan ketika Anda memiliki sekumpulan variabel prediktor dan ingin mengklasifikasikan variabel respons ke dalam dua kelas atau lebih.

Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan analisis diskriminan linier di R.

Langkah 1: Muat Perpustakaan yang Diperlukan

Pertama, kami akan memuat perpustakaan yang diperlukan untuk contoh ini:

 library (MASS)
library (ggplot2)

Langkah 2: Muat data

Untuk contoh ini, kita akan menggunakan kumpulan data iris yang terpasang di R. Kode berikut menunjukkan cara memuat dan menampilkan kumpulan data ini:

 #attach iris dataset to make it easy to work with
attach(iris)

#view structure of dataset
str(iris)

'data.frame': 150 obs. of 5 variables:
 $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...

Kita dapat melihat bahwa dataset tersebut berisi 5 variabel dan total 150 observasi.

Untuk contoh ini, kita akan membangun model analisis diskriminan linier untuk mengklasifikasikan spesies bunga tertentu.

Kami akan menggunakan variabel prediktor berikut dalam model:

• Sepal.panjang
• Sepal.Lebar
• Kelopak. Panjang
• Kelopak. Lebar

Dan kita akan menggunakannya untuk memprediksi variabel respon Spesies , yang mendukung tiga kelas potensial berikut:

• setosa
• versikolor
• Virginia

Langkah 3: Skalakan data

Salah satu asumsi utama analisis diskriminan linier adalah bahwa setiap variabel prediktor mempunyai varian yang sama. Cara sederhana untuk memastikan asumsi ini terpenuhi adalah dengan menskalakan setiap variabel sedemikian rupa sehingga memiliki rata-rata 0 dan deviasi standar 1.

Kita dapat melakukan ini dengan cepat di R menggunakan fungsi scale() :

 #scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])

Kita dapat menggunakan fungsi apply() untuk memverifikasi bahwa setiap variabel prediktor kini memiliki rata-rata 0 dan deviasi standar 1:

 #find mean of each predictor variable
apply(iris[1:4], 2, mean)

 Sepal.Length Sepal.Width Petal.Length Petal.Width 
-4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 

#find standard deviation of each predictor variable
apply(iris[1:4], 2, sd) 

Sepal.Length Sepal.Width Petal.Length Petal.Width 
           1 1 1 1

Langkah 4: Buat sampel pelatihan dan pengujian

Selanjutnya, kita akan membagi kumpulan data menjadi kumpulan pelatihan untuk melatih model dan kumpulan pengujian untuk menguji model:

 #make this example reproducible
set.seed(1)

#Use 70% of dataset as training set and remaining 30% as testing set
sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3))
train <- iris[sample, ]
test <- iris[!sample, ] 

Langkah 5: Sesuaikan model LDA

Selanjutnya, kita akan menggunakan fungsi lda() dari paket MASS untuk mengadaptasi model LDA ke data kita:

 #fit LDA model
model <- lda(Species~., data=train)

#view model output
model

Call:
lda(Species ~ ., data = train)

Prior probabilities of groups:
    setosa versicolor virginica 
 0.3207547 0.3207547 0.3584906 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa -1.0397484 0.8131654 -1.2891006 -1.2570316
versicolor 0.1820921 -0.6038909 0.3403524 0.2208153
virginica 0.9582674 -0.1919146 1.0389776 1.1229172

Coefficients of linear discriminants:
                    LD1 LD2
Sepal.Length 0.7922820 0.5294210
Sepal.Width 0.5710586 0.7130743
Petal.Length -4.0762061 -2.7305131
Petal.Width -2.0602181 2.6326229

Proportion of traces:
   LD1 LD2 
0.9921 0.0079 

Berikut cara menginterpretasikan hasil model:

Kelompokkan probabilitas sebelumnya: Ini mewakili proporsi setiap spesies dalam set pelatihan. Misalnya, 35,8% dari seluruh observasi di set pelatihan ditujukan untuk spesies virginica .

Rata-rata kelompok: Ini menampilkan nilai rata-rata setiap variabel prediktor untuk setiap spesies.

Koefisien Diskriminan Linier: Ini menampilkan kombinasi linier variabel prediktor yang digunakan untuk melatih aturan keputusan model LDA. Misalnya:

• LD1: 0,792 * panjang sepal + 0,571 * lebar sepal – 4,076 * panjang kelopak – 2,06 * lebar kelopak
• LD2: 0,529 * panjang sepal + 0,713 * lebar sepal – 2,731 * panjang kelopak + 2,63 * lebar kelopak

Proporsi Jejak: Ini menampilkan persentase pemisahan yang dicapai oleh setiap fungsi diskriminan linier.

Langkah 6: Gunakan model untuk membuat prediksi

Setelah kita memasang model menggunakan data pelatihan, kita dapat menggunakannya untuk membuat prediksi pada data pengujian:

 #use LDA model to make predictions on test data
predicted <- predict (model, test)

names(predicted)

[1] "class" "posterior" "x"   

Ini mengembalikan daftar dengan tiga variabel:

• kelas: kelas yang diprediksi
• posterior: Probabilitas posterior bahwa suatu observasi termasuk dalam setiap kelas
• x: Diskriminan linier

Kami dapat dengan cepat memvisualisasikan masing-masing hasil ini untuk enam observasi pertama dalam kumpulan data pengujian kami:

 #view predicted class for first six observations in test set
head(predicted$class)

[1] setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica

#view posterior probabilities for first six observations in test set
head(predicted$posterior)

   setosa versicolor virginica
4 1 2.425563e-17 1.341984e-35
6 1 1.400976e-21 4.482684e-40
7 1 3.345770e-19 1.511748e-37
15 1 6.389105e-31 7.361660e-53
17 1 1.193282e-25 2.238696e-45
18 1 6.445594e-22 4.894053e-41

#view linear discriminants for first six observations in test set
head(predicted$x)

         LD1 LD2
4 7.150360 -0.7177382
6 7.961538 1.4839408
7 7.504033 0.2731178
15 10.170378 1.9859027
17 8.885168 2.1026494
18 8.113443 0.7563902

Kita dapat menggunakan kode berikut untuk melihat berapa persentase pengamatan model LDA yang memprediksi spesies dengan benar:

 #find accuracy of model
mean(predicted$class==test$Species)

[1] 1

Ternyata model tersebut memprediksi spesies dengan tepat untuk 100% observasi dalam kumpulan data pengujian kami.

Di dunia nyata, model LDA jarang memprediksi dengan tepat hasil setiap kelas, tetapi kumpulan data iris ini dibuat sedemikian rupa sehingga algoritme pembelajaran mesin cenderung bekerja dengan sangat baik.

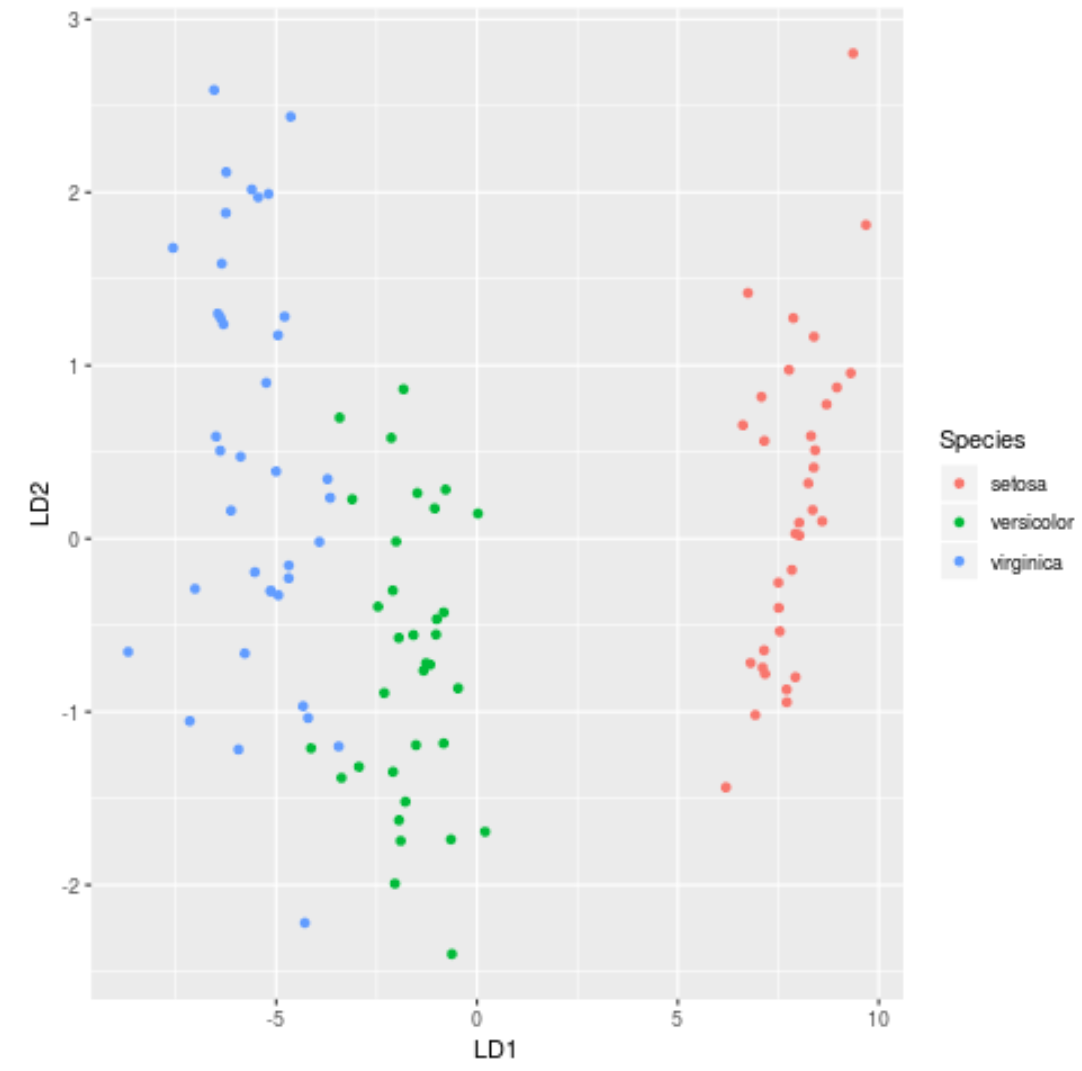
Langkah 7: Visualisasikan hasilnya

Terakhir, kita dapat membuat plot LDA untuk memvisualisasikan diskriminan linier model dan memvisualisasikan seberapa baik model tersebut memisahkan tiga spesies berbeda dalam kumpulan data kita:

 #define data to plot
lda_plot <- cbind(train, predict(model)$x)

#createplot
ggplot(lda_plot, aes (LD1, LD2)) +
  geom_point( aes (color=Species))

Anda dapat menemukan kode R lengkap yang digunakan dalam tutorial ini di sini .