Analisis komponen utama di r: contoh langkah-demi-langkah
Analisis komponen utama, sering disingkat PCA, adalah teknik pembelajaran mesin tanpa pengawasan yang berupaya menemukan komponen utama – kombinasi linier dari prediktor asli – yang menjelaskan sebagian besar variasi dalam kumpulan data.
Tujuan PCA adalah untuk menjelaskan sebagian besar variabilitas dalam suatu kumpulan data dengan variabel yang lebih sedikit dibandingkan kumpulan data aslinya.
Untuk kumpulan data tertentu dengan variabel p , kita dapat memeriksa plot sebar dari setiap kombinasi variabel berpasangan, namun jumlah plot sebar dapat menjadi besar dengan sangat cepat.
Untuk prediktor p , terdapat awan titik p(p-1)/2.
Jadi, untuk kumpulan data dengan p = 15 prediktor, akan terdapat 105 plot sebar yang berbeda!
Untungnya, PCA menawarkan cara untuk menemukan representasi kumpulan data berdimensi rendah yang menangkap sebanyak mungkin variasi data.
Jika kita dapat menangkap sebagian besar variasi hanya dalam dua dimensi, kita dapat memproyeksikan semua observasi dari kumpulan data asli ke dalam plot sebar sederhana.
Cara kita mencari komponen utamanya adalah sebagai berikut:
Diberikan kumpulan data dengan prediktor p : _
- Z m = ΣΦ jm _
- Z 1 adalah kombinasi linier dari prediktor yang menangkap varians sebanyak mungkin.
- Z 2 adalah kombinasi linier berikutnya dari prediktor yang menangkap varian terbanyak namun ortogonal (yaitu, tidak berkorelasi) dengan Z 1 .
- Z 3 kemudian merupakan kombinasi linier berikutnya dari prediktor yang menangkap varian terbanyak namun ortogonal terhadap Z 2 .
- Dan seterusnya.
Dalam praktiknya, kami menggunakan langkah-langkah berikut untuk menghitung kombinasi linier dari prediktor asli:
1. Skalakan setiap variabel agar mempunyai rata-rata 0 dan deviasi standar 1.
2. Hitung matriks kovarians untuk variabel berskala.
3. Hitung nilai eigen matriks kovarians.
Dengan menggunakan aljabar linier, kita dapat menunjukkan bahwa vektor eigen yang sesuai dengan nilai eigen terbesar adalah komponen utama pertama. Dengan kata lain, kombinasi prediktor khusus ini menjelaskan varian terbesar dalam data.
Vektor eigen yang sesuai dengan nilai eigen terbesar kedua adalah komponen utama kedua, dan seterusnya.
Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan proses ini di R.
Langkah 1: Muat data
Pertama-tama kita akan memuat paket Tidyverse , yang berisi beberapa fungsi berguna untuk memvisualisasikan dan memanipulasi data:
library (tidyverse)
Untuk contoh ini, kami akan menggunakan kumpulan data Penangkapan AS yang dibangun ke dalam R, yang berisi jumlah penangkapan per 100.000 penduduk di setiap negara bagian AS pada tahun 1973 karena pembunuhan , penyerangan , dan pemerkosaan .
Ini juga mencakup persentase penduduk setiap negara bagian yang tinggal di daerah perkotaan, UrbanPop .
Kode berikut menunjukkan cara memuat dan menampilkan baris pertama kumpulan data:
#load data data ("USArrests") #view first six rows of data head(USArrests) Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Arizona 8.1 294 80 31.0 Arkansas 8.8 190 50 19.5 California 9.0 276 91 40.6 Colorado 7.9 204 78 38.7
Langkah 2: Hitung komponen utama
Setelah memuat data, kita dapat menggunakan fungsi bawaan R prcomp() untuk menghitung komponen utama kumpulan data.
Pastikan untuk menentukan skala = TRUE sehingga setiap variabel dalam kumpulan data diskalakan agar memiliki rata-rata 0 dan deviasi standar 1 sebelum menghitung komponen utama.
Perhatikan juga bahwa vektor eigen di R mengarah ke arah negatif secara default, jadi kita akan mengalikannya dengan -1 untuk membalikkan tandanya.
#calculate main components results <- prcomp(USArrests, scale = TRUE ) #reverse the signs results$rotation <- -1*results$rotation #display main components results$rotation PC1 PC2 PC3 PC4 Murder 0.5358995 -0.4181809 0.3412327 -0.64922780 Assault 0.5831836 -0.1879856 0.2681484 0.74340748 UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773 Rape 0.5434321 0.1673186 -0.8177779 -0.08902432
Terlihat bahwa komponen utama pertama (PC1) memiliki nilai yang tinggi untuk pembunuhan, penyerangan, dan pemerkosaan, yang menunjukkan bahwa komponen utama ini menggambarkan variasi yang paling besar pada variabel-variabel tersebut.
Kita juga dapat melihat bahwa komponen utama kedua (PC2) memiliki nilai yang tinggi untuk UrbanPop, yang menunjukkan bahwa komponen utama ini menekankan pada penduduk perkotaan.
Perhatikan bahwa skor komponen utama untuk setiap negara bagian disimpan di results$x . Kami juga akan mengalikan skor ini dengan -1 untuk membalikkan tandanya:
#reverse the signs of the scores results$x <- -1*results$x #display the first six scores head(results$x) PC1 PC2 PC3 PC4 Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581 Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454 Arizona 1.7454429 0.7384595 -0.05423025 0.826264240 Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554 California 2.4986128 1.5274267 -0.59254100 0.338559240 Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164
Langkah 3: Visualisasikan hasilnya dengan biplot
Selanjutnya, kita dapat membuat biplot – plot yang memproyeksikan setiap observasi dalam kumpulan data ke dalam plot sebar yang menggunakan komponen utama pertama dan kedua sebagai sumbu:
Perhatikan bahwa skala = 0 memastikan bahwa panah dalam plot diskalakan untuk mewakili pembebanan.
biplot(results, scale = 0 )
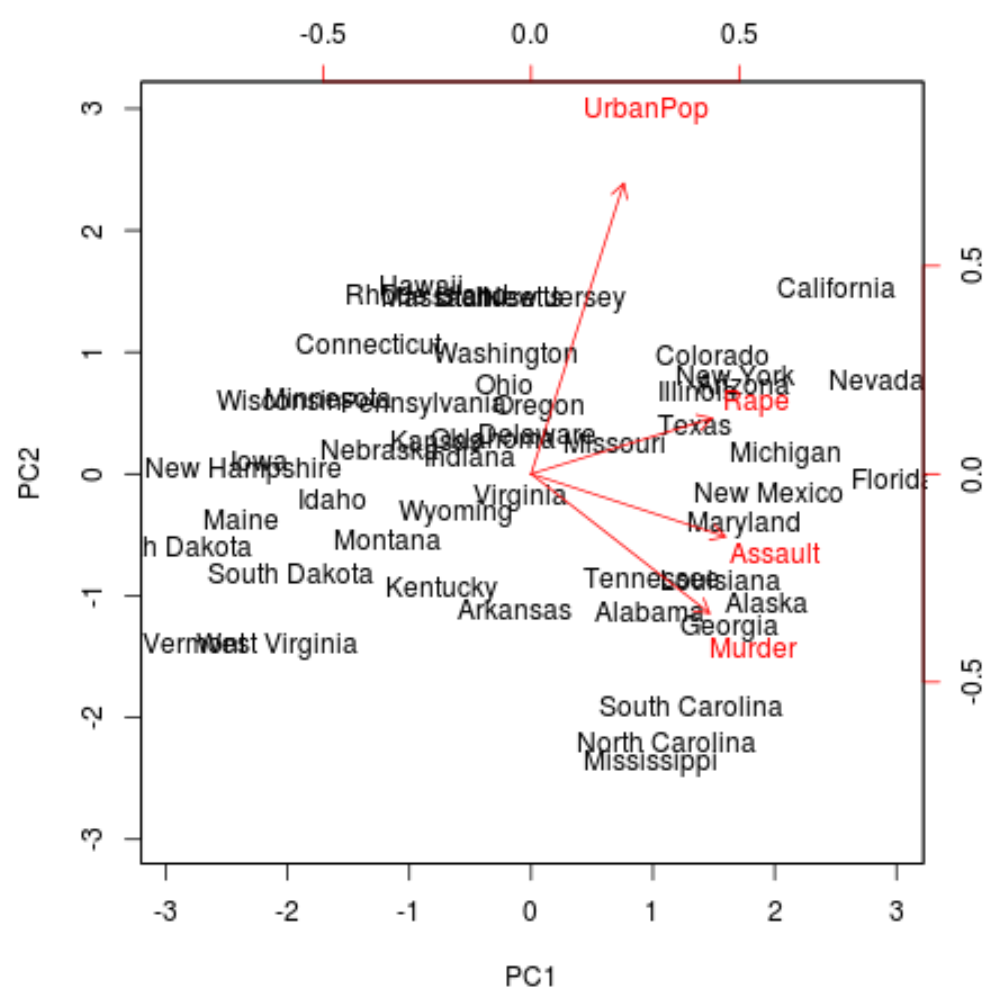
Dari plot tersebut kita dapat melihat masing-masing dari 50 negara bagian direpresentasikan dalam ruang dua dimensi sederhana.
Negara-negara yang berdekatan pada grafik memiliki pola data yang mirip dengan variabel dalam kumpulan data asli.
Kita juga dapat melihat bahwa beberapa negara bagian lebih terkait erat dengan kejahatan tertentu dibandingkan negara bagian lainnya. Misalnya, Georgia adalah negara bagian yang paling dekat dengan variabel Pembunuhan dalam plot.
Jika kita melihat negara bagian dengan tingkat pembunuhan tertinggi dalam kumpulan data asli, kita dapat melihat bahwa Georgia sebenarnya menduduki peringkat teratas:
#display states with highest murder rates in original dataset head(USArrests[ order (-USArrests$Murder),]) Murder Assault UrbanPop Rape Georgia 17.4 211 60 25.8 Mississippi 16.1 259 44 17.1 Florida 15.4 335 80 31.9 Louisiana 15.4 249 66 22.2 South Carolina 14.4 279 48 22.5 Alabama 13.2 236 58 21.2
Langkah 4: Temukan varians yang dijelaskan oleh masing-masing komponen utama
Kita dapat menggunakan kode berikut untuk menghitung total varians dalam kumpulan data asli yang dijelaskan oleh masing-masing komponen utama:
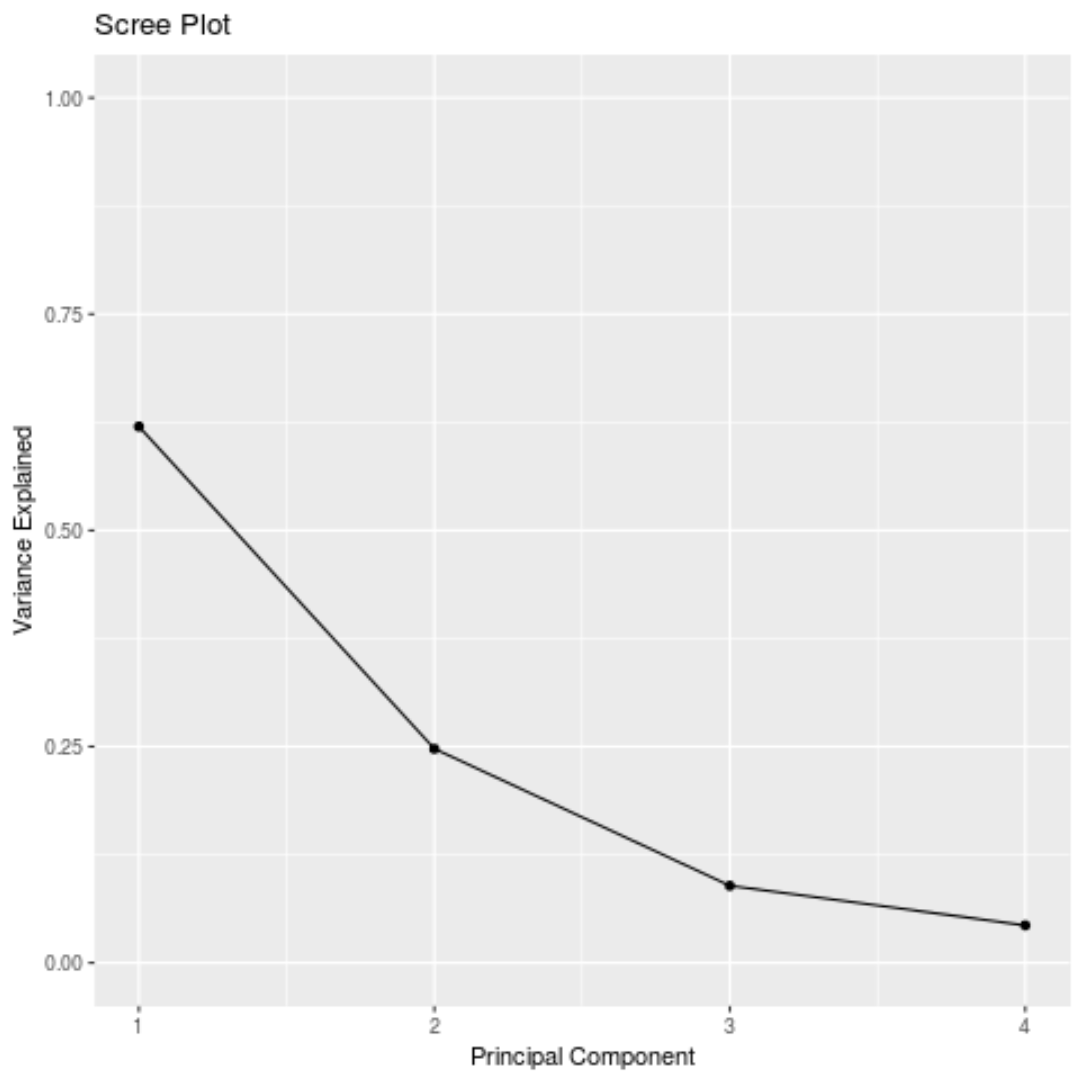
#calculate total variance explained by each principal component results$sdev^2 / sum (results$sdev^2) [1] 0.62006039 0.24744129 0.08914080 0.04335752
Dari hasilnya kita dapat mengamati hal-hal berikut:
- Komponen utama pertama menjelaskan 62% dari total varians dalam dataset.
- Komponen utama kedua menjelaskan 24,7% dari total varians dalam dataset.
- Komponen utama ketiga menjelaskan 8,9% dari total varians dalam dataset.
- Komponen utama keempat menjelaskan 4,3% dari total varians dalam dataset.
Jadi, dua komponen utama pertama menjelaskan sebagian besar total varians dalam data.
Hal ini merupakan pertanda baik karena biplot sebelumnya memproyeksikan setiap observasi dari data asli ke dalam scatterplot yang hanya memperhitungkan dua komponen utama pertama.
Oleh karena itu, valid untuk memeriksa pola dalam biplot untuk mengidentifikasi keadaan yang mirip satu sama lain.
Kita juga dapat membuat scree plot – grafik yang menampilkan total varians yang dijelaskan oleh setiap komponen utama – untuk memvisualisasikan hasil PCA:
#calculate total variance explained by each principal component var_explained = results$sdev^2 / sum (results$sdev^2) #create scree plot qplot(c(1:4), var_explained) + geom_line() + xlab(" Principal Component ") + ylab(" Variance Explained ") + ggtitle(" Scree Plot ") + ylim(0, 1)
Analisis komponen utama dalam praktiknya
Dalam praktiknya, PCA paling sering digunakan karena dua alasan:
1. Analisis Data Eksplorasi – Kami menggunakan PCA saat pertama kali menjelajahi kumpulan data dan ingin memahami observasi mana dalam data yang paling mirip satu sama lain.
2. Regresi Komponen Utama – Kita juga dapat menggunakan PCA untuk menghitung komponen utama yang kemudian dapat digunakan dalam regresi komponen utama . Regresi jenis ini sering digunakan ketika terjadi multikolinearitas antar prediktor dalam suatu kumpulan data.
Kode R lengkap yang digunakan dalam tutorial ini dapat ditemukan di sini .