Cara melakukan nested anova di r (langkah demi langkah)

ANOVA bersarang adalah jenis ANOVA (“analisis varians”) di mana setidaknya satu faktor disarangkan ke dalam faktor lain.

Misalnya, seorang peneliti ingin mengetahui apakah tiga jenis pupuk menghasilkan tingkat pertumbuhan tanaman yang berbeda.

Untuk mengujinya, tiga teknisi berbeda masing-masing menaburkan pupuk A pada empat tanaman, tiga teknisi lainnya masing-masing menaburkan pupuk B pada empat tanaman, dan tiga teknisi lainnya masing-masing menaburkan pupuk C pada empat tanaman.

Dalam skenario ini, variabel responnya adalah pertumbuhan tanaman dan kedua faktornya adalah teknisi dan pupuk. Ternyata teknisi itu terletak di dalam pupuk:

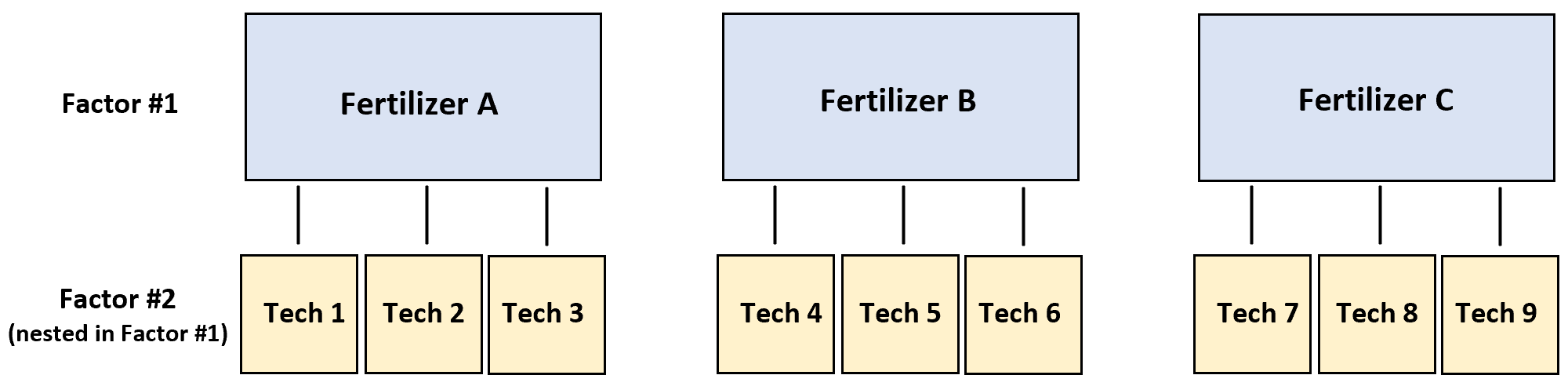
Contoh langkah demi langkah berikut menunjukkan cara melakukan ANOVA bersarang ini di R.

Langkah 1: Buat datanya

Pertama, mari buat bingkai data untuk menampung data kita di R:

 #create data
df <- data. frame (growth=c(13, 16, 16, 12, 15, 16, 19, 16, 15, 15, 12, 15,
                          19, 19, 20, 22, 23, 18, 16, 18, 19, 20, 21, 21,
                          21, 23, 24, 22, 25, 20, 20, 22, 24, 22, 25, 26),
                 fertilizer=c(rep(c(' A ', ' B ', ' C '), each= 12 )),
                 tech=c(rep(1:9, each= 4 )))

#view first six rows of data
head(df)

  growth fertilizer tech
1 13 A 1
2 16 A 1
3 16 A 1
4 12 A 1
5 15 A 2
6 16 A 2

Langkah 2: Sesuaikan ANOVA Bersarang

Kita dapat menggunakan sintaks berikut untuk menyesuaikan ANOVA bersarang di R:

aov(jawaban ~ faktor A / faktor B)

Emas:

• respon: variabel respon
• faktor A: faktor pertama
• faktor B: faktor kedua yang bersarang di faktor pertama

Kode berikut menunjukkan cara menyesuaikan ANOVA bersarang untuk kumpulan data kami:

 #fit nested ANOVA
nest <- aov(df$growth ~ df$fertilizer / factor(df$tech))

#view summary of nested ANOVA
summary(nest)

                              Df Sum Sq Mean Sq F value Pr(>F)    
df$fertilizer 2 372.7 186.33 53.238 4.27e-10 ***
df$fertilizer:factor(df$tech) 6 31.8 5.31 1.516 0.211    
Residuals 27 94.5 3.50                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Langkah 3: Tafsirkan hasilnya

Kita dapat melihat kolom p-value untuk menentukan apakah setiap faktor mempunyai pengaruh signifikan secara statistik terhadap pertumbuhan tanaman atau tidak.

Dari tabel di atas terlihat bahwa pupuk mempunyai pengaruh yang signifikan secara statistik terhadap pertumbuhan tanaman (p-value < 0,05), namun teknisi tidak (p-value = 0,211).

Hal ini menunjukkan bahwa jika kita ingin meningkatkan pertumbuhan tanaman, kita perlu fokus pada pupuk yang digunakan dibandingkan pada teknisi individu yang mengaplikasikan pupuk tersebut.

Langkah 4: Visualisasikan hasilnya

Terakhir, kita dapat menggunakan plot kotak untuk memvisualisasikan distribusi pertumbuhan tanaman berdasarkan pupuk dan teknisi:

 #load ggplot2 data visualization package
library (ggplot2)

#create boxplots to visualize plant growth
ggplot(df, aes (x=factor(tech), y=growth, fill=fertilizer)) +
  geom_boxplot()

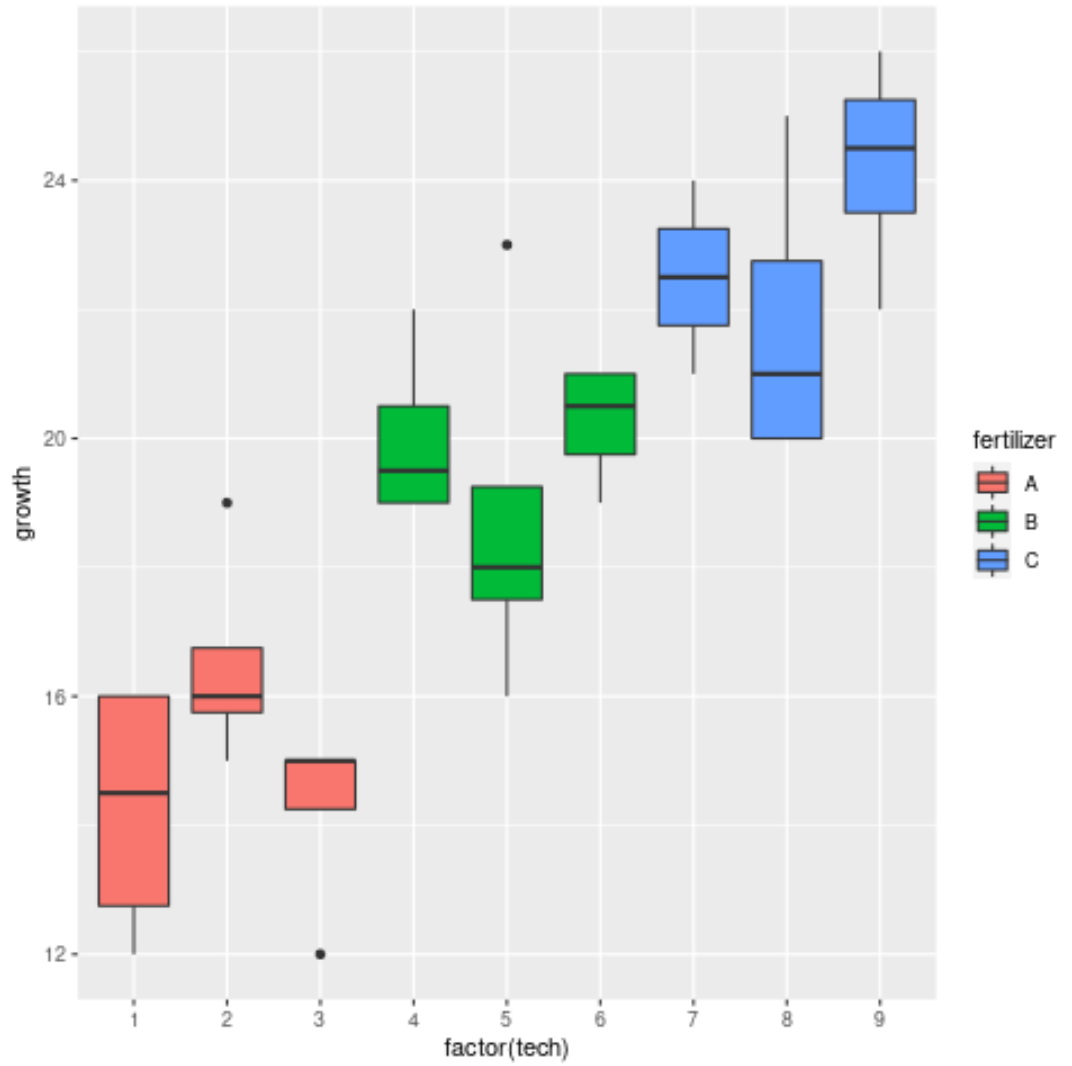
Grafik tersebut menunjukkan bahwa terdapat variasi pertumbuhan yang signifikan antara ketiga pupuk yang berbeda, namun variasi antar teknisi dalam setiap kelompok pupuk tidak terlalu besar.

Hal ini tampaknya sesuai dengan hasil ANOVA tersarang dan menegaskan bahwa pupuk mempunyai pengaruh yang signifikan terhadap pertumbuhan tanaman, namun teknisi secara individu tidak.

Sumber daya tambahan

Bagaimana melakukan ANOVA satu arah di R
Cara melakukan ANOVA dua arah di R
Bagaimana melakukan pengukuran berulang ANOVA di R