Cara melakukan anova dua arah secara manual

ANOVA dua arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen yang dibagi menjadi dua faktor.

Tutorial ini menjelaskan cara melakukan ANOVA dua arah secara manual.

Contoh: ANOVA dua arah manual

Misalkan seorang ahli botani ingin mengetahui apakah pertumbuhan tanaman dipengaruhi oleh paparan sinar matahari dan frekuensi penyiraman. Dia menanam 40 benih dan membiarkannya tumbuh selama sebulan dalam kondisi paparan sinar matahari dan frekuensi penyiraman yang berbeda.

Setelah sebulan, dia mencatat tinggi setiap tanaman. Hasilnya ditunjukkan di bawah ini:

Pada tabel di atas kita melihat lima tanaman ditanam pada setiap kombinasi kondisi.

Misalnya, lima tanaman ditanam dengan penyiraman setiap hari dan tanpa sinar matahari dan tingginya setelah dua bulan adalah 4,8 inci, 4,4 inci, 3,2 inci, 3,9 inci, dan 4,4 inci:

Kita dapat menggunakan langkah-langkah berikut untuk melakukan ANOVA dua arah:

Langkah 1: Hitung jumlah kuadrat faktor pertama (frekuensi penyiraman)

Pertama, kita akan menghitung tinggi rata-rata keseluruhan dari 40 tanaman:

Rata-rata keseluruhan = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Selanjutnya, kita menghitung tinggi rata-rata semua tanaman yang disiram setiap hari:

Rata-rata harian = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155

Selanjutnya kita hitung rata-rata tinggi seluruh tanaman yang disiram setiap minggunya:

Rata-rata mingguan = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15

Selanjutnya, kita akan menghitung jumlah kuadrat faktor “frekuensi penyiraman” menggunakan rumus berikut:

Σn(X _j – X ..) ²

Emas:

• n : ukuran sampel kelompok j
• Σ : simbol Yunani yang berarti “jumlah”
• X _j : rata-rata kelompok j
• X .. : rata-rata yang besar

Dalam contoh kita, kita menghitung jumlah kuadrat faktor “frekuensi penyiraman” sebagai berikut: 20(5.155-5.1525) ² + 20(5.15-5.1525) ² = 0.00025

Langkah 2: Hitung jumlah kuadrat faktor kedua (paparan sinar matahari)

Pertama, kita akan menghitung tinggi rata-rata keseluruhan dari 40 tanaman:

Rata-rata keseluruhan = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Selanjutnya kita akan menghitung rata-rata tinggi semua tanaman yang tidak terkena sinar matahari:

Rata-rata tanpa matahari = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07

Kami akan mengulangi perhitungan ini untuk mencari tinggi rata-rata tanaman yang terkena berbagai paparan sinar matahari:

• Rata-rata sinar matahari rendah = 5,1
• Rata-rata sinar matahari rata-rata = 5,89
• Rata-rata tinggi sinar matahari = 5,55

Selanjutnya, kita akan menghitung jumlah kuadrat faktor “paparan sinar matahari” menggunakan rumus berikut:

Σn(X _j – X ..) ²

Emas:

• n : ukuran sampel kelompok j
• Σ : simbol Yunani yang berarti “jumlah”
• X _j : rata-rata kelompok j
• X .. : rata-rata yang besar

Dalam contoh kita, kita menghitung jumlah kuadrat faktor “paparan sinar matahari” sebagai berikut: 10(4.07-5.1525) ² + 10(5.1-5.1525) ² + 10(5.89 -5.1525) ² + 10(5.55-5.1525) ² = 18,76475

Langkah 3: Hitung jumlah kuadrat di dalamnya (kesalahan)

Selanjutnya, kita akan menghitung jumlah kuadrat dengan mengambil jumlah kuadrat selisih antara setiap kombinasi faktor dan tinggi tanaman individu.

Misalnya rata-rata tinggi seluruh tanaman yang disiram setiap hari tanpa terkena sinar matahari adalah 4,14. Kita kemudian dapat menghitung jumlah kuadrat selisih masing-masing tanaman sebagai berikut:

• SS untuk penyiraman harian dan tanpa sinar matahari: (4.8-4.14) ² + (4.4-4.14) ² + (3.2-4.14) ² + (3.9-4.14) ² + (4.4-4.14) ² = 1.512

Kita dapat mengulangi proses ini untuk setiap kombinasi faktor:

• SS untuk penyiraman harian dan sinar matahari rendah: 0,928
• SS untuk penyiraman harian dan rata-rata sinar matahari: 1,788
• SS untuk penyiraman harian dan sinar matahari yang kuat: 1.648
• SS untuk penyiraman mingguan tanpa sinar matahari: 0,34
• SS untuk penyiraman mingguan dan sinar matahari rendah: 0,548
• SS untuk penyiraman mingguan dan rata-rata sinar matahari: 0,652
• SS untuk penyiraman mingguan dan sinar matahari yang kuat: 1.268

Kita kemudian dapat mengambil jumlah semua nilai ini untuk menemukan jumlah kuadrat di dalamnya (kesalahan):

Jumlah kuadrat di dalamnya = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684

Langkah 4: Hitung jumlah total persegi

Kemudian kita dapat menghitung jumlah total kuadrat dengan mengambil jumlah selisih antara tinggi masing-masing tanaman dan rata-rata keseluruhannya:

Jumlah kuadrat = (4,8 – 5,1525) ² + (5 – 5,1525) ² + … + (5,5 – 5,1525) ² = 28,45975

Langkah 5: Hitung jumlah interaksi kuadrat

Selanjutnya kita akan menghitung jumlah interaksi kuadrat dengan menggunakan rumus berikut:

• Interaksi SS = SS Total – SS Faktor 1 – SS Faktor 2 – SS Interior
• Interaksi SS = 28.45975 – 0.00025 – 18.76475 – 8.684
• Interaksi SS = 1,01075

Langkah 6: Lengkapi tabel ANOVA

Terakhir, kita akan mengisi nilai dari tabel ANOVA dua arah:

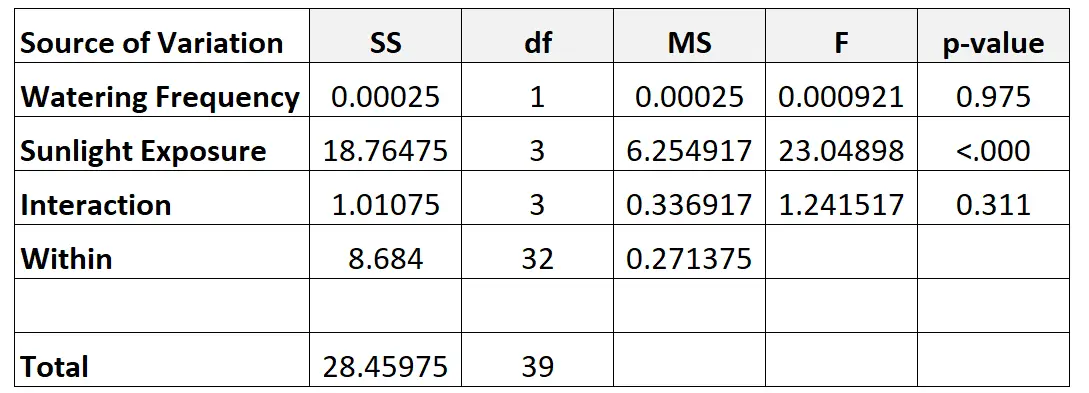
Inilah cara kami menghitung angka-angka berbeda dalam tabel:

• df Frekuensi penyiraman : d-1 = 2-1 = 1
• df Paparan sinar matahari : k-1 = 4-1 = 3
• dfInteraksi : (j-1)*(k-1) = 1*3 = 3
• df Masuk : n – (j*k) = 40 – (2*4) = 32
• jumlah df: n-1 = 40-1 = 39
• MS: SS/DF
• Frekuensi penyiraman F : frekuensi penyiraman MS/MS dalam ruangan
• F Paparan sinar matahari : MS / MS paparan sinar matahari di dalam ruangan
• Interaksi F : Interaksi MS/MS Dalam
• nilai p frekuensi penyiraman : Nilai p yang sesuai dengan nilai F sebesar 0,000921 dengan pembilang df = 1 dan penyebut df = 32
• Nilai p paparan sinar matahari : nilai p yang sesuai dengan nilai F 23,04898 dengan pembilang df = 3 dan penyebut df = 32
• interaksi nilai p : Nilai p yang sesuai dengan nilai F sebesar 1,241517 dengan pembilang df = 3 dan penyebut df = 32

Catatan #1: n = jumlah pengamatan, j = jumlah level frekuensi penyiraman, k = jumlah level paparan sinar matahari.

Catatan #2 : Nilai p yang sesuai dengan nilai F dihitung menggunakan kalkulator distribusi F.

Langkah 7: Interpretasikan hasilnya

Berikut ini dapat kita amati dari tabel ANOVA:

• Nilai p interaksi antara frekuensi penyiraman dan paparan sinar matahari adalah 0,311 . Hal ini tidak signifikan secara statistik pada α = 0,05.
• Nilai p untuk frekuensi penyiraman adalah 0,975 . Hal ini tidak signifikan secara statistik pada α = 0,05.
• Nilai p untuk paparan sinar matahari adalah <0,000 . Hal ini signifikan secara statistik pada α = 0,05.

Hasil ini menunjukkan bahwa paparan sinar matahari merupakan satu-satunya faktor yang mempunyai pengaruh signifikan secara statistik terhadap tinggi tanaman.

Dan karena tidak ada efek interaksi, maka efek paparan sinar matahari konsisten pada setiap tingkat frekuensi penyiraman.

Sederhananya, apakah tanaman disiram setiap hari atau setiap minggu tidak berdampak pada pengaruh paparan sinar matahari terhadap tanaman.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang ANOVA:

Cara melakukan ANOVA satu arah secara manual
Cara Melakukan ANOVA Pengukuran Berulang Secara Manual
Panduan Lengkap: Cara Melaporkan Hasil ANOVA Dua Arah