Anova satu arah: pengertian, rumus dan contoh
ANOVA satu arah (“analisis varians”) membandingkan rata-rata dari tiga atau lebih kelompok independen untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata populasi yang bersangkutan.
Tutorial ini menjelaskan hal berikut:
- Motivasi untuk melakukan ANOVA satu arah.
- Asumsi yang harus dipenuhi untuk melakukan ANOVA satu arah.
- Proses untuk melakukan ANOVA satu arah.
- Contoh cara melakukan ANOVA satu arah.
ANOVA satu arah: motivasi
Misalkan kita ingin mengetahui apakah tiga program persiapan ujian yang berbeda menghasilkan nilai rata-rata yang berbeda pada ujian masuk perguruan tinggi. Karena terdapat jutaan siswa sekolah menengah di seluruh negeri, akan terlalu memakan waktu dan mahal untuk menemui setiap siswa dan membiarkan mereka menggunakan salah satu program persiapan ujian.
Sebaliknya, kita dapat memilih tiga sampel acak yang terdiri dari 100 siswa dari populasi dan mengizinkan setiap sampel menggunakan salah satu dari tiga program persiapan ujian untuk mempersiapkan ujian. Kemudian kami dapat mencatat nilai setiap siswa setelah mereka mengikuti ujian.
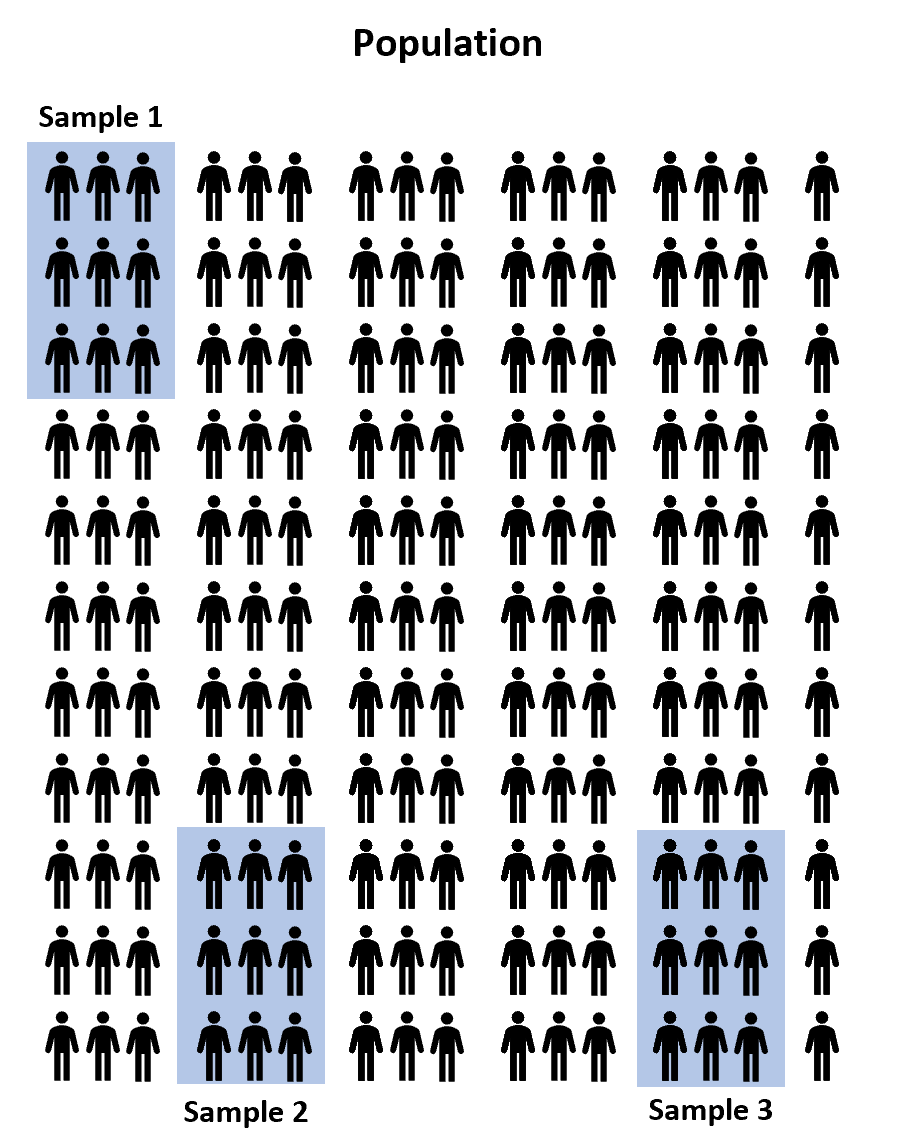
Namun, dapat dipastikan bahwa rata-rata nilai ujian antara ketiga sampel tersebut setidaknya akan sedikit berbeda. Pertanyaannya adalah apakah perbedaan ini signifikan secara statistik . Untungnya, ANOVA satu arah memungkinkan kita menjawab pertanyaan ini.
ANOVA satu arah: asumsi
Agar hasil ANOVA satu arah valid, asumsi berikut harus dipenuhi:
1. Normalitas – Setiap sampel diambil dari populasi yang berdistribusi normal.
2. Varians yang sama – Varians dari populasi yang dijadikan sampel adalah sama. Anda dapat menggunakan uji Bartlett untuk menguji hipotesis ini.
3. Independensi – Pengamatan dalam setiap kelompok tidak bergantung satu sama lain dan pengamatan dalam kelompok diperoleh dengan pengambilan sampel secara acak.
Baca artikel ini untuk detail lebih lanjut tentang cara memverifikasi asumsi ini.
ANOVA satu arah: prosesnya
ANOVA satu arah menggunakan hipotesis nol dan hipotesis alternatif berikut:
- H 0 (hipotesis nol): μ 1 = μ 2 = μ 3 = … = μ k (semua rata-rata populasi adalah sama)
- H 1 (hipotesis alternatif): setidaknya satu mean populasi berbeda istirahat
Anda biasanya akan menggunakan beberapa perangkat lunak statistik (seperti R, Excel, Stata, SPSS, dll.) untuk melakukan ANOVA satu arah karena membosankan jika dilakukan secara manual.
Terlepas dari perangkat lunak yang Anda gunakan, Anda akan menerima tabel berikut sebagai output:
| Sumber | Jumlah kuadrat (SS) | df | Kuadrat rata-rata (MS) | F | P |
|---|---|---|---|---|---|
| Perlakuan | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Kesalahan | ESS | df e | UMK | ||
| Total | K3 | df t |
Emas:
- SSR: regresi jumlah kuadrat
- SSE: jumlah kesalahan kuadrat
- SST: jumlah total kuadrat (SST = SSR + SSE)
- df r : derajat kebebasan regresi (df r = k-1)
- df e : derajat kebebasan kesalahan (df e = nk)
- df t : derajat kebebasan total (df t = n-1)
- k: jumlah total kelompok
- n : jumlah observasi
- MSR: regresi kuadrat rata-rata (MSR = SSR/df r )
- MSE: kesalahan kuadrat rata-rata (MSE = SSE/df e )
- F: Statistik uji F (F = MSR/MSE)
- p: Nilai p yang sesuai dengan F dfr, dfe
Jika nilai p lebih kecil dari tingkat signifikansi yang dipilih (misalnya 0,05), maka Anda dapat menolak hipotesis nol dan menyimpulkan bahwa setidaknya salah satu mean populasi berbeda dengan mean populasi lainnya.
Catatan: Jika Anda menolak hipotesis nol, ini menunjukkan bahwa setidaknya salah satu mean populasi berbeda dari yang lain, namun tabel ANOVA tidak menentukan mean populasi mana yang berbeda. Untuk menentukan hal ini, Anda perlu melakukan pengujian post hoc , yang juga disebut pengujian “perbandingan berganda”.
ANOVA satu arah: contoh
Misalkan kita ingin mengetahui apakah tiga program persiapan ujian yang berbeda menghasilkan nilai rata-rata yang berbeda pada ujian tertentu. Untuk mengujinya, kami merekrut 30 siswa untuk berpartisipasi dalam penelitian dan membagi mereka menjadi tiga kelompok.
Siswa di setiap kelompok secara acak ditugaskan untuk menggunakan salah satu dari tiga program persiapan ujian selama tiga minggu berikutnya untuk mempersiapkan ujian. Pada akhir tiga minggu, semua siswa mengikuti ujian yang sama.
Hasil ujian masing-masing kelompok ditunjukkan di bawah ini:

Untuk melakukan ANOVA satu arah pada data ini, kami akan menggunakan Kalkulator ANOVA Statistik Satu Arah dengan input sebagai berikut:

Dari tabel keluaran, kita melihat bahwa statistik uji F adalah 2,358 dan nilai p yang sesuai adalah 0,11385 .

Karena nilai p ini tidak kurang dari 0,05, kita gagal menolak hipotesis nol.
Artinya, kami tidak memiliki cukup bukti untuk mengatakan bahwa terdapat perbedaan yang signifikan secara statistik antara rata-rata nilai ujian ketiga kelompok.
Sumber daya tambahan
Artikel berikut menjelaskan cara melakukan ANOVA satu arah menggunakan perangkat lunak statistik yang berbeda:
Bagaimana Melakukan ANOVA Satu Arah di Excel
Bagaimana melakukan ANOVA satu arah di R
Cara Melakukan ANOVA Satu Arah dengan Python
Cara melakukan ANOVA satu arah di SAS
Cara Melakukan ANOVA Satu Arah di SPSS
Cara melakukan ANOVA satu arah di Stata
Cara Melakukan ANOVA Satu Arah pada Kalkulator TI-84
Kalkulator ANOVA Satu Arah Online