Cara melakukan anova satu arah di spss

ANOVA satu arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen.

Jenis pengujian ini disebut ANOVA satu arah karena kami menganalisis dampak variabel prediktor terhadap variabel respon.

Jika kita tertarik pada dampak dua variabel prediktor terhadap variabel respon, kita dapat melakukan ANOVA dua arah .

Tutorial ini menjelaskan cara melakukan ANOVA satu arah di SPSS.

Contoh: ANOVA satu arah di SPSS

Misalkan seorang peneliti merekrut 30 siswa untuk berpartisipasi dalam suatu penelitian. Siswa secara acak ditugaskan untuk menggunakan salah satu dari tiga teknik belajar pada bulan berikutnya untuk mempersiapkan ujian. Pada akhir bulan, semua siswa mengikuti tes yang sama.

Hasil tes siswa ditunjukkan di bawah ini:

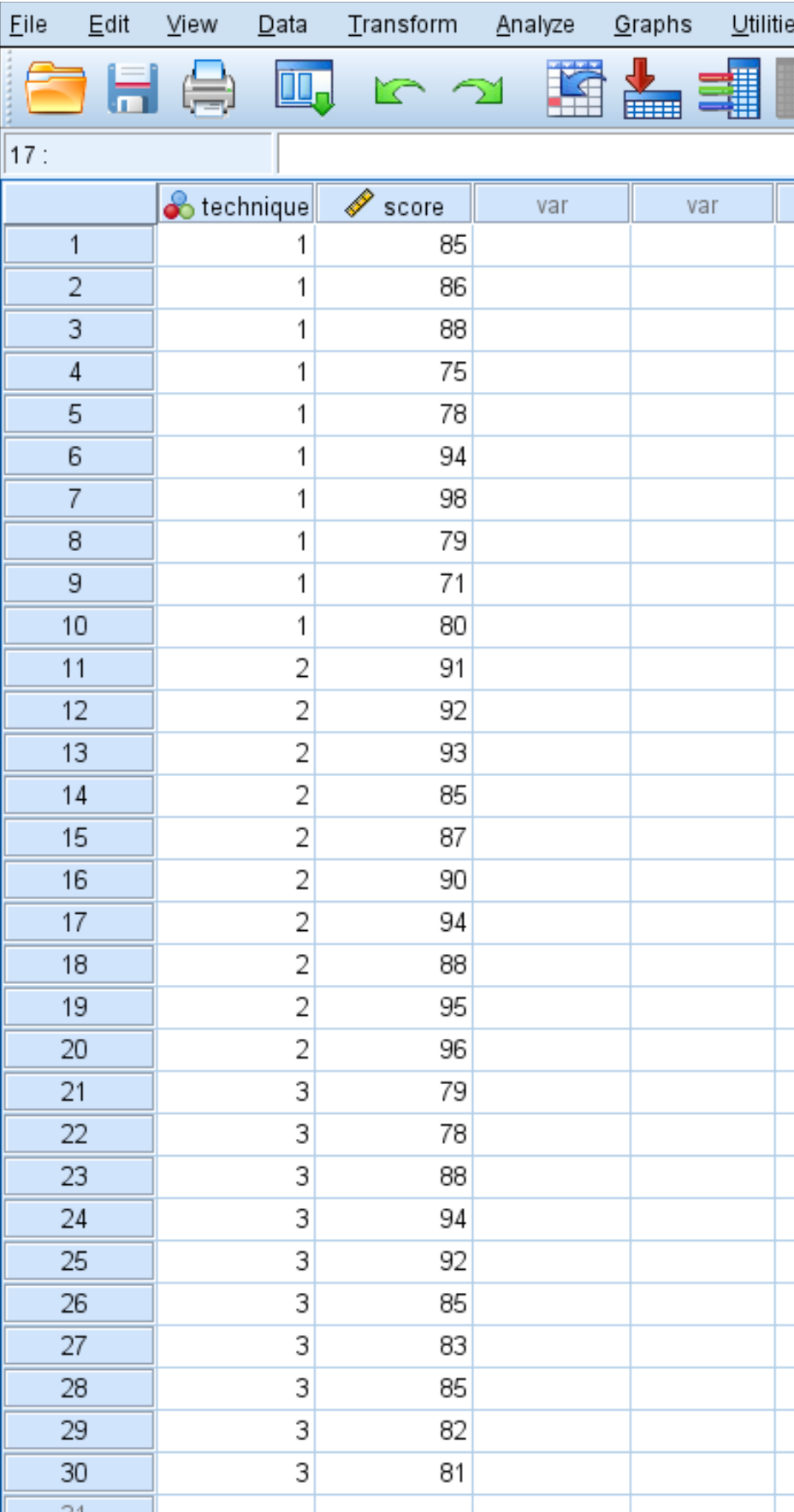
Gunakan langkah-langkah berikut untuk melakukan ANOVA satu arah untuk menentukan apakah skor rata-rata sama di ketiga kelompok.

Langkah 1: Visualisasikan datanya.

Pertama, kita akan membuat plot kotak untuk memvisualisasikan distribusi nilai ujian untuk masing-masing dari ketiga teknik pembelajaran. Klik tab Bagan , lalu klik Pembuat Bagan .

Pilih Boxplot di jendela Pilih dari:. Kemudian seret bagan pertama berlabel Simple boxplot ke dalam jendela pengeditan utama. Tarik variabel teknis pada sumbu x dan skor pada sumbu y.

Lalu klik Element Properties , lalu klik Y1 Axis . Ubah nilai minimum menjadi 60. Lalu klik OK .

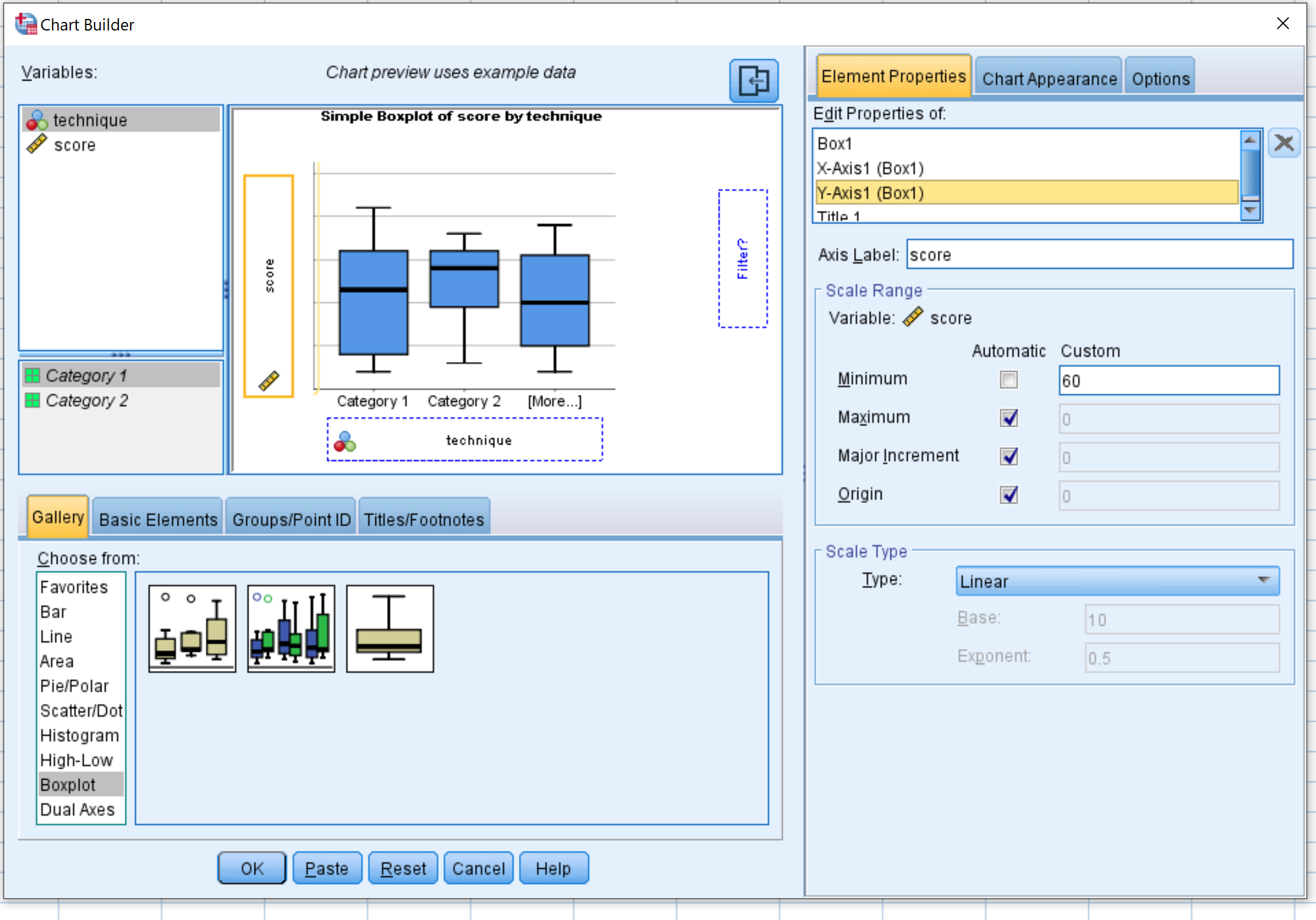
Akan muncul boxplot berikut:

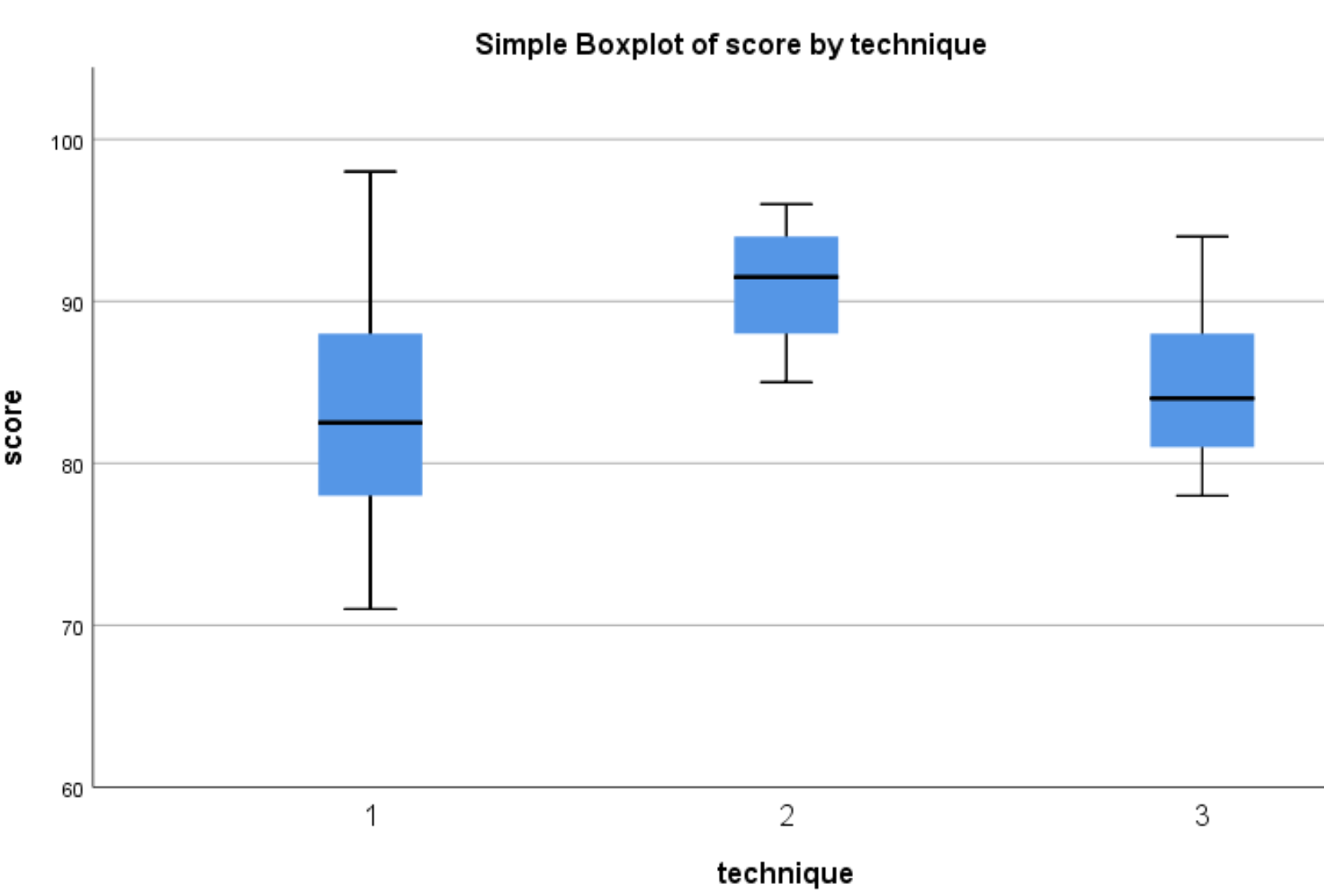
Terlihat bahwa distribusi nilai tes cenderung lebih tinggi pada siswa yang menggunakan Teknik 2 dibandingkan siswa yang menggunakan Teknik 1 dan 3. Untuk menentukan apakah perbedaan skor tersebut signifikan secara statistik, kami akan melakukan ANOVA satu arah.

Langkah 2: Lakukan ANOVA satu arah.

Klik tab Analyze , lalu Compare Means , lalu One-Way ANOVA .

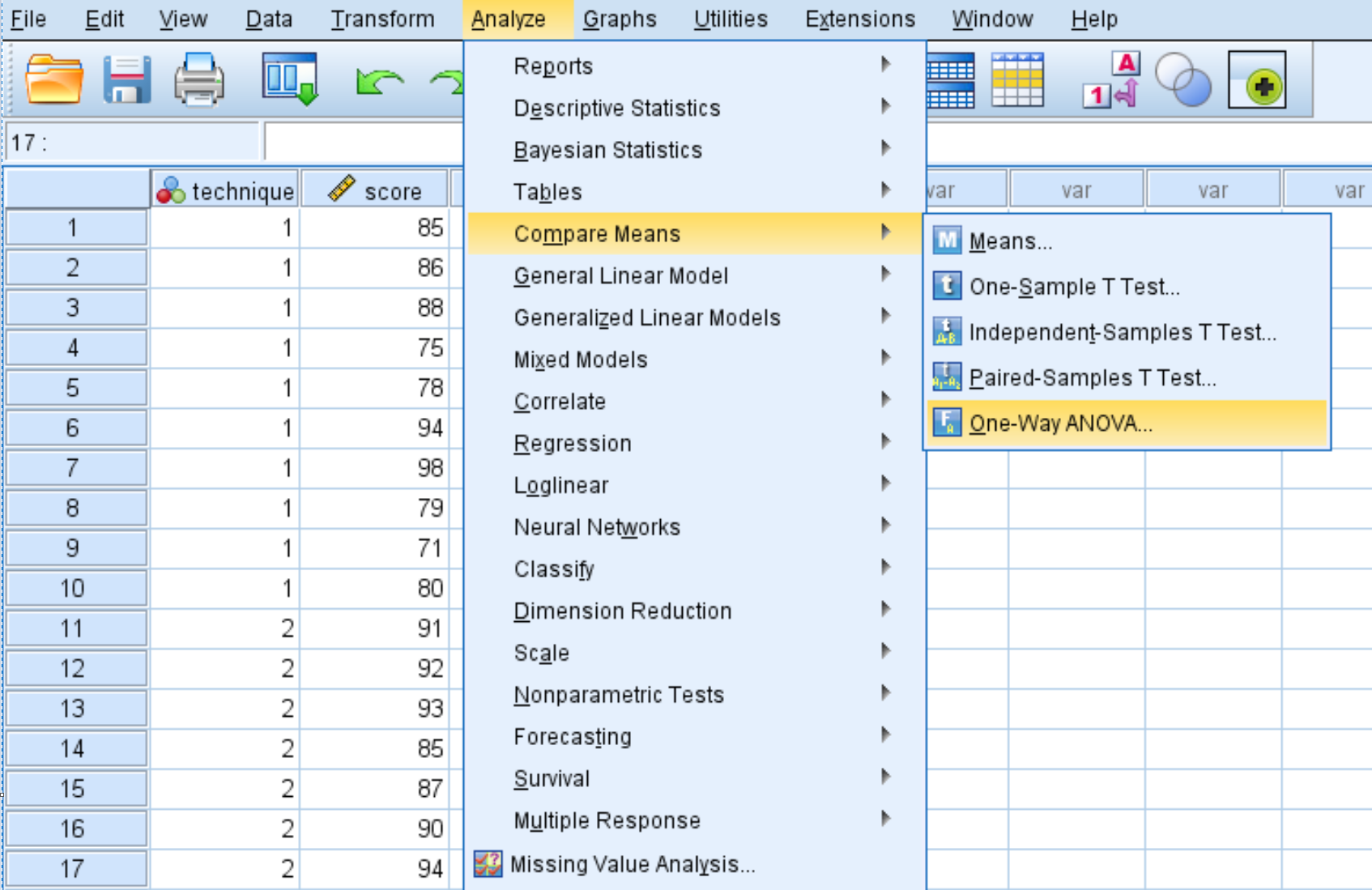
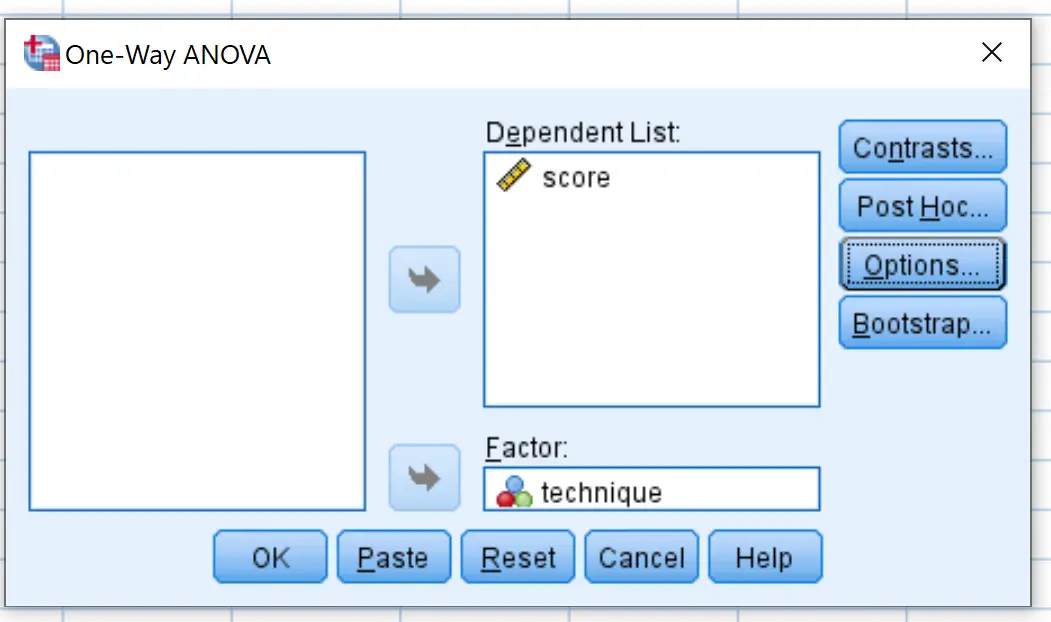
Pada jendela baru yang muncul, tempatkan skor variabel pada kotak berlabel Daftar Dependen dan teknik variabel dalam kotak berlabel Faktor.

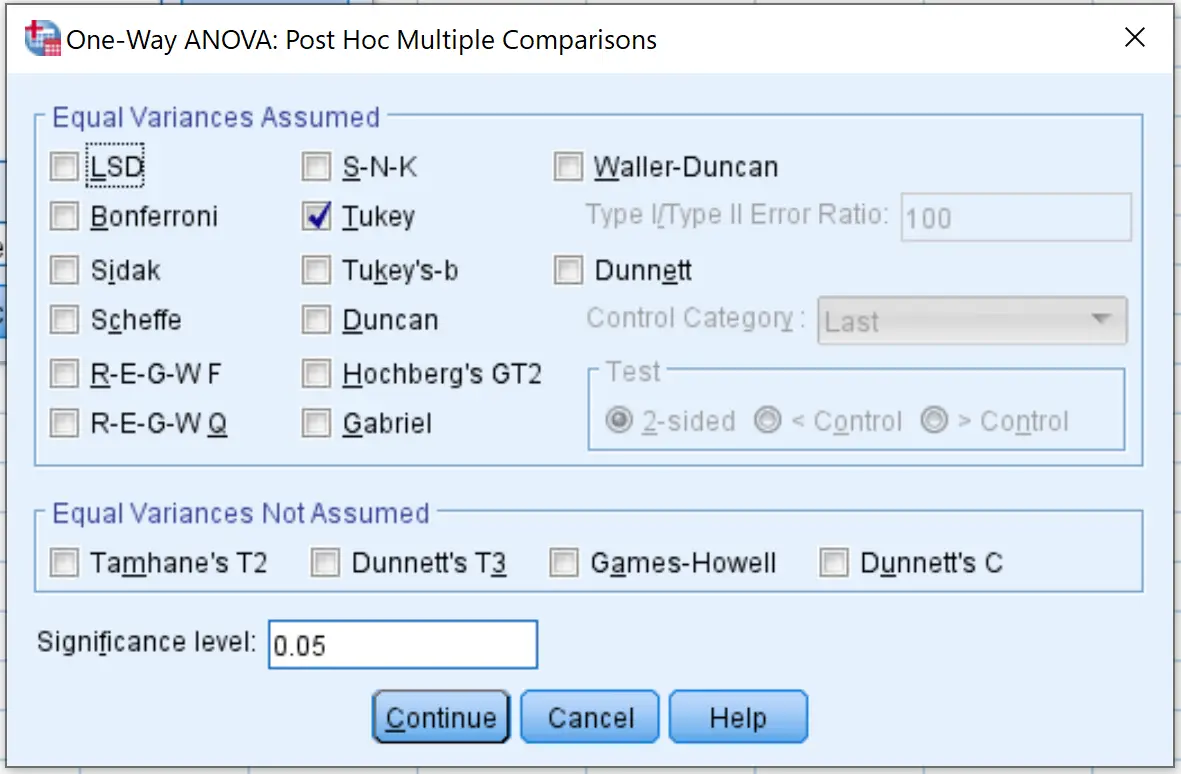
Kemudian klik Post Hoc dan centang kotak di sebelah Tukey . Lalu klik Lanjutkan .

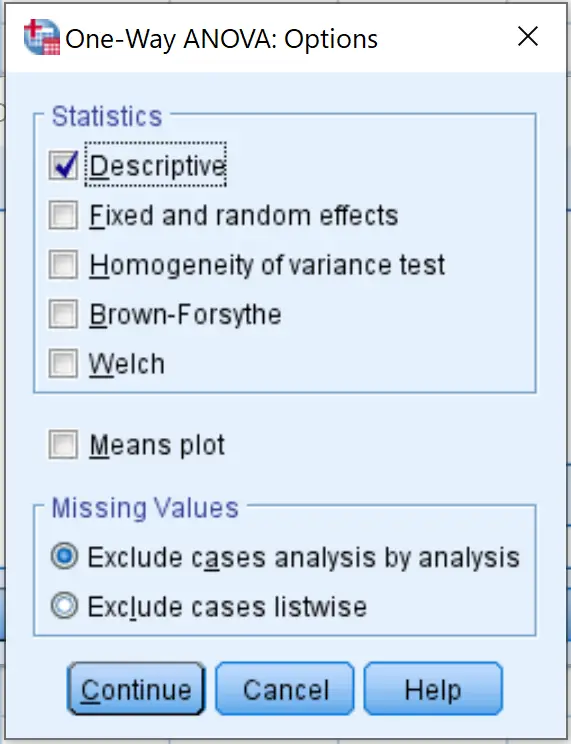
Kemudian klik Opsi dan centang kotak di sebelah Deskriptif . Lalu klik Lanjutkan .

Terakhir, klik OK .

Langkah 3: Tafsirkan hasilnya.

Setelah Anda klik OK , maka akan muncul hasil ANOVA satu arah. Berikut cara menafsirkan hasilnya:

Deskripsi tabel

Tabel ini menampilkan statistik deskriptif untuk masing-masing dari tiga kelompok dalam kumpulan data kami.

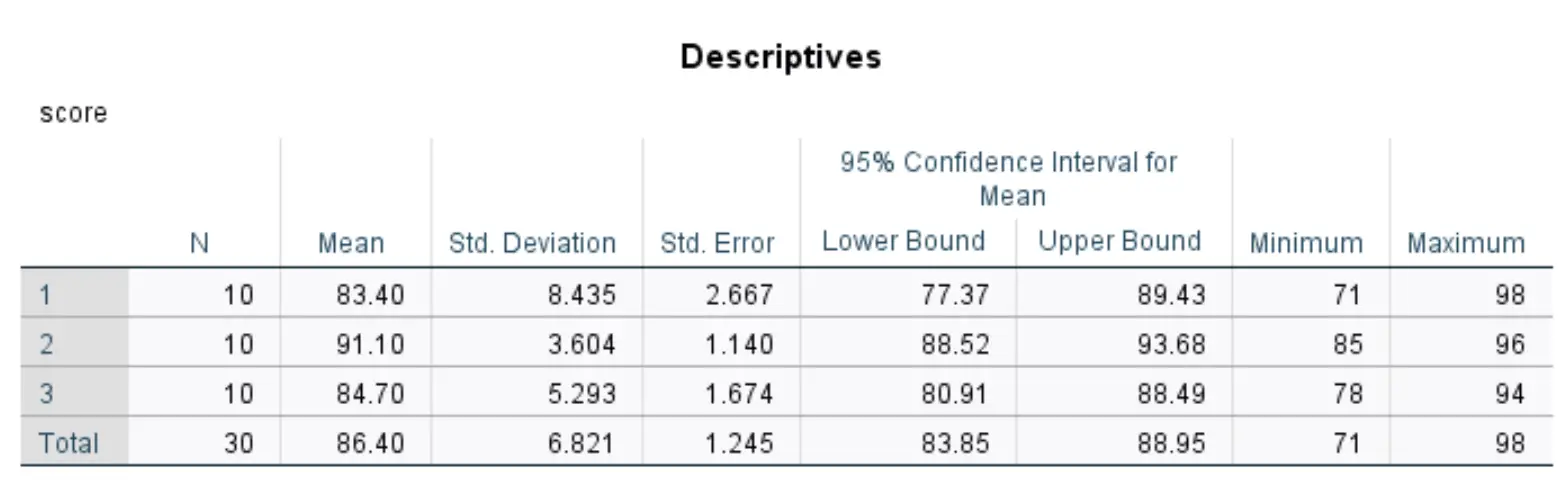
Angka-angka yang paling relevan meliputi:

• N : Banyaknya siswa dalam setiap kelompok.
• Rata-rata: Rata-rata nilai tes tiap kelompok.
• Standar. Deviasi : Standar deviasi hasil tes tiap kelompok.

tabel ANOVA

Tabel berikut menampilkan hasil ANOVA satu arah:

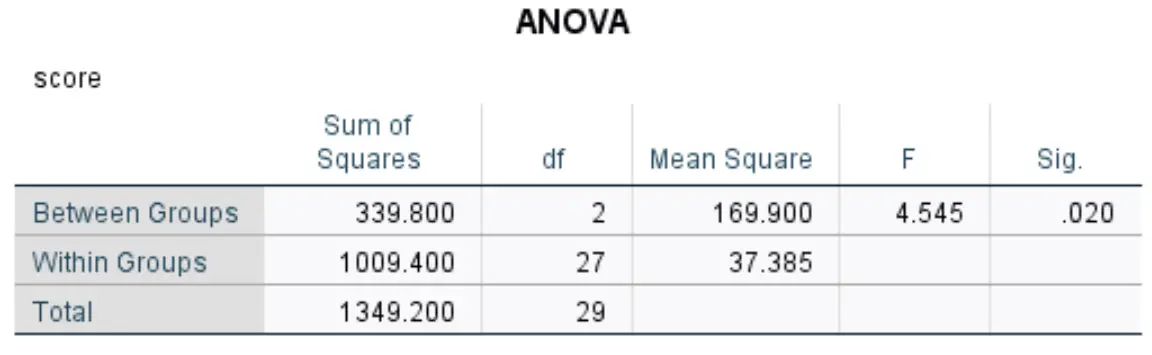
Angka-angka yang paling relevan meliputi:

• F : Statistik F keseluruhan.
• Sig: Nilai p yang sesuai dengan statistik F (4,545) dengan pembilang df (2) dan penyebut df (27). Dalam hal ini, nilai p menjadi 0,020 .

Ingatlah bahwa ANOVA satu arah menggunakan hipotesis nol dan hipotesis alternatif berikut:

• H ₀ (hipotesis nol): μ ₁ = μ ₂ = μ ₃ = … = μ _k (semua rata-rata populasi adalah sama)
• H _A (hipotesis alternatif): setidaknya satu mean populasi berbeda   istirahat

Karena nilai p tabel ANOVA kurang dari 0,05, kami memiliki cukup bukti untuk menolak hipotesis nol dan menyimpulkan bahwa setidaknya salah satu mean kelompok berbeda dari mean kelompok lainnya.

Untuk mengetahui secara pasti mean kelompok mana yang berbeda satu sama lain, kita dapat mengacu pada tabel terakhir hasil ANOVA.

Tabel perbandingan berganda

Tabel ini menampilkan beberapa perbandingan post-hoc Tukey antara ketiga kelompok. Kami terutama tertarik pada Sig. kolom, yang menampilkan nilai p untuk perbedaan rata-rata antara masing-masing kelompok:

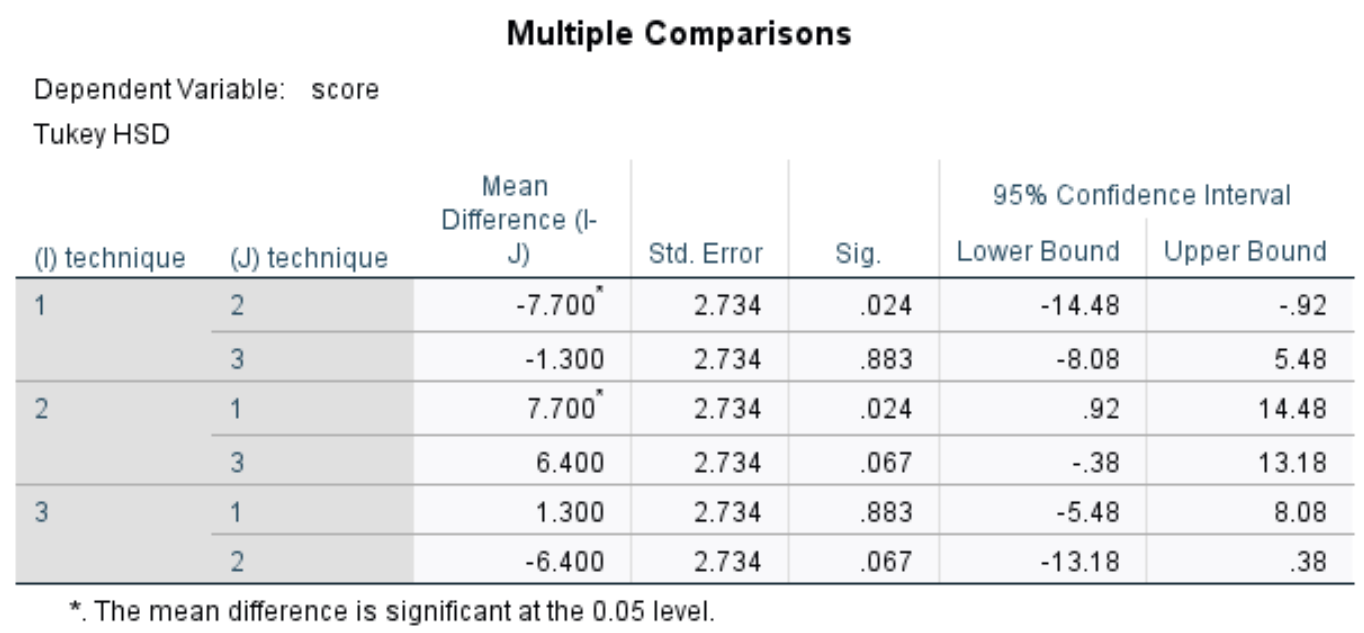
Pada tabel kita dapat melihat nilai p untuk perbandingan berikut:

• Teknik 1 lawan 2 : | nilai p = 0,024
• Teknik 1 lawan 3 | nilai p = 0,883
• Teknik 2 lawan 3 | nilai p = 0,067

Satu-satunya perbandingan kelompok dengan nilai p kurang dari 0,05 adalah antara Teknik 1 dan Teknik 2.

Hal ini menunjukkan bahwa terdapat perbedaan yang signifikan secara statistik dalam nilai rata-rata tes antara siswa yang menggunakan Teknik 1 dan siswa yang menggunakan Teknik 2.

Namun, tidak ada perbedaan yang signifikan secara statistik antara teknik 1 dan 3, maupun antara teknik 2 dan 3.

Langkah 4: Laporkan hasilnya.

Terakhir, kami dapat melaporkan hasil ANOVA satu arah. Berikut ini contoh cara melakukan ini:

ANOVA satu arah dilakukan untuk menentukan apakah tiga teknik penelitian yang berbeda menghasilkan hasil tes yang berbeda.

Sebanyak 10 siswa menggunakan masing-masing dari tiga teknik belajar selama sebulan sebelum semuanya mengikuti tes yang sama.

ANOVA satu arah menunjukkan bahwa terdapat perbedaan skor tes yang signifikan secara statistik antara setidaknya dua kelompok (F(2, 27) = 4,545, p = 0,020).

Uji Tukey untuk perbandingan berganda menunjukkan bahwa nilai rata-rata tes berbeda secara signifikan antara siswa yang menggunakan Teknik 1 dan Teknik 2 (p = 0,024, 95% CI = [-14,48, -0,92]).

Tidak ada perbedaan yang signifikan secara statistik antara skor teknik 1 dan 3 (p = 0,883) atau antara skor teknik 2 dan 3 (p = 0,067).