Bagaimana melakukan anova satu arah di excel
ANOVA satu arah (“analisis varians”) digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen.
Tutorial ini menjelaskan cara melakukan ANOVA satu arah di Excel.
Contoh: ANOVA satu arah di Excel
Misalkan seorang peneliti merekrut 30 siswa untuk berpartisipasi dalam suatu penelitian. Siswa secara acak ditugaskan untuk menggunakan salah satu dari tiga teknik belajar selama tiga minggu ke depan untuk mempersiapkan ujian. Pada akhir tiga minggu, semua siswa mengikuti tes yang sama.
Hasil tes siswa ditunjukkan di bawah ini:
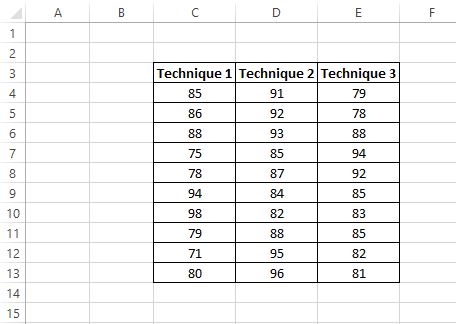
Peneliti ingin melakukan ANOVA satu arah untuk menentukan apakah skor rata-rata ketiga kelompok sama.
Untuk melakukan ANOVA satu arah di Excel, buka tab Data , lalu klik opsi Analisis Data di grup Analisis .
Jika Anda tidak melihat opsi Analisis Data , Anda harus memuat perangkat lunak Analysis ToolPak gratis terlebih dahulu.

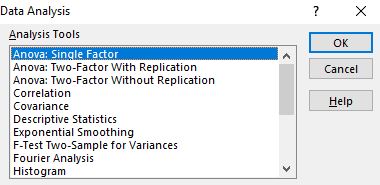
Setelah Anda mengkliknya, sebuah jendela akan muncul dengan opsi alat pindai yang berbeda. Pilih Anova: Faktor Tunggal , lalu klik OK .
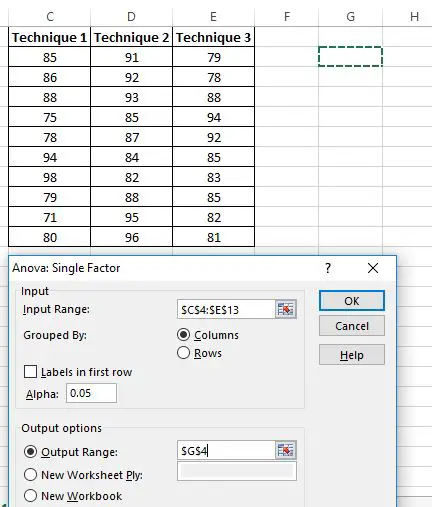
Jendela baru muncul menanyakan rentang masukan . Anda dapat menyeret kotak di sekitar data Anda atau memasukkan rentang data secara manual. Dalam hal ini, data kita ada di sel C4:E13 .
Selanjutnya, pilih level Alpha untuk ujian. Secara default, angka ini adalah 0,05. Dalam hal ini, saya akan membiarkannya pada 0,05.
Terakhir, pilih sel untuk Rentang Output , dimana hasil ANOVA satu arah akan muncul. Dalam hal ini, saya memilih sel G4 .
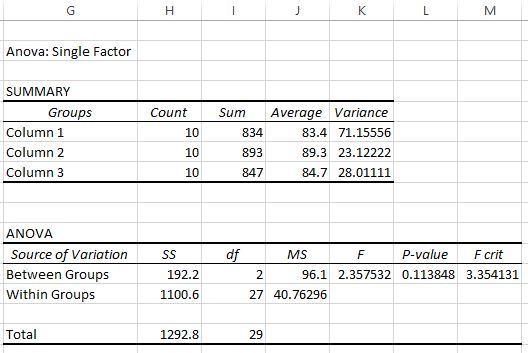
Setelah Anda klik OK , maka akan muncul hasil ANOVA satu arah:
Interpretasi hasilnya
Dua tabel ditampilkan di output. Yang pertama adalah tabel ringkasan yang menunjukkan jumlah nilai tes pada setiap kelompok, jumlah nilai tes, rata-rata nilai tes, dan varians nilai tes.
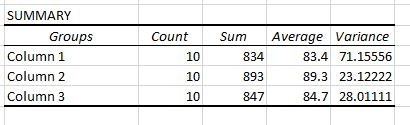
Ingatlah bahwa ANOVA satu arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga kelompok atau lebih.
Dari tabel pertama ini kita dapat melihat bahwa skor rata-rata untuk masing-masing ketiga kelompok berbeda, namun untuk mengetahui apakah perbedaan tersebut signifikan secara statistik kita perlu melihat tabel kedua.
Tabel kedua menunjukkan statistik uji F, nilai F kritis, dan nilai p:
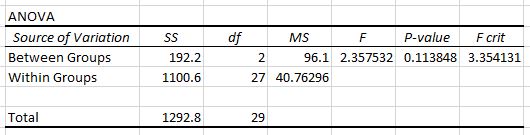
Dalam hal ini statistik uji F sebesar 2,3575 dan nilai kritis F sebesar 3,3541 . Karena statistik uji F lebih kecil dari nilai kritis F, kita tidak mempunyai cukup bukti untuk menolak hipotesis nol yang menyatakan rata-rata ketiga kelompok adalah sama.
Artinya kami tidak mempunyai bukti yang cukup untuk mengatakan bahwa terdapat perbedaan hasil tes antara ketiga teknik penelitian.
Kita juga bisa menggunakan nilai p untuk mencapai kesimpulan yang sama. Dalam hal ini, nilai p-nya adalah 0,1138 , lebih tinggi dari tingkat alfa 0,05 .
Artinya kita tidak mempunyai cukup bukti untuk menolak hipotesis nol yang menyatakan bahwa rata-rata ketiga kelompok adalah sama.
Catatan: Jika Anda menolak hipotesis nol, Anda dapat melakukanuji post hoc Tukey-Kramer untuk menentukan dengan pasti mean grup mana yang berbeda.