Anova tiga arah: definisi & contoh

ANOVA tiga arah digunakan untuk menentukan bagaimana tiga faktor berbeda mempengaruhi variabel respon.

ANOVA tiga arah kurang umum dibandingkan ANOVA satu arah (dengan hanya satu faktor) atau ANOVA dua arah (dengan hanya dua faktor), namun masih digunakan di berbagai bidang.

Setiap kali kami melakukan ANOVA tiga arah, kami ingin mengetahui apakah terdapat hubungan yang signifikan secara statistik antara masing-masing faktor dan variabel respons, serta apakah terdapat efek interaksi antar faktor.

Tutorial ini menunjukkan beberapa skenario di mana Anda dapat menggunakan ANOVA tiga arah, serta contoh cara menjalankannya.

Kapan menggunakan ANOVA tiga arah

Berikut beberapa skenario di mana Anda dapat menggunakan ANOVA tiga arah:

Skenario 1: Botani

Seorang ahli botani mungkin ingin menentukan bagaimana (1) paparan sinar matahari, (2) frekuensi penyiraman, dan (3) jenis pupuk mempengaruhi pertumbuhan tanaman.

Dalam skenario ini, ia dapat melakukan ANOVA tiga arah karena terdapat tiga faktor dan satu variabel respon.

Skenario 2: Ritel

Manajer toko ritel mungkin ingin menentukan bagaimana (1) hari dalam seminggu, (2) lokasi toko, dan (3) kampanye iklan mempengaruhi total penjualan.

Dalam skenario ini, ia dapat melakukan ANOVA tiga arah karena terdapat tiga faktor dan satu variabel respon.

Skenario 3: Medis

Seorang dokter mungkin ingin menentukan bagaimana (1) jenis kelamin, (2) pola makan, dan (3) kebiasaan olahraga mempengaruhi berat badan.

Dalam skenario ini, ia dapat melakukan ANOVA tiga arah karena terdapat tiga faktor dan satu variabel respon.

ANOVA tiga arah: contoh

Misalkan seorang peneliti ingin mengetahui apakah program latihan, jenis kelamin, dan pembagian olahraga mempengaruhi tinggi lompatan.

Untuk mengujinya, ia dapat melakukan ANOVA tiga arah dengan faktor-faktor berikut:

• 1. Program pelatihan (program 1 vs program 2)
• 2. Jenis Kelamin (pria atau wanita)
• 3. Divisi olahraga (divisi I vs divisi II)

Satu-satunya variabel respons adalah ketinggian lompatan .

Misalkan dia mengumpulkan data ini pada 40 orang:

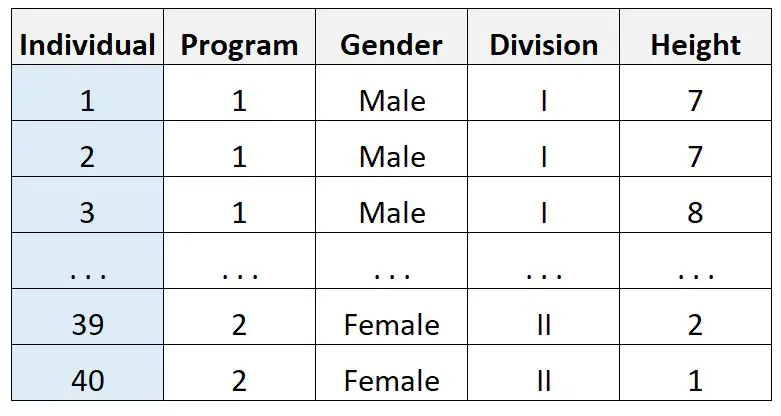
Dia kemudian menggunakan perangkat lunak statistik untuk melakukan ANOVA tiga arah dan menerima hasil berikut:

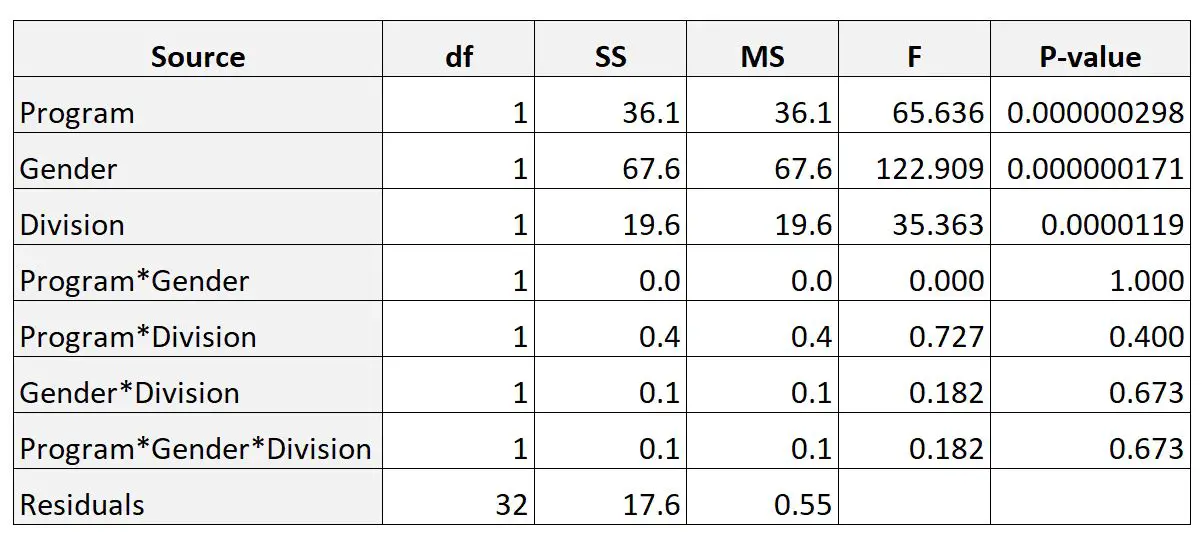
Kolom P-Value menampilkan P-value untuk masing-masing faktor dan interaksi antar faktor.

Dari hasil tersebut, kita dapat melihat bahwa tidak ada interaksi antara ketiga faktor tersebut yang signifikan secara statistik.

Kita juga dapat melihat bahwa ketiga faktor tersebut (Program, Gender dan Pembagian) signifikan secara statistik.

Sebagai kesimpulan, kami dapat mengatakan bahwa program pelatihan, gender, dan pembagian merupakan indikator signifikan peningkatan tinggi lompatan pemain.

Kami juga dapat mengatakan bahwa tidak ada efek interaksi yang signifikan antara ketiga faktor ini.

Catatan : Dalam praktiknya, kami juga akan menghitung rata-rata tinggi lompatan untuk setiap program, jenis kelamin, dan divisi sehingga kami dapat menentukan tingkat setiap faktor yang terkait dengan peningkatan tinggi lompatan.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan ANOVA tiga arah dengan R dan Python:

Cara melakukan ANOVA tiga arah di R
Cara Melakukan ANOVA Tiga Arah dengan Python