Apa artinya jika suatu statistik memiliki ketahanan?

Suatu statistik dikatakan resilient apabila tidak sensitif terhadap nilai-nilai ekstrim.

Berikut adalah dua contoh statistik tangguh:

• median
• Rentang interkuartil

Berikut adalah contoh statistik yang tidak bertahan :

• Rata-rata
• Deviasi standar
• Rapi

Contoh berikut mengilustrasikan perbedaan antara statistik yang tangguh dan tidak resisten.

Contoh: Statistik resisten dan non-resisten

Misalkan kita memiliki kumpulan data berikut:

Kumpulan data: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29

Dengan menggunakan kalkulator atau perangkat lunak statistik, kita dapat menghitung nilai statistik penyimpanan berikut untuk kumpulan data ini:

• Median: 13
• Rentang interkuartil: 13,5

Kami juga dapat menghitung nilai statistik non-resilien berikut untuk kumpulan data ini:

• Rata-rata: 13,54
• Deviasi standar: 8,82
• Kisaran: 27

Sekarang pertimbangkan apakah kumpulan data ini memiliki tambahan pencilan ekstrem:

Kumpulan data: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450

Kita dapat menghitung kembali nilai statistik ketahanan berikut untuk kumpulan data ini:

• Median: 14
• Kisaran interkuartil: 15,75

Kami juga dapat menghitung nilai statistik non-resilien berikut untuk kumpulan data ini:

• Rata-rata: 49,92
• Deviasi standar: 126,27
• Kisaran: 448

Perhatikan seberapa besar perubahan statistik non-resistensi hanya dengan menambahkan nilai ekstrem ke kumpulan data:

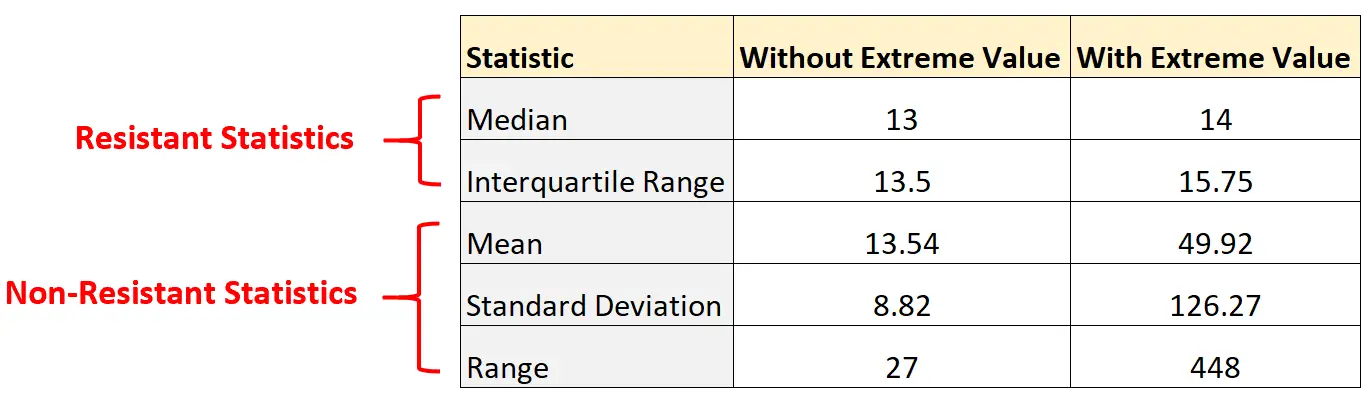
Sebaliknya, statistik para pejuang perlawanan tidak banyak berubah. Rentang median dan interkuartil hanya mengalami sedikit perubahan.

Kapan menggunakan statistik tangguh

Statistik yang paling umum digunakan untuk mengukur pusat dan penyebaran nilai dalam suatu kumpulan data adalah mean dan deviasi standar.

Sayangnya, kedua statistik ini sensitif terhadap nilai ekstrim. Jadi, jika terdapat outlier pada suatu kumpulan data, maka mean dan deviasi standarnya tidak akan menggambarkan sebaran nilai dalam suatu kumpulan data secara akurat.

Sebaliknya, disarankan untuk menggunakan rentang median dan interkuartil untuk mengukur pusat dan penyebaran nilai dalam kumpulan data jika terdapat outlier, karena kedua statistik ini kuat .

Sumber daya tambahan

Bagaimana pengaruh outlier terhadap mean?
Kapan menggunakan mean versus median
Kapan menggunakan rentang interkuartil versus deviasi standar