Empat asumsi regresi linier

Regresi linier adalah metode statistik berguna yang dapat kita gunakan untuk memahami hubungan antara dua variabel, x dan y. Namun, sebelum melakukan regresi linier, pertama-tama kita harus memastikan bahwa empat asumsi terpenuhi:

1. Hubungan linier : Terdapat hubungan linier antara variabel bebas, x, dan variabel terikat, y.

2. Independensi: Residunya bersifat independen. Secara khusus, tidak ada korelasi antara residu yang berurutan dalam data deret waktu.

3. Homoskedastisitas : Residual mempunyai varian yang konstan pada setiap level x.

4. Normalitas: Residual model berdistribusi normal.

Jika satu atau lebih asumsi ini tidak terpenuhi, maka hasil regresi linier kami mungkin tidak dapat diandalkan atau bahkan menyesatkan.

Pada artikel ini kami memberikan penjelasan untuk setiap asumsi, cara menentukan asumsi terpenuhi, dan apa yang harus dilakukan jika asumsi tidak terpenuhi.

Hipotesis 1: Hubungan linier

Penjelasan

Asumsi regresi linier yang pertama adalah terdapat hubungan linier antara variabel bebas x dengan variabel bebas y.

Bagaimana menentukan apakah asumsi ini terpenuhi

Cara paling sederhana untuk mendeteksi apakah asumsi ini terpenuhi adalah dengan membuat plot sebar x versus y. Hal ini memungkinkan Anda melihat secara visual apakah ada hubungan linier antara kedua variabel. Jika titik-titik pada plot tampak terletak sepanjang garis lurus, maka terdapat hubungan linier antara kedua variabel dan asumsi ini terpenuhi.

Misalnya, titik-titik pada grafik di bawah tampak terletak pada garis lurus, yang menunjukkan adanya hubungan linier antara x dan y:

Namun, tampaknya tidak ada hubungan linier antara x dan y pada grafik di bawah ini:

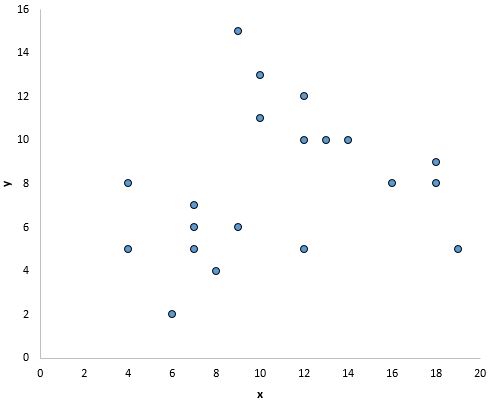
Dan pada grafik ini terlihat terdapat hubungan yang jelas antara x dan y, namun tidak terdapat hubungan linier :

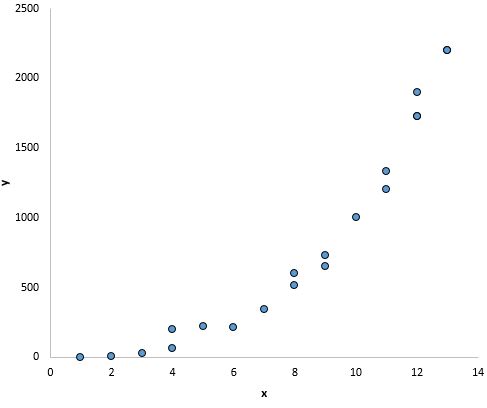
Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Jika Anda membuat plot sebar nilai untuk x dan y dan menemukan bahwa tidak ada hubungan linier antara kedua variabel, Anda memiliki beberapa opsi:

1. Menerapkan transformasi nonlinier pada variabel bebas dan/atau terikat. Contoh umum termasuk mengambil log, akar kuadrat, atau kebalikan dari variabel independen dan/atau dependen.

2. Tambahkan variabel independen lain ke dalam model. Misalnya, jika plot x versus y berbentuk parabola, masuk akal untuk menambahkan X ² sebagai variabel independen tambahan dalam model.

Hipotesis 2: Kemandirian

Penjelasan

Asumsi regresi linier selanjutnya adalah residunya independen. Hal ini sangat relevan ketika bekerja dengan data deret waktu. Idealnya, kita tidak ingin ada tren di antara residu yang berurutan. Misalnya, residu tidak boleh bertambah terus menerus seiring berjalannya waktu.

Bagaimana menentukan apakah asumsi ini terpenuhi

Cara paling sederhana untuk menguji apakah asumsi ini berlaku adalah dengan melihat plot residu deret waktu, yang merupakan plot residu versus waktu. Idealnya, sebagian besar autokorelasi sisa harus berada dalam pita kepercayaan 95% di sekitar nol, yang terletak kira-kira +/- 2 pada akar kuadrat n , dengan n adalah ukuran sampel. Anda juga dapat menguji secara formal apakah asumsi ini terpenuhi menggunakan uji Durbin-Watson .

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Bergantung pada bagaimana asumsi ini dilanggar, Anda memiliki beberapa pilihan:

• Untuk korelasi serial positif, pertimbangkan untuk menambahkan lag variabel dependen dan/atau independen ke dalam model.
• Untuk korelasi serial negatif, pastikan tidak ada variabel yang mengalami over-delayed .
• Untuk korelasi musiman, pertimbangkan untuk menambahkan boneka musiman ke model.

Hipotesis 3: Homoskedastisitas

Penjelasan

Asumsi regresi linier selanjutnya adalah residu memiliki varian konstan pada setiap level x. Hal ini disebut homoskedastisitas . Jika hal ini tidak terjadi, maka residunya mengalami heteroskedastisitas .

Ketika terdapat heteroskedastisitas dalam analisis regresi, hasil analisis menjadi sulit dipercaya. Secara khusus, heteroskedastisitas meningkatkan varians estimasi koefisien regresi, namun model regresi tidak memperhitungkannya. Hal ini membuat model regresi lebih mungkin mengklaim bahwa suatu istilah dalam model tersebut signifikan secara statistik, padahal kenyataannya tidak.

Bagaimana menentukan apakah asumsi ini terpenuhi

Cara termudah untuk mendeteksi heteroskedastisitas adalah dengan membuat plot nilai/sisa yang sesuai .

Setelah Anda memasukkan garis regresi ke kumpulan data, Anda dapat membuat plot sebar yang memperlihatkan nilai-nilai yang dipasang pada model dibandingkan dengan sisa dari nilai-nilai yang dipasang tersebut. Plot sebar di bawah menunjukkan plot khas dari nilai yang dipasang versus residu di mana terdapat heteroskedastisitas.

Perhatikan bagaimana residu semakin menyebar seiring dengan meningkatnya nilai yang dipasang. Bentuk “kerucut” ini merupakan tanda klasik heteroskedastisitas:

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Ada tiga cara umum untuk mengoreksi heteroskedastisitas:

1. Transformasikan variabel terikat. Transformasi yang umum dilakukan adalah dengan mengambil log variabel terikat. Misalnya, jika kita menggunakan ukuran populasi (variabel independen) untuk memprediksi jumlah toko bunga di suatu kota (variabel dependen), kita dapat mencoba menggunakan ukuran populasi untuk memprediksi logaritma jumlah toko bunga di sebuah kota. Penggunaan log variabel dependen, bukan variabel dependen asli, sering kali mengakibatkan hilangnya heteroskedastisitas.

2. Definisikan kembali variabel terikat. Cara umum untuk mendefinisikan ulang variabel terikat adalah dengan menggunakan tarif , bukan nilai mentah. Misalnya, daripada menggunakan ukuran populasi untuk memprediksi jumlah toko bunga di suatu kota, kita dapat menggunakan ukuran populasi untuk memprediksi jumlah toko bunga per kapita. Dalam kebanyakan kasus, hal ini mengurangi variabilitas yang secara alami terjadi dalam populasi yang lebih besar karena kita mengukur jumlah toko bunga per orang, bukan jumlah toko bunga itu sendiri.

3. Gunakan regresi tertimbang. Cara lain untuk mengoreksi heteroskedastisitas adalah dengan menggunakan regresi tertimbang. Jenis regresi ini memberikan bobot pada setiap titik data berdasarkan varians dari nilai yang dipasang. Pada dasarnya, hal ini memberikan bobot rendah pada titik data yang memiliki varian lebih tinggi, sehingga mengurangi kuadrat residunya. Jika bobot yang digunakan sesuai maka masalah heteroskedastisitas dapat dihilangkan.

Hipotesis 4: normalitas

Penjelasan

Asumsi regresi linier selanjutnya adalah residu berdistribusi normal.

Bagaimana menentukan apakah asumsi ini terpenuhi

Ada dua cara umum untuk memeriksa apakah asumsi ini terpenuhi:

1. Verifikasi hipotesis secara visual menggunakan plot QQ .

Plot QQ, kependekan dari plot kuantil-kuantil, adalah jenis plot yang dapat kita gunakan untuk menentukan apakah residu suatu model mengikuti distribusi normal atau tidak. Jika titik-titik pada plot kira-kira membentuk garis lurus diagonal, maka asumsi normalitas terpenuhi.

Plot QQ berikut menunjukkan contoh residu yang kira-kira mengikuti distribusi normal:

Namun, plot QQ di bawah ini menunjukkan contoh kasus di mana residu jelas menyimpang dari garis lurus diagonal, yang menunjukkan bahwa residu tersebut tidak mengikuti distribusi normal:

2. Anda juga dapat memeriksa asumsi normalitas menggunakan uji statistik formal seperti Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre atau D’Agostino-Pearson. Namun, perlu diingat bahwa pengujian ini sensitif terhadap ukuran sampel yang besar – artinya, pengujian ini sering kali menyimpulkan bahwa residu tidak normal jika ukuran sampel Anda besar. Inilah sebabnya mengapa seringkali lebih mudah menggunakan metode grafis seperti plot QQ untuk memverifikasi hipotesis ini.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Jika asumsi normalitas tidak terpenuhi, Anda memiliki beberapa pilihan:

• Pertama, periksa apakah outlier tidak berdampak besar pada distribusi. Jika ada outlier, pastikan itu adalah nilai sebenarnya dan bukan kesalahan entri data.
• Kemudian Anda dapat menerapkan transformasi nonlinier ke variabel independen dan/atau dependen. Contoh umum termasuk mengambil log, akar kuadrat, atau kebalikan dari variabel independen dan/atau dependen.

Bacaan lebih lanjut:

Pengantar Regresi Linier Sederhana
Pengertian Heteroskedastisitas dalam Analisis Regresi
Cara membuat dan menafsirkan plot QQ di R