Hipotesis varians konstan: definisi & contoh

Regresi linier adalah teknik yang kami gunakan untuk mengukur hubungan antara satu atau lebih variabel prediktor dan variabel respons .

Salah satu asumsi utama regresi linier adalah bahwa residu memiliki varian yang konstan di setiap tingkat variabel prediktor.

Jika asumsi ini tidak terverifikasi, maka residu akan mengalami heteroskedastisitas . Jika hal ini terjadi, estimasi koefisien model menjadi tidak dapat diandalkan.

Cara mengevaluasi varians konstan

Cara paling umum untuk menentukan apakah residu model regresi memiliki varian yang konstan adalah dengan membuat plot nilai yang dipasang terhadap residu .

Ini adalah jenis plot yang menampilkan nilai-nilai yang dipasang dari model regresi di sepanjang sumbu x dan sisa dari nilai-nilai tersebut yang dipasang di sepanjang sumbu y.

Jika distribusi residu kira-kira sama pada setiap tingkat nilai yang dipasang, maka asumsi varians konstan terpenuhi.

Sebaliknya, jika sebaran residu bertambah atau berkurang secara sistematis, asumsi ini kemungkinan besar dilanggar.

Catatan : Jenis plot ini hanya dapat dibuat setelah model regresi disesuaikan dengan kumpulan data.

Bagan berikut menunjukkan contoh plot nilai yang dipasang versus residu yang menampilkan varians konstan :

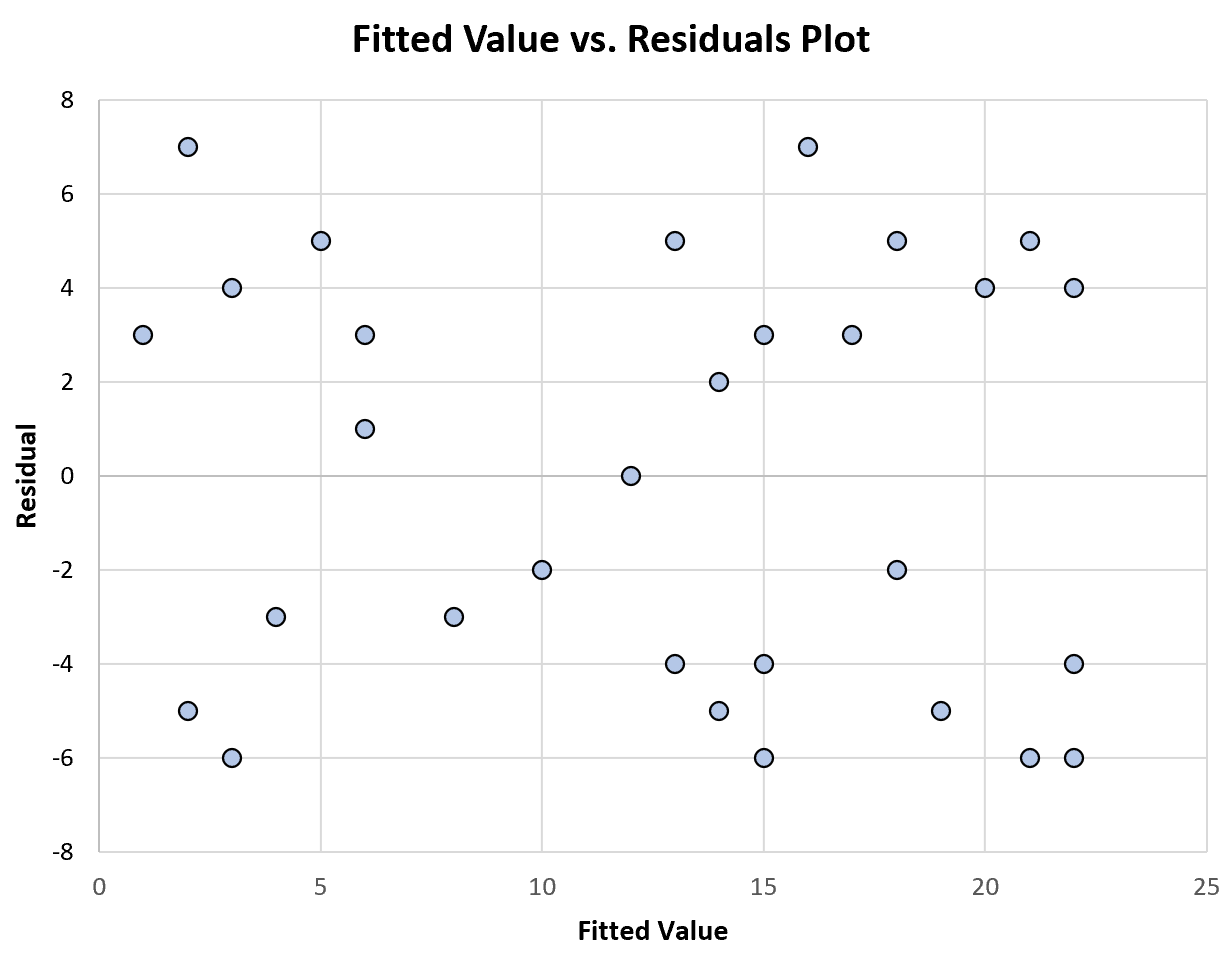
Perhatikan bagaimana residu tersebar secara acak di sekitar nol, tanpa pola tertentu, dengan varians yang kira-kira konstan pada setiap tingkat nilai yang dipasang.

Bagan berikut menunjukkan contoh plot nilai pas versus residu yang menampilkan varians tidak konstan :

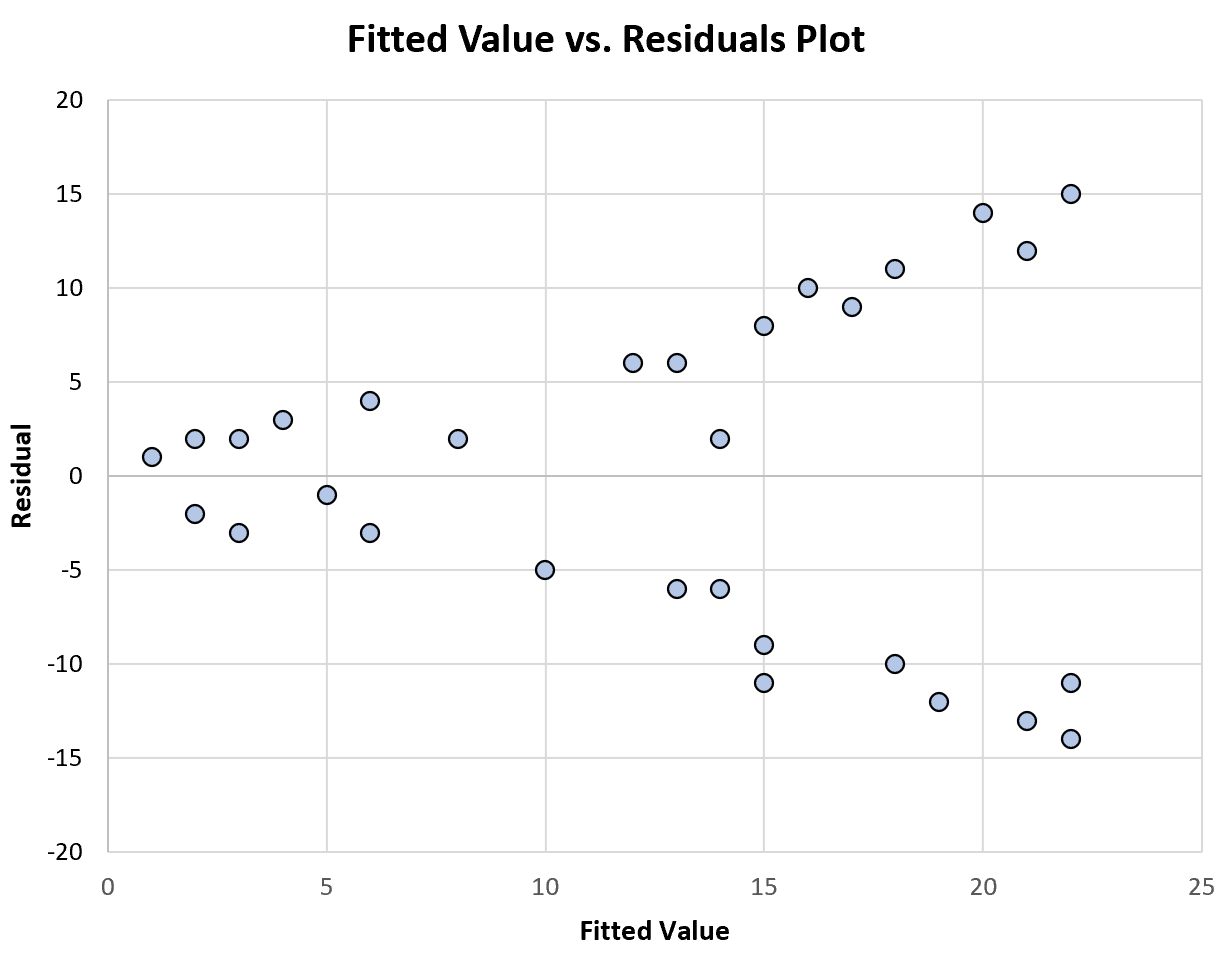
Perhatikan bahwa distribusi residu menjadi lebih besar seiring dengan meningkatnya nilai yang dipasang. Ini adalah tanda khas dari varians yang tidak konstan.

Hal ini menunjukkan bahwa model regresi kita mempunyai variansi yang tidak konstan dalam residu dan oleh karena itu estimasi koefisien model tidak dapat diandalkan.

Cara memperbaiki pelanggaran varians konstan

Jika asumsi varians konstan dilanggar, cara paling umum untuk menyelesaikan masalah ini adalah dengan mentransformasikan variabel respon menggunakan salah satu dari tiga transformasi:

1. Transformasi Log: Transformasikan variabel respon dari y menjadi log(y)

2. Transformasi akar kuadrat: mengubah variabel respon dari y menjadi √y

3. Transformasi akar pangkat tiga: transformasi variabel respon dari y menjadi y ^1/3

Dengan melakukan transformasi ini, masalah variansi non-konstan secara umum akan hilang.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang regresi linier dan analisis residu:

Pengantar Regresi Linier Sederhana
Pengantar Regresi Linier Berganda
Empat asumsi regresi linier
Apa yang dimaksud dengan residu dalam statistik?