Aturan penjumlahan (atau aturan penjumlahan)

Artikel ini menjelaskan apa itu aturan penjumlahan, juga dikenal sebagai aturan penjumlahan, dan kegunaannya dalam probabilitas dan statistik. Selain itu, Anda akan dapat melihat rumus aturan penjumlahan dan menyelesaikan latihan yang menunjukkan cara menggunakannya.

Apa aturan penjumlahan (atau aturan penjumlahan)?

Aturan penjumlahan (atau aturan penjumlahan ) menyatakan bahwa jumlah peluang dua kejadian sama dengan jumlah peluang masing-masing kejadian terjadi secara terpisah dikurangi peluang kedua kejadian terjadi pada waktu yang sama.

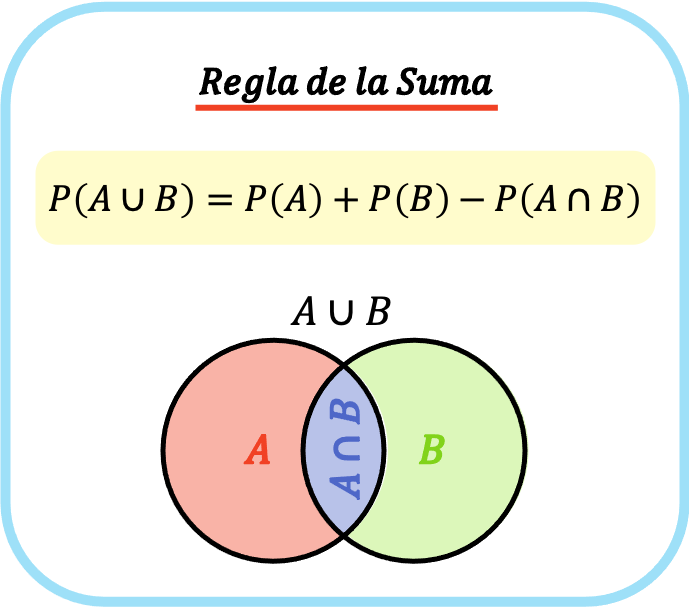
Oleh karena itu, rumus aturan penjumlahan adalah P(A⋃B)=P(A)+P(B)−P(A⋂B).

Jadi, untuk menjumlahkan dua probabilitas, kita tidak bisa begitu saja menjumlahkan masing-masing probabilitas, karena kita juga harus mengurangkan suku yang mewakili probabilitas gabungan dari dua kejadian. Namun, dalam beberapa kasus, hanya dengan menjumlahkan probabilitas setiap kejadian kita dapat memperoleh hasil penjumlahan probabilitas yang benar. Di bawah ini kita akan melihat apa saja kasus-kasus tersebut.

Singkatnya, aturan penjumlahan digunakan untuk menghitung peluang terjadinya suatu peristiwa, yaitu peluang terjadinya paling sedikit satu dari dua kemungkinan peristiwa.

Rumus aturan penjumlahan

Aturan penjumlahan mengatakan bahwa untuk menghitung peluang terjadinya peristiwa A atau peristiwa B, kita harus menjumlahkan peluang terjadinya peristiwa A ditambah peluang terjadinya peristiwa B dan mengurangi peluang terjadinya kedua peristiwa tersebut pada waktu yang sama. .

Oleh karena itu , rumus aturan penjumlahan (atau aturan penjumlahan) adalah sebagai berikut:

Emas:

• 

  adalah peluang kejadian A atau kejadian B.

• 

  adalah peluang terjadinya kejadian A.

• 

  adalah peluang terjadinya kejadian B.

• 

  adalah peluang gabungan terjadinya kejadian A dan kejadian B.

Oleh karena itu, untuk menggunakan aturan penjumlahan, Anda perlu mengetahui cara menghitung probabilitas gabungan dari dua kejadian. Anda dapat melihat cara melakukannya di tautan berikut:

Contoh aturan penjumlahan untuk acara eksklusif

Untuk menyelesaikan pemahaman konsepnya, mari kita lihat contoh bagaimana menerapkan aturan penjumlahan.

• Kami memasukkan 10 bola biru, 6 bola oranye, dan 4 bola hijau ke dalam sebuah kotak. Berapa peluang terambilnya bola biru atau oranye?

Latihan ini meminta kita untuk menentukan probabilitas suatu peristiwa atau peristiwa lainnya akan terjadi. Oleh karena itu, untuk menyelesaikan soal tersebut kita perlu menggunakan rumus aturan penjumlahan:

Jadi, pertama-tama kita hitung peluang setiap kejadian terjadi secara terpisah menggunakan aturan Laplace :

Namun dalam hal ini kedua peristiwa tersebut tidak dapat terjadi pada waktu yang bersamaan, karena keduanya merupakan dua peristiwa yang saling lepas . Jadi jika kita menggambar bola biru kita tidak bisa lagi menggambar bola oranye, begitu pula sebaliknya.

Oleh karena itu, probabilitas gabungan dari kedua kejadian adalah nol dan karenanya rumus aturan penjumlahan disederhanakan:

Maka perhitungan peluang terambilnya bola biru atau bola jingga adalah sebagai berikut:

Singkatnya, peluang terambilnya bola biru atau oranye dari kotak adalah 80%.

Contoh penambahan aturan untuk acara non-eksklusif

Setelah melihat contoh konkrit aturan penjumlahan ketika kejadian bersifat eksklusif, sekarang kita akan melihat bagaimana hukum ini digunakan ketika kejadian bersifat non-eksklusif.

• Jika kita melempar sebuah uang logam sebanyak dua kali, berapakah peluang munculnya gambar paling sedikit dalam satu kali pelemparan?

Dalam hal ini, kejadian-kejadian tersebut tidak saling eksklusif, karena kita bisa mendapatkan “kepala” pada lemparan pertama dan “ekor” pada lemparan kedua. Oleh karena itu, rumus aturan penjumlahan tidak disederhanakan dan menjadi sebagai berikut:

Jadi, pertama-tama kita perlu menghitung probabilitas munculnya “kepala” pada pelemparan koin dengan menerapkan aturan Laplace:

Selain itu, kedua kejadian tersebut saling bebas, sehingga kita dapat menghitung probabilitas gabungan dari kedua kejadian tersebut menggunakan aturan hasil kali :

Terakhir, untuk mencari peluang jatuhnya kepala pada setidaknya satu dari dua pelemparan, cukup substitusikan nilainya ke dalam rumus aturan penjumlahan dan lakukan perhitungan:

Kesimpulannya, peluang munculnya gambar paling sedikit satu kali dengan pelemparan sebuah koin sebanyak dua kali adalah 75%.