Perbandingan skor z dari distribusi yang berbeda

Skor-z memberi tahu Anda berapa banyak standar deviasi suatu nilai data individual yang turun dari rata-ratanya. Ini dihitung sebagai berikut:

skor-z = (x – μ) / σ

Emas:

• x: nilai data individu
• μ: rata-rata populasi
• σ: deviasi standar populasi

Skor-z untuk suatu nilai individu dapat diartikan sebagai berikut:

• Skor-z positif: nilai individu di atas rata-rata.
• Skor-z negatif: nilai individu lebih rendah dari rata-rata.
• Skor z 0: nilai individu sama dengan rata-rata.

Skor Z sangat berguna ketika kita ingin membandingkan posisi relatif dua titik data dari dua distribusi berbeda. Untuk mengilustrasikannya, perhatikan contoh berikut.

Contoh: Membandingkan Skor Z

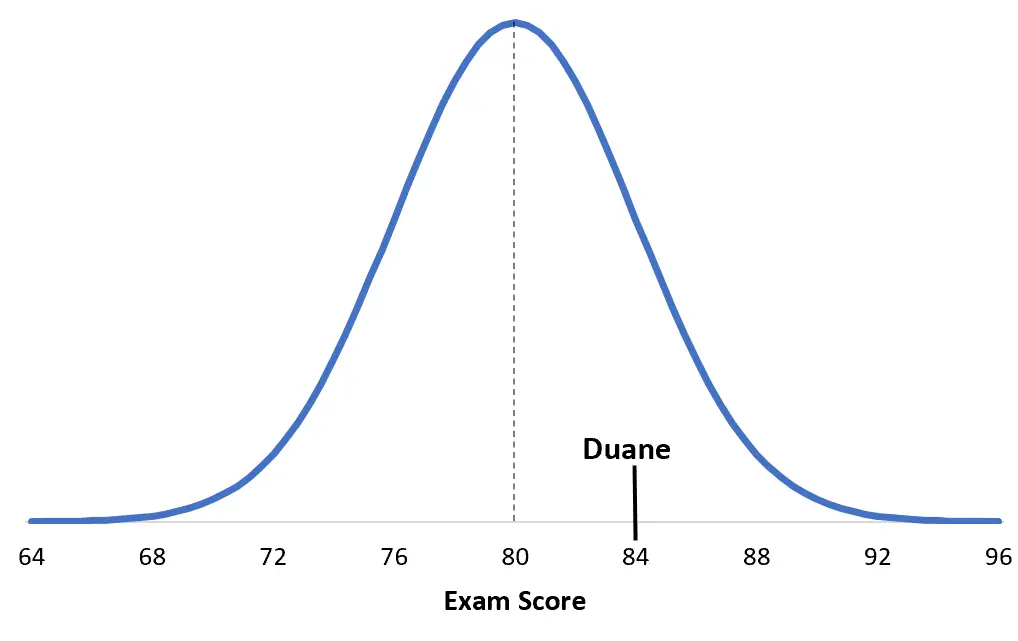
Nilai ujian perguruan tinggi tertentu berdistribusi normal dengan mean μ = 80 dan simpangan baku σ = 4. Duane mendapat nilai 84 pada ujian ini.

Nilai ujian perguruan tinggi lain berdistribusi normal dengan mean μ = 85 dan deviasi standar σ = 8. Debbie mendapat nilai 90 pada ujian itu.

Dibandingkan dengan distribusi nilai ujian mereka sendiri, siapa yang memperoleh hasil terbaik dalam ujian mereka?

Untuk menjawab pertanyaan ini, kita dapat menghitung z-score dari nilai ujian setiap orang:

Skor z Duane = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

Skor-z Debbie = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625

Debbie Meski mendapat nilai lebih tinggi, sebenarnya nilai Duane lebih tinggi dibandingkan distribusi ujian khususnya.

Untuk memahami hal ini, ada baiknya memvisualisasikan situasinya. Berikut skor Duane dibandingkan dengan rincian ujian khususnya:

Dan inilah nilai Debbie dari rincian ujiannya:

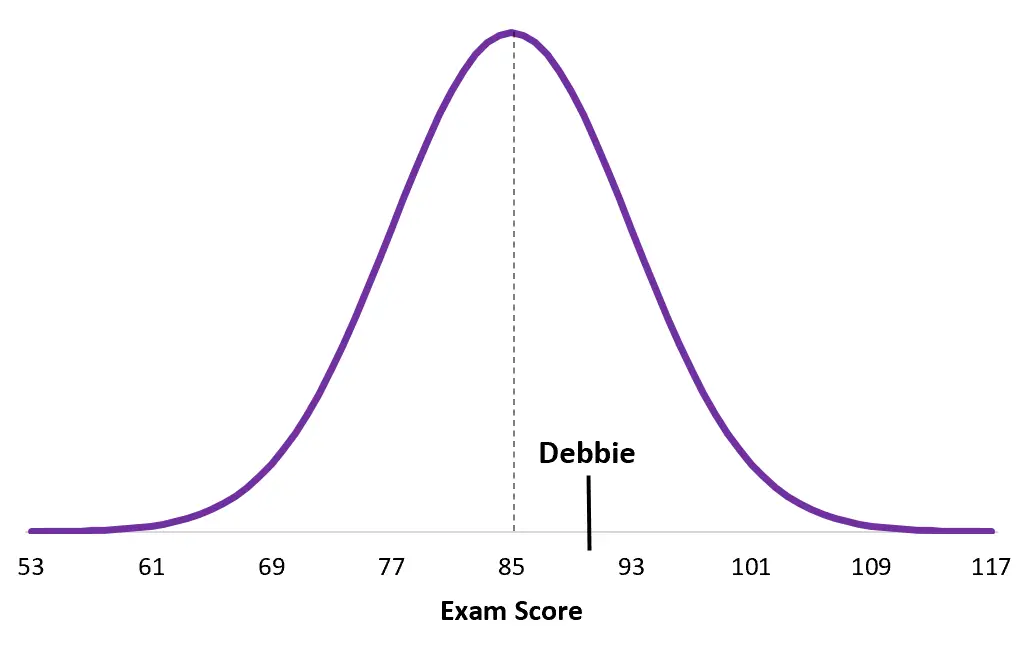
Perhatikan seberapa dekat skor Debbie dengan rata-rata populasinya dibandingkan dengan skor Duane. Walaupun secara keseluruhan dia mempunyai nilai yang lebih tinggi, nilai z-nya lebih rendah karena nilai rata-rata pada ujian khususnya lebih tinggi.

Contoh ini mengilustrasikan mengapa skor-z sangat berguna untuk membandingkan nilai data dari distribusi yang berbeda: skor-z memperhitungkan mean dan deviasi standar dari distribusi, yang memungkinkan kita membandingkan nilai data dari distribusi yang berbeda dan melihat mana yang lebih tinggi dibandingkan dengan distribusi mereka sendiri.

Sumber daya tambahan

Kalkulator skor Z
Bandingkan Kalkulator Skor Z