Batas kendali

Oleh Benjamin anderson Agustus 2, 2023 Manajemen mutu 0 Komentar

Artikel ini menjelaskan apa itu batas kendali dan apa saja batas kendali yang berbeda dari diagram kendali. Anda juga akan melihat bagaimana batas kendali dihitung serta contoh kerja di mana batas kendali suatu proses ditentukan.

Apa yang dimaksud dengan batas kendali?

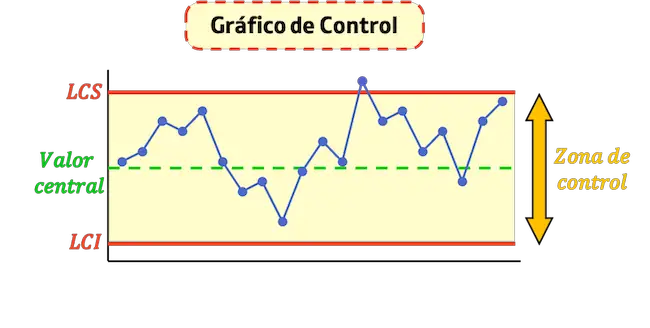
Batas kendali adalah garis horizontal pada peta kendali yang digunakan untuk menentukan apakah suatu proses dikendalikan atau tidak.

Peta kendali memiliki dua batas kendali: batas kendali atas dan bawah, yang masing-masing membatasi area kendali di atas dan di bawah.

Jadi, batas kendali adalah nilai yang digunakan untuk menunjukkan wilayah kendali suatu proses. Jika pengukuran yang diperoleh dari suatu proses berada dalam batas kendali, berarti proses tersebut terkendali. Jika tidak, mesin atau proses harus diperiksa karena kemungkinan besar terjadi penyimpangan.

Jenis batas kendali

Batas kendalinya adalah:

Batas Kendali Atas (LCS) : ini adalah garis yang menunjukkan nilai maksimum yang diterima dalam proses.
Batas Kendali Bawah (LCI) : Ini adalah garis yang menunjukkan nilai minimum yang diterima dalam proses.
Garis kendali pusat : Ini adalah garis yang mewakili nilai rata-rata grafik. Semakin dekat titik-titik tersebut ke garis ini, semakin stabil prosesnya.

Cara Menghitung Batas Kendali

Saat ini, batas kendali suatu proses umumnya dihitung oleh perangkat lunak komputer yang memungkinkan proses tersebut dikendalikan. Namun, penting juga bagi Anda untuk mengetahui cara menghitungnya, karena Anda mungkin perlu menemukannya secara manual.

Menghitung batas kendali suatu diagram kendali bergantung pada jenis diagram yang ingin Anda buat, karena nilainya akan berubah bergantung pada apakah diagram kendali tersebut untuk mean atau untuk rentang.

Peta kendali rata-rata adalah grafik di mana evolusi rata-rata suatu proses dievaluasi. Jadi, rata-rata sekumpulan nilai dihitung dengan menggunakan rumus berikut:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Emas:

$x_i$

adalah ukuran nomor i.
$n$

adalah jumlah pengukuran yang dilakukan.

Kami akan menetapkan nilai sentral dari peta kendali untuk mean sebagai

$\overline{\overline{X}}$

, yang merupakan rata-rata sampel dan dihitung dengan ekspresi berikut:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Emas:

$\overline{X}_j$

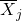
adalah rata-rata sampel j.
$m$

adalah jumlah sampel yang diambil.

➤ Lihat: Perhitungan mean aritmatika

Sebaliknya, nilai sentral dari peta kendali luasan adalah rata-rata luasan seluruh sampel yang diambil:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Emas:

$R_j$

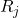
adalah kisaran sampel j.
$m$

adalah jumlah sampel yang diambil.

➤ Lihat: Perhitungan rentang statistik

Dengan demikian, rumus untuk menghitung batas kendali suatu peta kendali adalah sebagai berikut:

kartu kendali

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

Kartu kendali R

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Dimana nilai parameter A ₂ , D ₃ dan D ₄ terdapat pada tabel berikut :

Ukuran (tidak.)	Pukul ₂	hari ke ₃	_J4
2	1.880	0,000	3.267
3	1.023	0,000	2.575
4	0,729	0,000	2.282
5	0,577	0,000	2.115
6	0,483	0,000	2004
7	0,419	0,076	1.924
8	0,373	0,136	1.864
9	0,337	0,184	1.816
sepuluh	0,308	0,223	1.777

Contoh penghitungan batas kendali

Suatu perusahaan industri ingin mengontrol pengukuran diameter silinder untuk melihat apakah proses produksinya terkendali. Untuk melakukan ini, ambil sampel 5 silinder setiap 15 menit dan ukur diameternya. Tabel berikut menunjukkan pencatatan pengukuran.

Untuk mencari batas kendali, pertama-tama kita harus mengambil mean aritmatika dan rentang setiap rangkaian pengukuran:

Sekarang mari kita hitung rata-rata rata-rata dan rentang, yang masing-masing akan menjadi nilai sentral dari diagram kendali untuk rata-rata dan rentang:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

Dalam hal ini setiap sampel terdiri dari 5 pengukuran, maka koefisien rumus batas kendalinya adalah sebagai berikut:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Kami menghitung batas kendali atas dan bawah dari grafik kendali rata-rata dan diperpanjang:

Batas Kendali Bagan Kendali

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Batas kendali dari Kartu kendali R

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

Oleh karena itu, kartu kendali latihannya adalah sebagai berikut:

Pada diagram kendali pertama kita dapat melihat dua nilai yang lebih kecil dari batas kendali bawah. Selain itu, pada peta kendali kedua juga terdapat nilai yang berada di atas batas kendali atas. Oleh karena itu, prosesnya tidak terkontrol.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Apa yang dimaksud dengan batas kendali?

Jenis batas kendali

Cara Menghitung Batas Kendali

Contoh penghitungan batas kendali

Tentang Penulis

Benjamin anderson

Tambahkan komentar