Distribusi bernoulli dan distribusi binomial: apa bedanya?

Suatu variabel acak mengikuti distribusi Bernoulli jika hanya mempunyai dua kemungkinan hasil: 0 atau 1.

Misalnya kita melempar sebuah mata uang satu kali. Biarkan hal . Artinya peluang mendaratnya ekor adalah 1- p .

Jadi, kita bisa menulis:

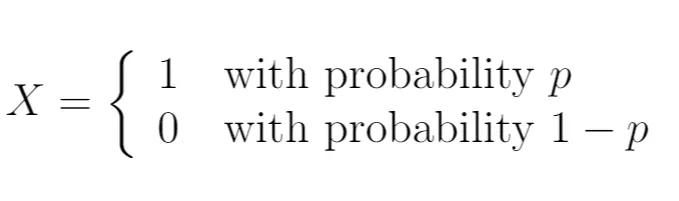
Dalam hal ini, variabel acak X mengikuti distribusi Bernoulli. Ini hanya dapat mengambil dua nilai yang mungkin.

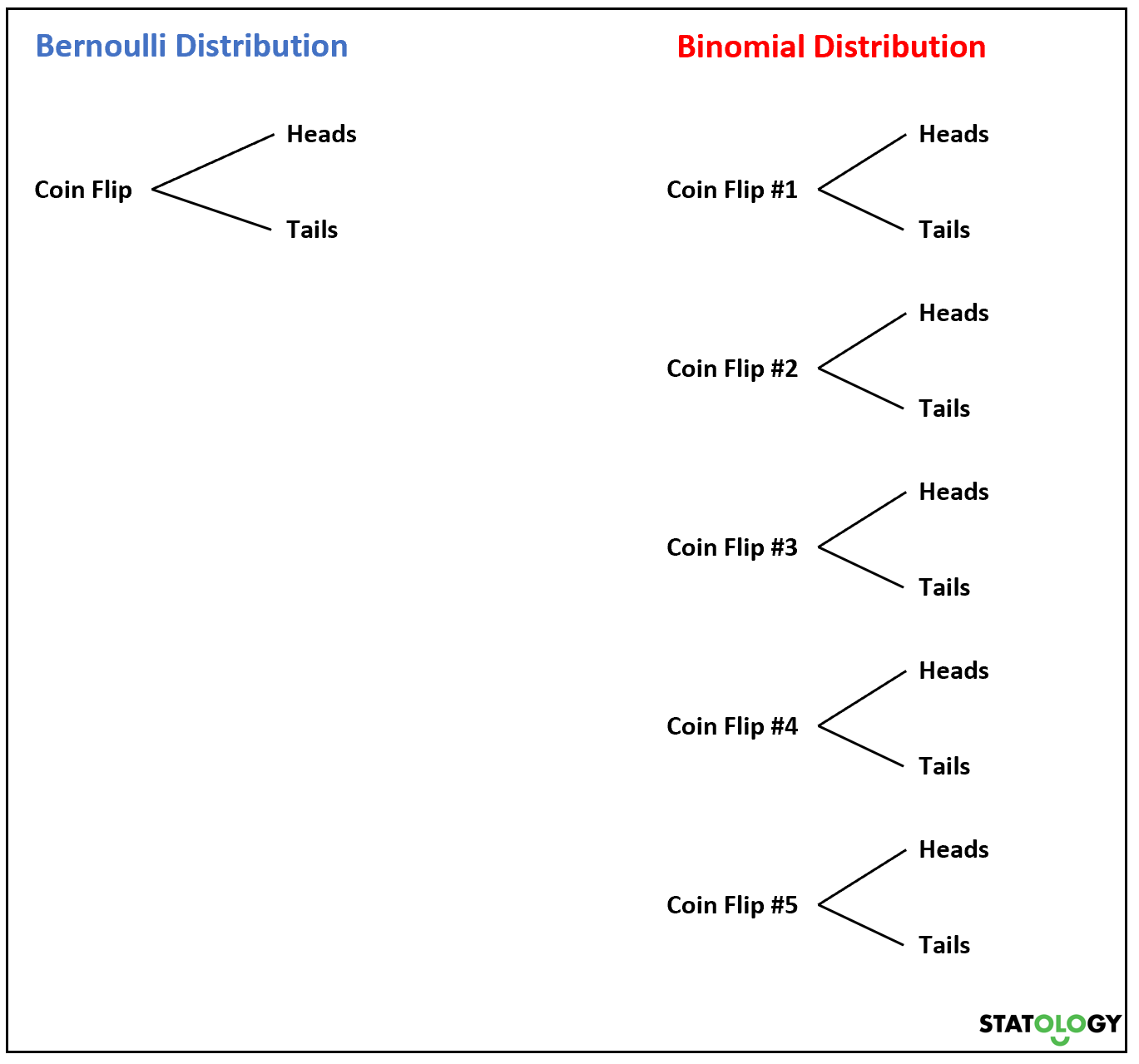
Sekarang, jika kita melempar koin beberapa kali, jumlah variabel acak Bernoulli akan mengikuti distribusi binomial.

Misalnya, kita melempar sebuah koin sebanyak 5 kali dan ingin mengetahui peluang munculnya gambar sebanyak k kali. Sepertinya variabel acak

Jika suatu variabel acak X mengikuti distribusi binomial, maka peluang keberhasilan X = k dapat dicari dengan rumus berikut:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Emas:

• n: jumlah percobaan
• k: jumlah keberhasilan
• p: probabilitas keberhasilan pada percobaan tertentu
• _n C _k : banyaknya cara untuk memperoleh k keberhasilan dalam n percobaan

Misalnya kita melempar sebuah koin sebanyak 3 kali. Kita dapat menggunakan rumus di atas untuk menentukan peluang munculnya 0 gambar dalam 3 kali lemparan berikut:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

Jika n = 1 percobaan maka distribusi binomial ekuivalen dengan distribusi Bernoulli.

Catatan penting

Berikut beberapa catatan penting mengenai distribusi Bernoulli dan Binomial:

1. Variabel acak yang mengikuti distribusi Bernoulli hanya dapat mengambil dua kemungkinan nilai, sedangkan variabel acak yang mengikuti distribusi binomial dapat mengambil beberapa nilai.

Misalnya, dalam satu kali pelemparan koin, kita akan mendapat 0 atau 1 kepala. Namun, dalam rangkaian 5 kali seri kita bisa mendapatkan 0, 1, 2, 3, 4 atau 5 kepala.

2. Agar variabel acak mengikuti distribusi binomial, probabilitas “berhasil” dalam setiap percobaan Bernoulli harus sama dan independen.

Misalnya, jika kita mendefinisikan “sukses” sebagai pendaratan di kepala, maka peluang sukses pada setiap pelemparan adalah 0,5 dan setiap pelemparan bersifat independen – hasil pelemparan tidak mempengaruhi hasil pelemparan lainnya.

Sumber daya tambahan

Pengantar Eksperimen Binomial
Pengenalan distribusi binomial
Memahami bentuk distribusi binomial