Binomial negatif vs poisson: cara memilih model regresi

Regresi binomial negatif dan regresi Poisson adalah dua jenis model regresi yang sebaiknya digunakan jika variabel respons diwakili oleh hasil penghitungan diskrit.

Berikut beberapa contoh variabel respon yang merepresentasikan hasil penghitungan diskrit:

• Banyaknya mahasiswa yang lulus pada suatu program tertentu
• Banyaknya kecelakaan lalu lintas pada suatu persimpangan tertentu
• Jumlah peserta yang menyelesaikan maraton
• Jumlah pengembalian pada bulan tertentu di toko ritel

Jika variansnya kira-kira sama dengan mean, maka model regresi Poisson umumnya cocok untuk kumpulan data.

Namun, jika variansnya jauh lebih besar daripada mean, model regresi binomial negatif umumnya mampu menyesuaikan data dengan lebih baik.

Ada dua teknik yang dapat kita gunakan untuk menentukan apakah regresi Poisson atau regresi binomial negatif lebih tepat untuk kumpulan data tertentu:

1. Plot sisa

Kita dapat membuat plot dari residu terstandar terhadap nilai prediksi dari model regresi.

Jika mayoritas residu terstandar antara -2 dan 2, model regresi Poisson mungkin tepat.

Namun, jika banyak residu berada di luar kisaran ini, model regresi binomial negatif kemungkinan besar akan lebih cocok.

2. Uji rasio kemungkinan

Kita dapat memasukkan model regresi Poisson dan model regresi binomial negatif ke kumpulan data yang sama dan kemudian melakukan uji rasio kemungkinan.

Jika nilai p dari pengujian tersebut berada di bawah tingkat signifikansi tertentu (misalnya 0,05), maka kita dapat menyimpulkan bahwa model regresi binomial negatif memberikan kesesuaian yang jauh lebih baik.

Contoh berikut menunjukkan cara menggunakan kedua teknik ini di R untuk menentukan apakah lebih baik menggunakan model regresi Poisson atau regresi binomial negatif untuk kumpulan data tertentu.

Contoh: regresi binomial negatif vs regresi Poisson

Misalkan kita ingin mengetahui berapa banyak beasiswa yang diterima pemain bisbol sekolah menengah atas di suatu daerah berdasarkan divisi sekolahnya (“A”, “B” atau “C”) dan nilai sekolahnya. ujian masuk universitas (diukur dari 0 hingga 100). ).

Gunakan langkah-langkah berikut untuk menentukan apakah model regresi binomial negatif atau model regresi Poisson lebih cocok dengan data.

Langkah 1: Buat datanya

Kode berikut membuat kumpulan data yang akan kita kerjakan, yang mencakup data 1.000 pemain bisbol:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

Langkah 2: Sesuaikan model regresi Poisson dan model regresi binomial negatif

Kode berikut menunjukkan cara menyesuaikan model regresi Poisson dan model regresi binomial negatif ke dalam data:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

Langkah 3: Buat Plot Sisa

Kode berikut menunjukkan cara membuat plot sisa untuk kedua model.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

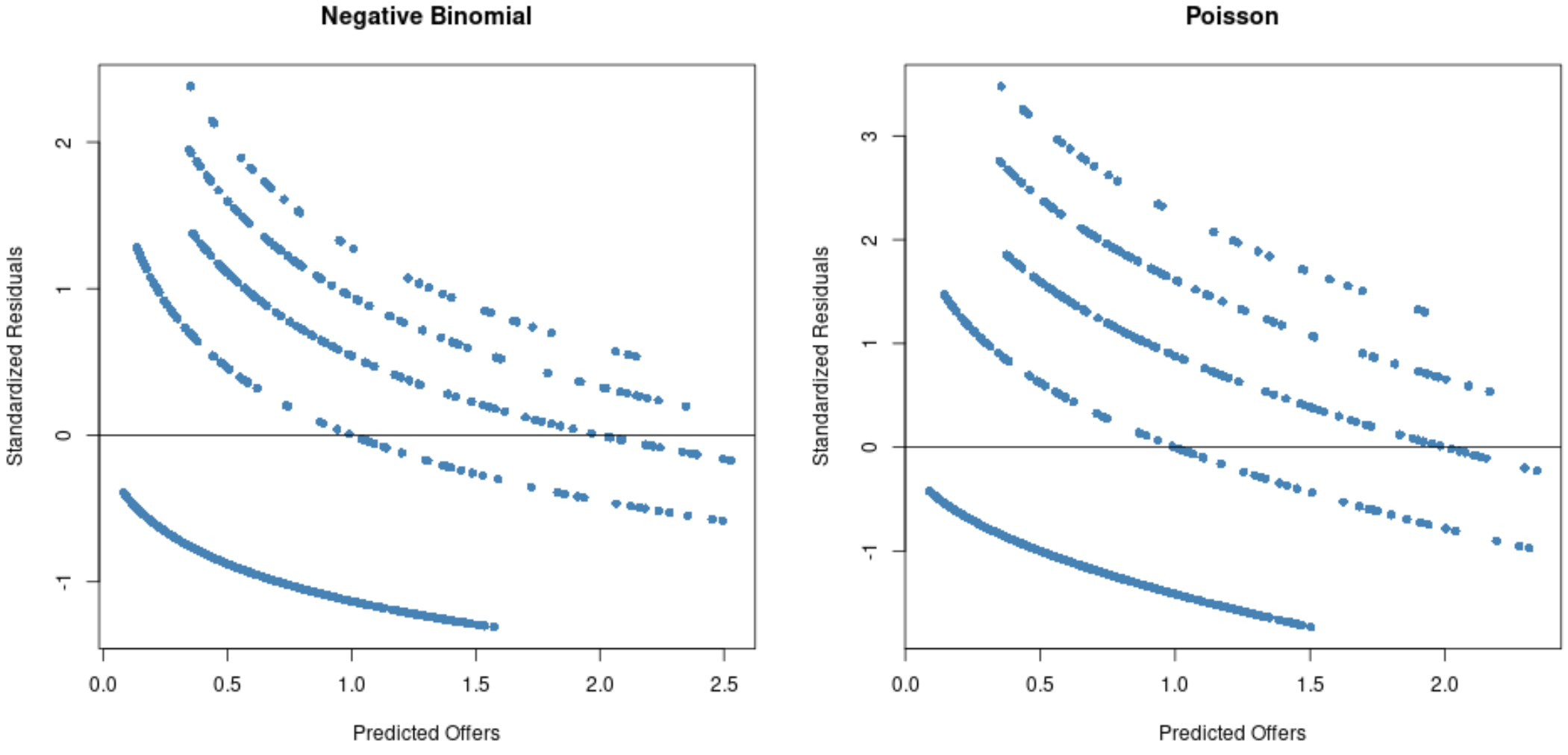
Dari grafik, kita dapat melihat bahwa residu lebih tersebar untuk model regresi Poisson (perhatikan bahwa beberapa residu melampaui 3) dibandingkan dengan model regresi binomial negatif.

Ini merupakan tanda bahwa model regresi binomial negatif mungkin lebih tepat karena residu model ini lebih kecil.

Langkah 4: Lakukan uji rasio kemungkinan

Terakhir, kita dapat melakukan uji rasio kemungkinan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik dalam kesesuaian kedua model regresi:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

Nilai p dari tes tersebut ternyata adalah 3,508072e-29 , yang secara signifikan kurang dari 0,05.

Dengan demikian, kita dapat menyimpulkan bahwa model regresi binomial negatif memberikan kesesuaian yang jauh lebih baik terhadap data dibandingkan dengan model regresi Poisson.

Sumber daya tambahan

Pengenalan distribusi binomial negatif
Pengenalan distribusi Poisson