Bisakah kurtosis menjadi negatif?

Dalam statistik, kurtosis digunakan untuk menggambarkan bentuk distribusi probabilitas.

Secara khusus, ini memberi tahu kita seberapa baik nilai data dikelompokkan di bagian ekor atau di bagian atas distribusi.

Kurtosis suatu distribusi bisa negatif, nol, atau positif.

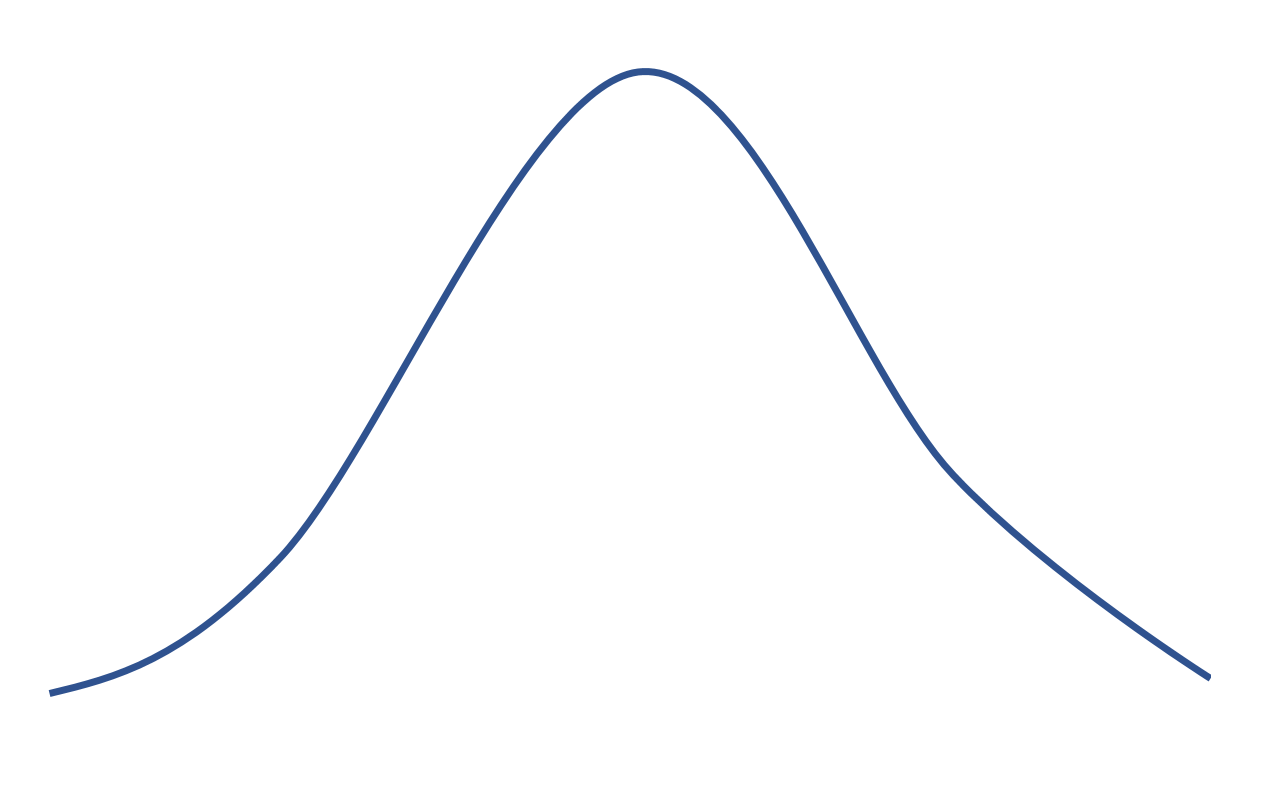
Nol Kurtosis

Jika suatu distribusi mempunyai kurtosis 0, maka distribusi tersebut sama dengan distribusi normal yang berbentuk lonceng sebagai berikut:

Kurtosis positif

Jika suatu distribusi mempunyai kurtosis positif maka dikatakan leptokurtik , artinya mempunyai puncak yang lebih tajam dan ekor yang lebih berat dibandingkan dengan distribusi normal.

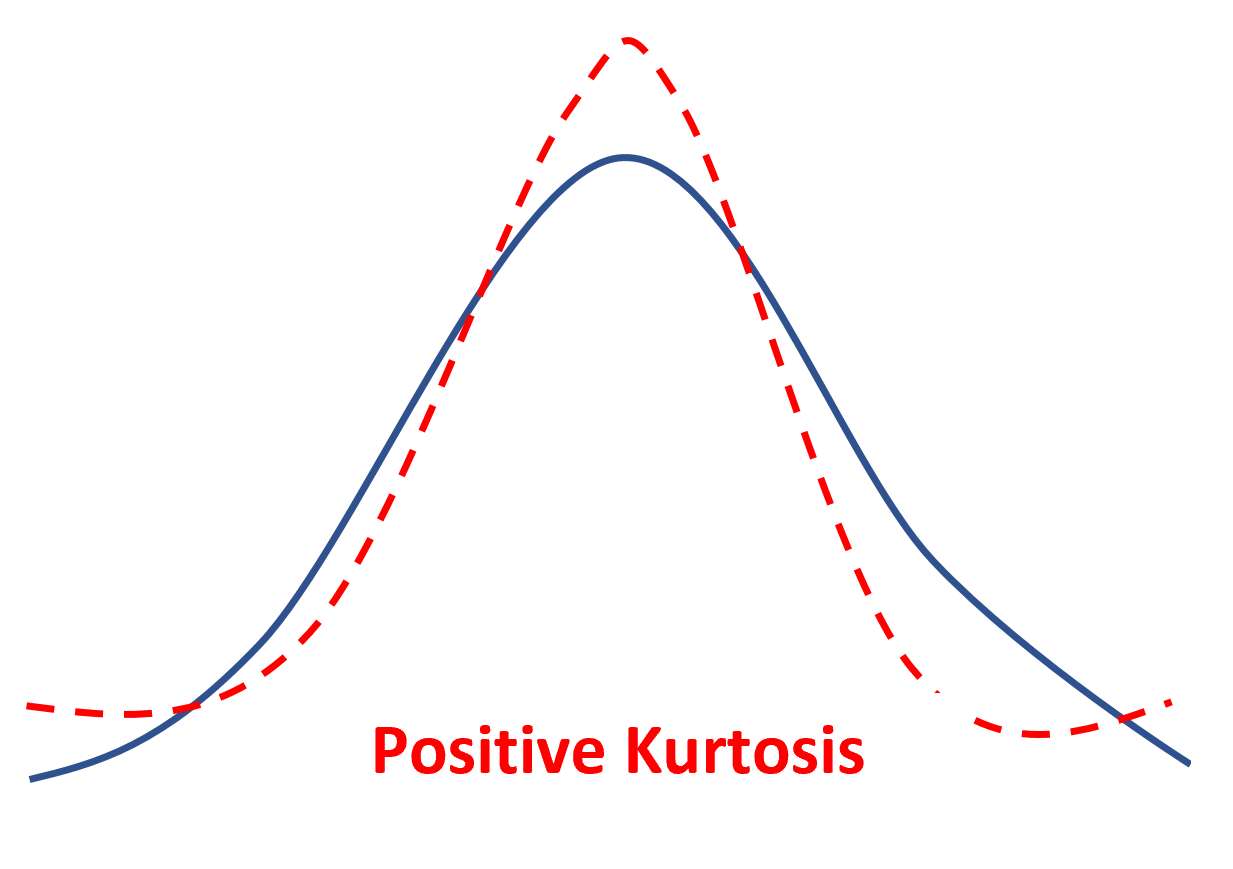
Ini berarti bahwa lebih sedikit nilai data yang terletak di dekat mean dan lebih banyak nilai data yang terletak di bagian ekor.

Distribusi yang paling terkenal memiliki kurtosis positif adalah distribusi t yang mempunyai puncak lebih tajam dan ekor lebih berat dibandingkan distribusi normal.

Kurtosis negatif

Jika suatu distribusi mempunyai kurtosis negatif maka dikatakan platikurtik , artinya mempunyai puncak yang lebih datar dan ekor yang lebih tipis dibandingkan dengan distribusi normal.

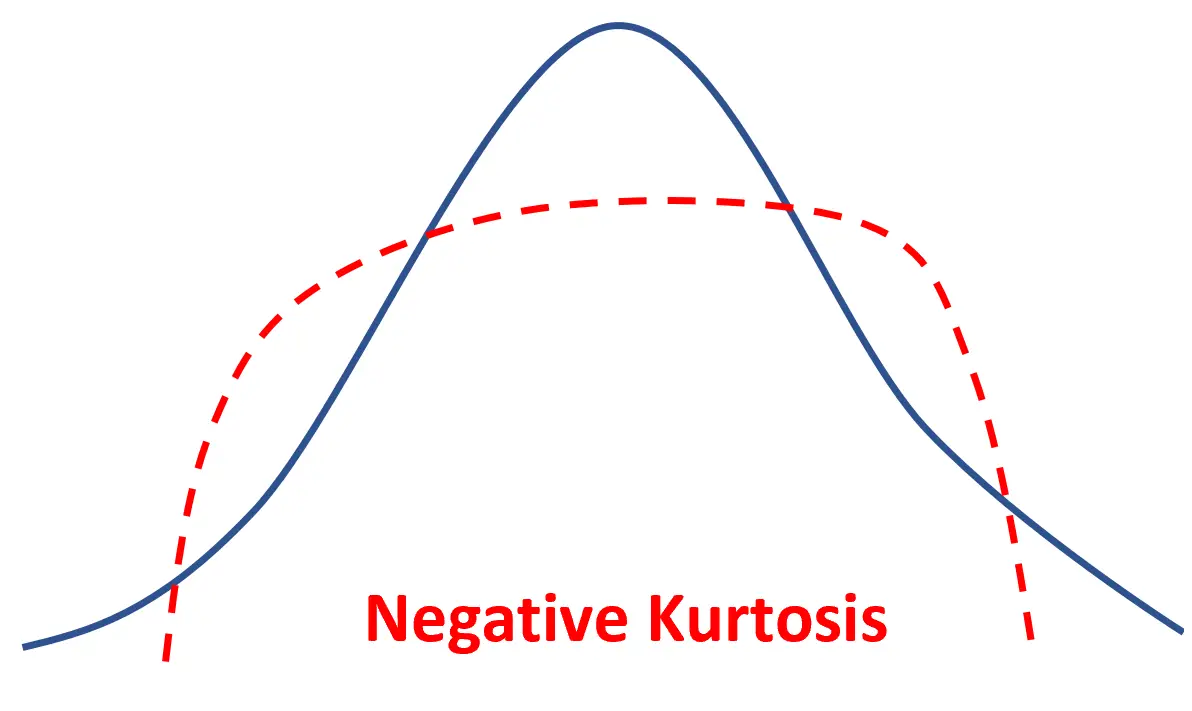
Artinya, lebih banyak nilai data yang terletak di dekat mean dan lebih sedikit nilai data yang terletak di bagian ekor.

Contoh ekstrim dari distribusi yang menunjukkan kurtosis negatif adalah distribusi seragam , yang tidak memiliki puncak dan merupakan distribusi datar seluruhnya.

Kapan menggunakan sanjungan dalam praktik

Dalam praktiknya, kita sering mengukur kurtosis suatu distribusi dalam fase analisis eksplorasi ketika kita sekadar mencoba untuk lebih memahami data.

Jadi jika kita melihat kurtosisnya positif, kita tahu bahwa kita bekerja dengan distribusi yang memiliki lebih sedikit nilai data yang terletak di dekat pusat dan lebih banyak nilai data yang didistribusikan di sepanjang bagian ekor.

Sebaliknya, jika kita melihat kurtosisnya negatif, kita tahu bahwa kita bekerja dengan distribusi yang memiliki lebih banyak nilai data yang terletak di dekat pusat dan lebih sedikit nilai data di bagian ekor.

Sumber daya tambahan

Untuk menemukan skewness dan kurtosis suatu distribusi tertentu, Anda dapat memasukkan nilai data mentah ke dalam kalkulator skewness dan kurtosis ini , yang akan memberi tahu Anda skewness dan kurtosis distribusi tersebut.

Salah satu uji statistik paling populer yang digunakan untuk menentukan apakah suatu distribusi tertentu menunjukkan skewness dan kurtosis yang sesuai dengan distribusi normal adalah uji Jarque Bera .

Khan Academy juga memiliki serangkaian video bagus yang menjelaskan cara mengklasifikasikan bentuk distribusi.