Cara melakukan tes mann-whitney u di excel
Uji Mann-Whitney U (terkadang disebut uji jumlah peringkat Wilcoxon) digunakan untuk membandingkan perbedaan antara dua sampel ketika distribusi sampel tidak terdistribusi normal dan ukuran sampel kecil (n <30).
Ini dianggap setara nonparametrik dari uji t dua sampel .
Tutorial ini menjelaskan cara melakukan tes Mann-Whitney U di Excel.
Contoh: Tes Mann-Whitney U di Excel
Peneliti ingin mengetahui apakah perlakuan bahan bakar menyebabkan perubahan rata-rata mpg mobil. Untuk mengujinya, mereka melakukan percobaan di mana mereka mengukur mpg dari 12 mobil dengan perawatan bahan bakar dan 12 mobil tanpa perawatan.
Karena ukuran sampelnya kecil dan mereka menduga distribusi sampel tidak terdistribusi normal, mereka memutuskan untuk melakukan uji Mann-Whitney U untuk menentukan apakah ada perbedaan mpg yang signifikan secara statistik antara kedua kelompok.
Selesaikan langkah-langkah berikut untuk melakukan tes Mann-Whitney U di Excel.
Langkah 1: Masukkan datanya.
Masukkan data sebagai berikut:
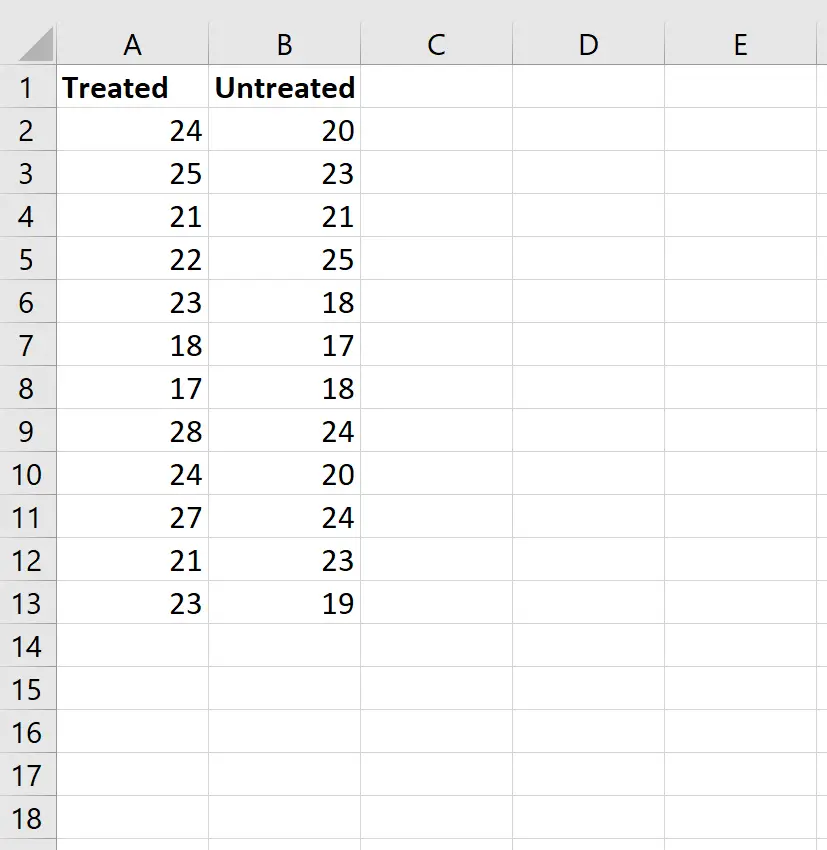
Langkah 2: Hitung peringkat kedua grup.
Selanjutnya kita akan menghitung rangking masing-masing grup. Gambar berikut menunjukkan rumus yang digunakan untuk menghitung peringkat nilai pertama dalam grup Diproses:
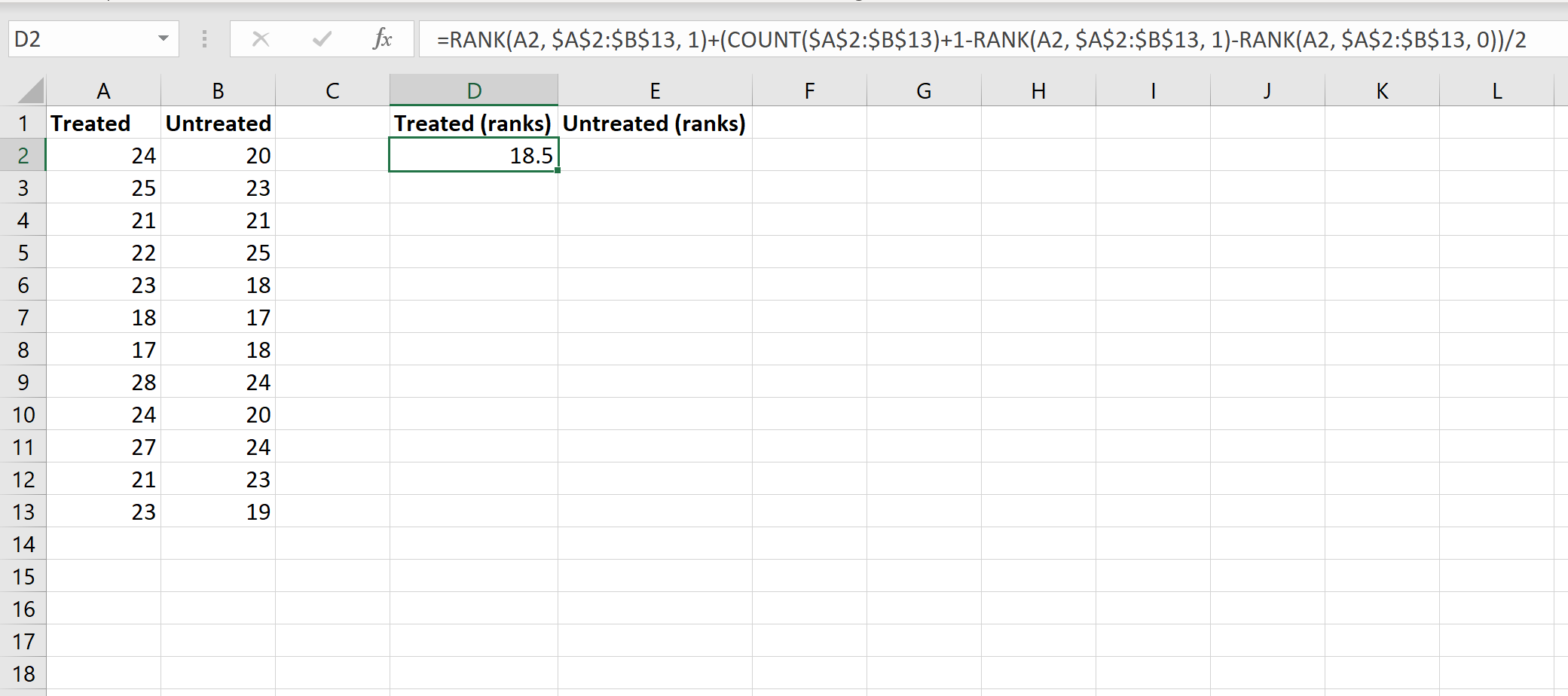
Walaupun rumus ini cukup rumit, namun Anda hanya perlu memasukkannya satu kali saja. Kemudian Anda cukup menyeret rumus ke semua sel lain untuk mengisi baris:
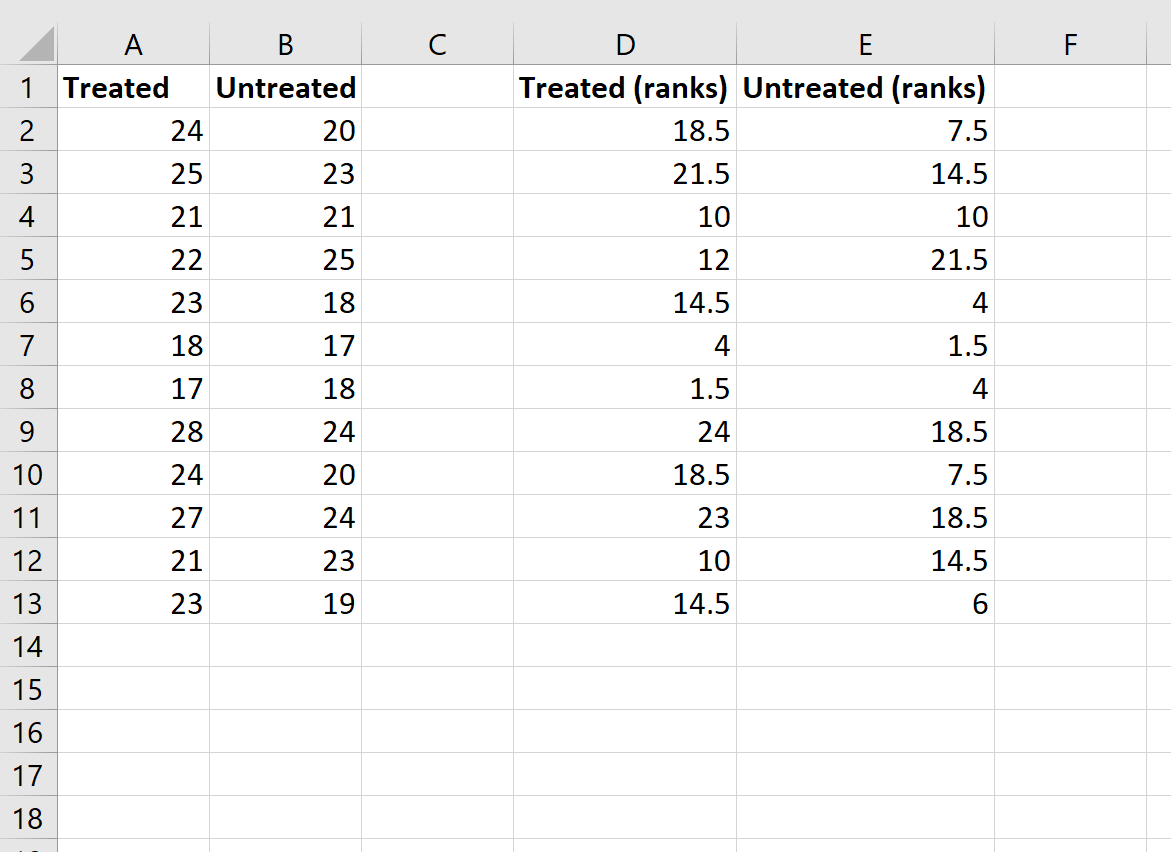
Langkah 3: Hitung nilai yang diperlukan untuk statistik uji.
Selanjutnya, kita akan menggunakan rumus berikut untuk menghitung jumlah peringkat setiap kelompok, ukuran sampel setiap kelompok, statistik uji U setiap kelompok, dan statistik uji U keseluruhan:
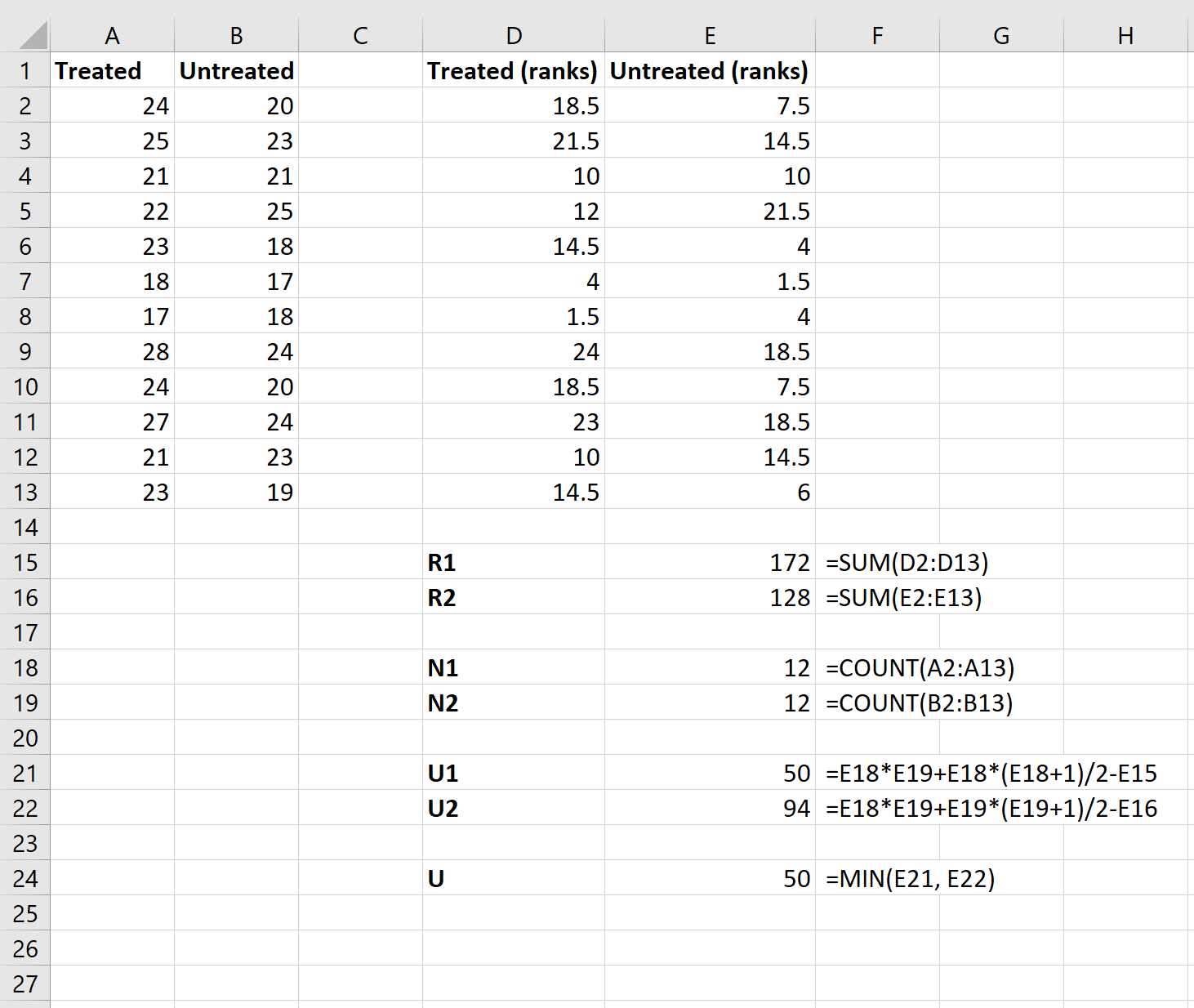
Langkah 4: Hitung statistik uji-z dan nilai p yang sesuai.
Terakhir, kita akan menggunakan rumus berikut untuk menghitung statistik uji-z dan nilai p yang sesuai untuk menentukan apakah kita harus menolak hipotesis nol atau tidak:
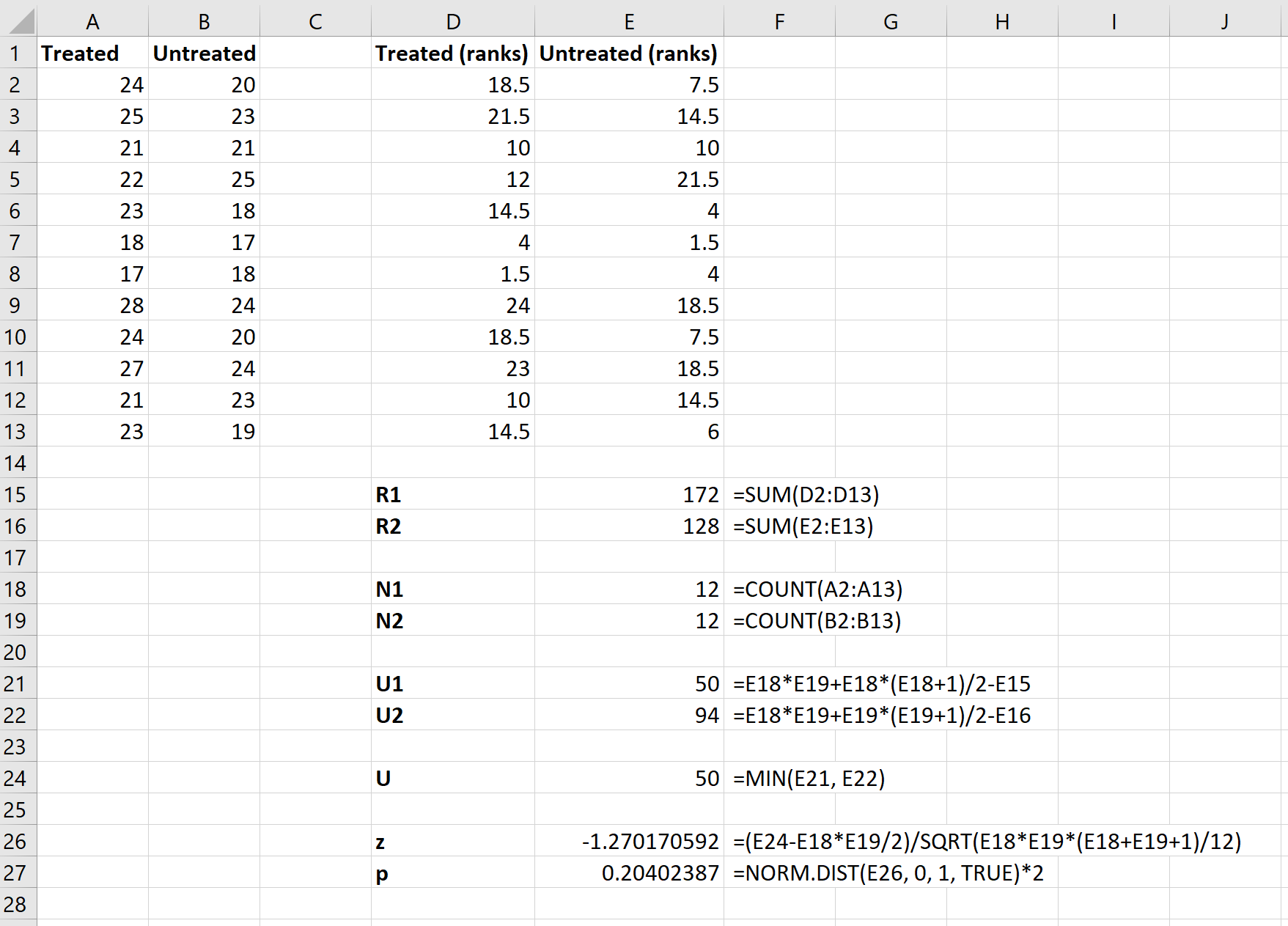
Hipotesis nol dari pengujian tersebut menyatakan bahwa kedua kelompok memiliki rata-rata mpg yang sama. Karena nilai p uji ( 0,20402387 ) tidak kurang dari tingkat signifikansi kami sebesar 0,05, kami gagal menolak hipotesis nol.
Kami tidak memiliki cukup bukti untuk mengatakan bahwa rata-rata mpg sebenarnya berbeda antara kedua kelompok.