Cara membaca matriks korelasi

Dalam statistik, kita sering kali berusaha memahami hubungan antara dua variabel.

Misalnya, kita mungkin ingin memahami hubungan antara jumlah jam belajar siswa dan nilai ujian yang mereka terima.

Salah satu cara untuk mengukur hubungan ini adalah dengan menggunakan koefisien korelasi Pearson , yang merupakan ukuran hubungan linier antara dua variabel . Ini memiliki nilai antara -1 dan 1 di mana:

• -1 menunjukkan korelasi linier negatif sempurna antara dua variabel
• 0 menunjukkan tidak ada korelasi linier antara dua variabel
• Angka 1 menunjukkan korelasi linier positif sempurna antara dua variabel

Semakin jauh koefisien korelasi dari nol maka semakin kuat hubungan kedua variabel tersebut.

Terkait: Apa yang dianggap sebagai korelasi “kuat”?

Namun dalam beberapa kasus, kami ingin memahami korelasi antara beberapa pasangan variabel. Dalam kasus ini, kita dapat membuat matriks korelasi , yaitu tabel persegi yang menunjukkan koefisien korelasi antara beberapa variabel.

Contoh Matriks Korelasi

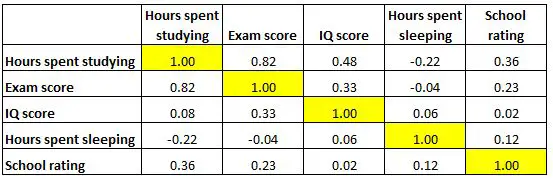
Matriks korelasi di bawah ini menyajikan koefisien korelasi antara beberapa variabel terkait pendidikan:

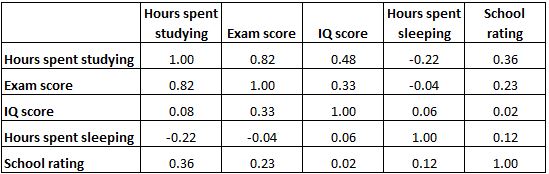
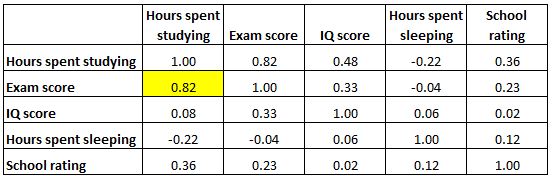
Setiap sel dalam tabel menunjukkan korelasi antara dua variabel tertentu. Misalnya, sel yang disorot di bawah menunjukkan bahwa korelasi antara “jam yang dihabiskan untuk belajar” dan “nilai ujian” adalah 0,82 , yang menunjukkan bahwa keduanya berkorelasi sangat positif. Lebih banyak jam yang dihabiskan untuk belajar berkaitan erat dengan nilai ujian yang lebih tinggi.

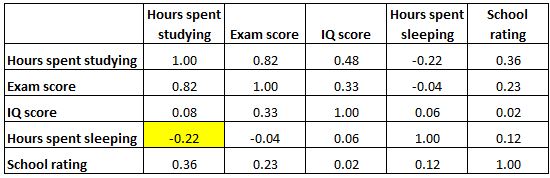
Dan sel yang disorot di bawah ini menunjukkan bahwa korelasi antara “jam yang dihabiskan untuk belajar” dan “jam yang dihabiskan untuk tidur” adalah -0,22 , yang menunjukkan bahwa keduanya berkorelasi negatif lemah. Semakin banyak jam yang dihabiskan untuk belajar berhubungan dengan semakin sedikitnya jam yang dihabiskan untuk tidur.

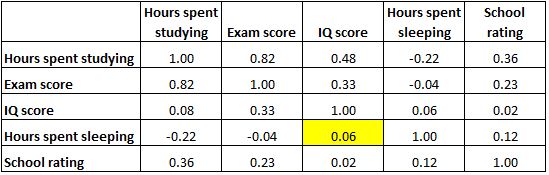
Dan sel yang disorot di bawah ini menunjukkan bahwa korelasi antara “jam yang dihabiskan untuk tidur” dan “skor IQ” adalah 0,06 , yang menunjukkan bahwa keduanya pada dasarnya tidak berkorelasi. Hanya ada sedikit hubungan antara jumlah jam tidur seorang siswa dan nilai IQ mereka.

Perhatikan juga bahwa koefisien korelasi sepanjang diagonal tabel semuanya sama dengan 1 karena setiap variabel berkorelasi sempurna dengan variabelnya sendiri. Sel-sel ini tidak berguna untuk interpretasi.

Variasi matriks korelasi

Perhatikan bahwa matriks korelasi simetris sempurna. Misalnya, sel kanan atas memperlihatkan nilai yang sama persis dengan sel kiri bawah:

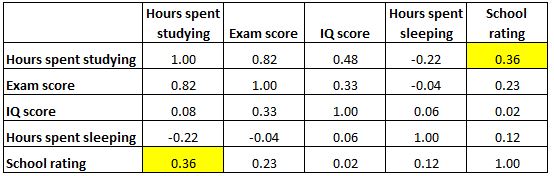
Memang benar, kedua sel tersebut mengukur korelasi antara “jam yang dihabiskan untuk belajar” dan “nilai sekolah”.

Karena matriks korelasi bersifat simetris, setengah dari koefisien korelasi yang ditampilkan dalam matriks adalah mubazir dan tidak diperlukan. Jadi, terkadang hanya setengah dari matriks korelasi yang akan ditampilkan:

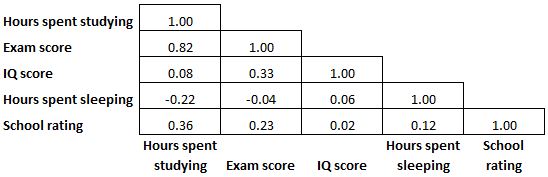
Dan terkadang matriks korelasi akan diwarnai seperti peta panas agar koefisien korelasinya lebih mudah dibaca:

Kapan menggunakan matriks korelasi

Dalam praktiknya, matriks korelasi biasanya digunakan karena tiga alasan:

1. Matriks korelasi dengan mudah merangkum sekumpulan data.

Matriks korelasi adalah cara sederhana untuk meringkas korelasi antara semua variabel dalam suatu kumpulan data. Misalnya, kita memiliki kumpulan data berikut yang berisi informasi berikut untuk 1.000 siswa:

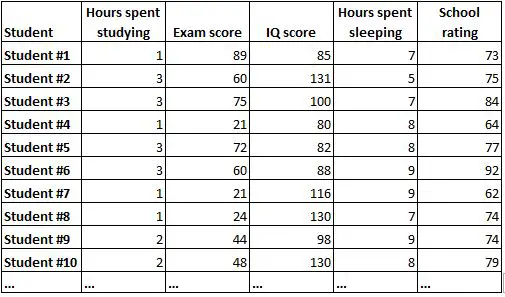
Akan sangat sulit untuk memahami hubungan setiap variabel hanya dengan melihat data mentahnya. Untungnya, matriks korelasi dapat membantu kita dengan cepat memahami korelasi antara setiap pasangan variabel.

2. Matriks korelasi berfungsi sebagai diagnosis regresi.

Salah satu asumsi utama regresi linier berganda adalah tidak ada variabel independen dalam model yang berkorelasi kuat dengan variabel lain dalam model.

Ketika dua variabel independen berkorelasi tinggi, maka akan timbul masalah yang disebut multikolinearitas dan menyulitkan interpretasi hasil regresi.

Salah satu cara paling sederhana untuk menemukan potensi masalah multikolinearitas adalah dengan melihat matriks korelasi dan memeriksa secara visual apakah ada variabel yang berkorelasi tinggi satu sama lain.

3. Matriks korelasi dapat digunakan sebagai masukan untuk analisis lainnya.

Matriks korelasi digunakan sebagai masukan untuk analisis kompleks lainnya seperti analisis faktor eksplorasi dan model persamaan struktural.

Sumber daya tambahan

Tutorial berikut menjelaskan cara membuat matriks korelasi menggunakan berbagai software statistik:

Cara Membuat Matriks Korelasi di Excel
Cara Membuat Matriks Korelasi di SPSS
Cara membuat matriks korelasi di Stata
Cara Membuat Matriks Korelasi dengan Python