Cara membaca tabel distribusi binomial

Tabel distribusi binomial   adalah tabel yang menunjukkan probabilitas yang terkait dengan distribusi binomial . Untuk menggunakan tabel distribusi binomial, Anda hanya memerlukan tiga nilai:

• n: jumlah percobaan
• r: jumlah “keberhasilan” selama n upaya
• p: probabilitas keberhasilan suatu percobaan tertentu

Dengan menggunakan ketiga angka ini, Anda dapat menggunakan tabel distribusi binomial untuk mencari peluang mendapatkan r keberhasilan yang tepat selama n percobaan ketika peluang keberhasilan pada setiap percobaan adalah p .

Contoh berikut menggambarkan cara membaca tabel distribusi binomial.

Contoh 1

Pertanyaan: Jessica melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 6 kali lemparan bebas, berapa peluang dia berhasil melakukan tepat 4 lemparan bebas?

Untuk menjawab pertanyaan ini, kita dapat mencari nilai dalam tabel distribusi binomial yang sesuai dengan n = 6, r = 4, dan p = 0,60:

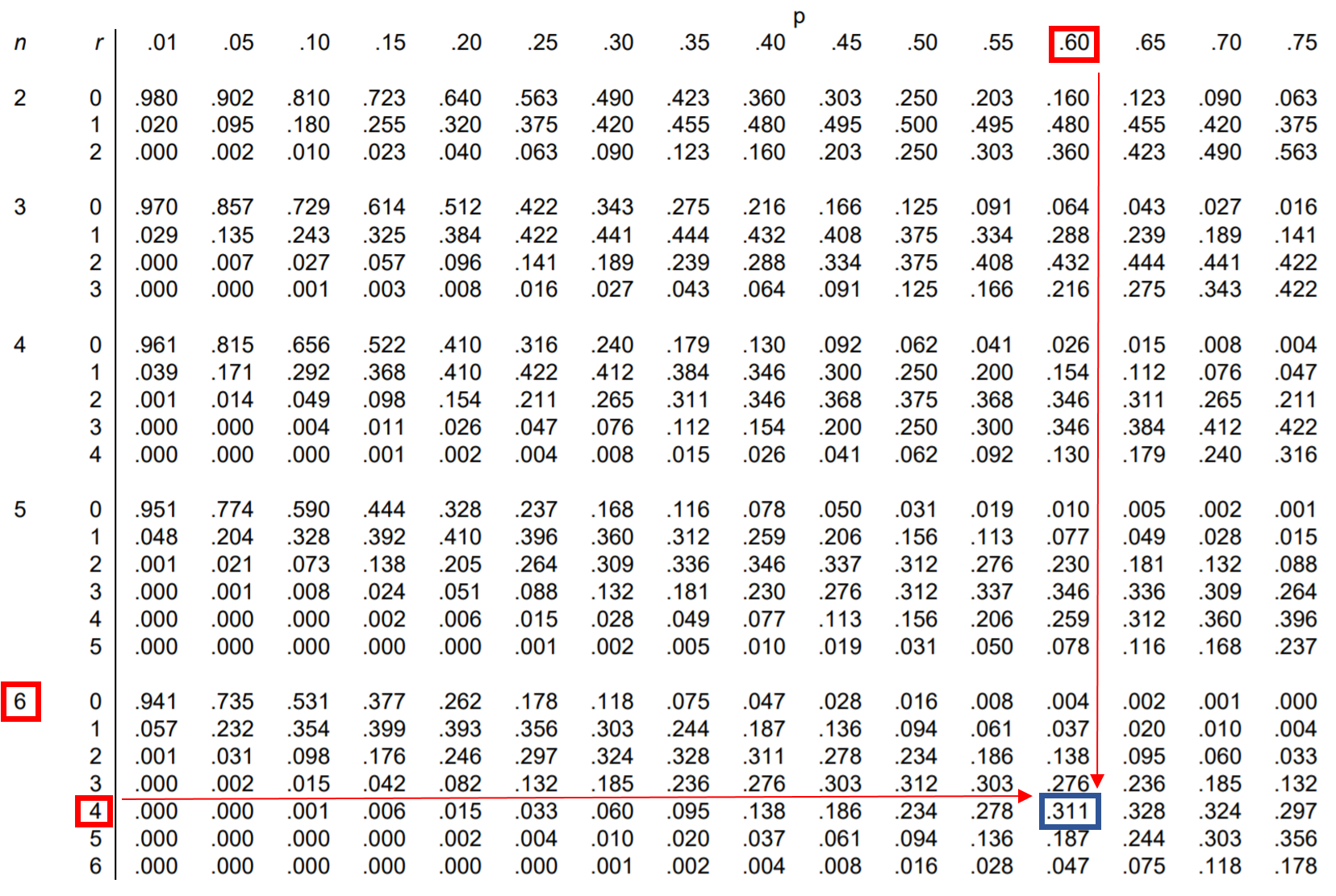
Peluang Jessica melakukan tepat 4 dari 6 lemparan bebas adalah 0,311 .

Contoh 2

Pertanyaan: Jessica melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 6 kali lemparan bebas, berapa peluang dia melakukan kurang dari 4 lemparan bebas?

Untuk mencari probabilitas ini, Anda sebenarnya harus menambahkan probabilitas berikut:

P(hasilnya kurang dari 4) = P(hasilnya 0) + P(hasilnya 1) + P(hasilnya 2) + P(hasilnya 3)

Jadi, kita dapat mencari masing-masing dari empat probabilitas ini dalam tabel distribusi binomial dan menjumlahkannya:

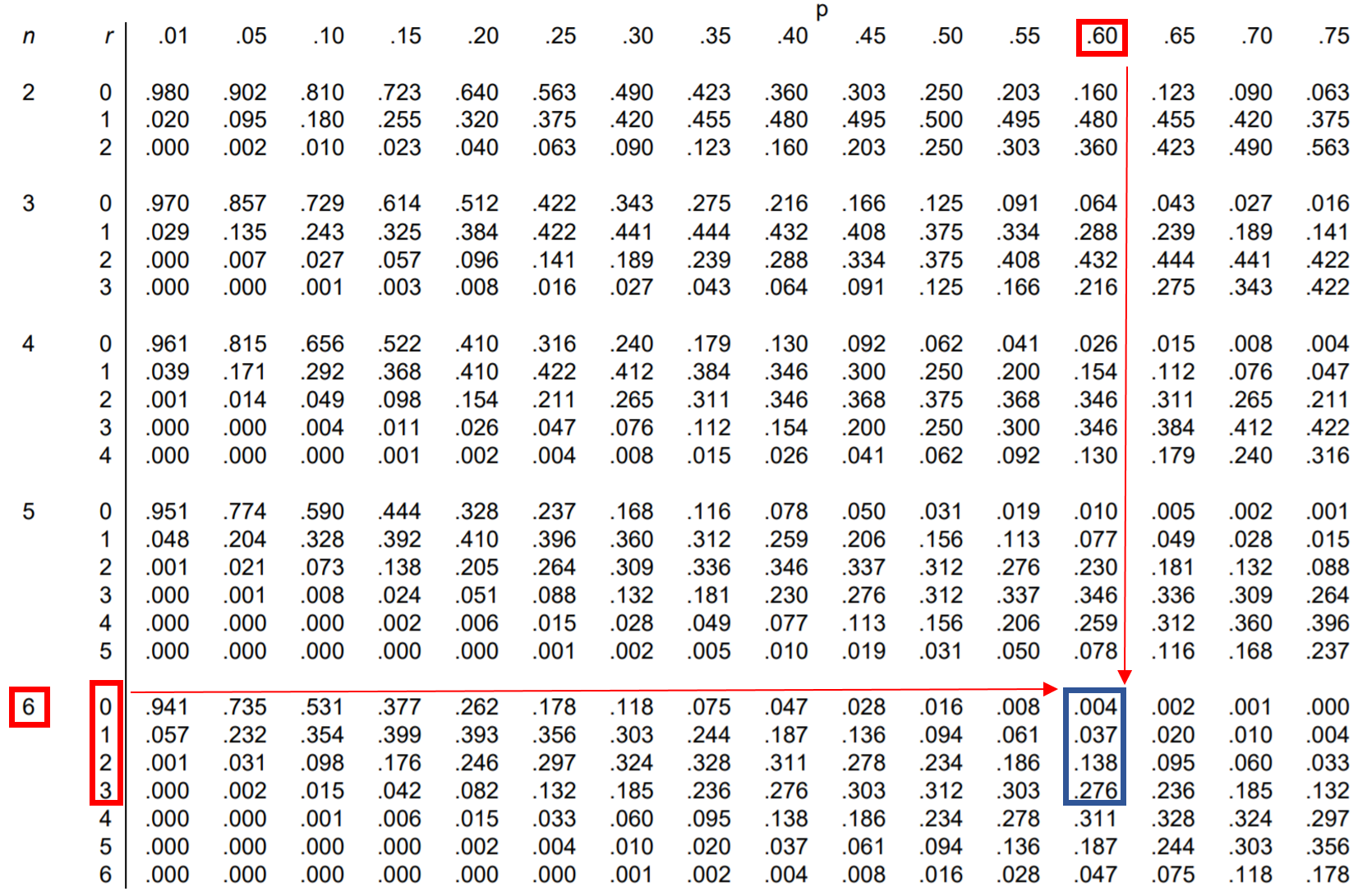
Dari tabel, P(kurang dari 4) = .004 + .037 + .138 + .276 = 0.455 .

Peluang Jessica melakukan lemparan bebas kurang dari 4 adalah 0,455 .

Contoh 3

Pertanyaan: Jessica melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 6 kali lemparan bebas, berapa peluang dia melakukan 4 kali lemparan bebas atau lebih?

Untuk mencari probabilitas ini, kita harus menambahkan probabilitas berikut:

P(hasil 4 atau lebih) = P(hasil 4) + P(hasil 5) + P(hasil 6)

Jadi, kita dapat mencari masing-masing dari ketiga probabilitas ini dalam tabel distribusi binomial dan menjumlahkannya:

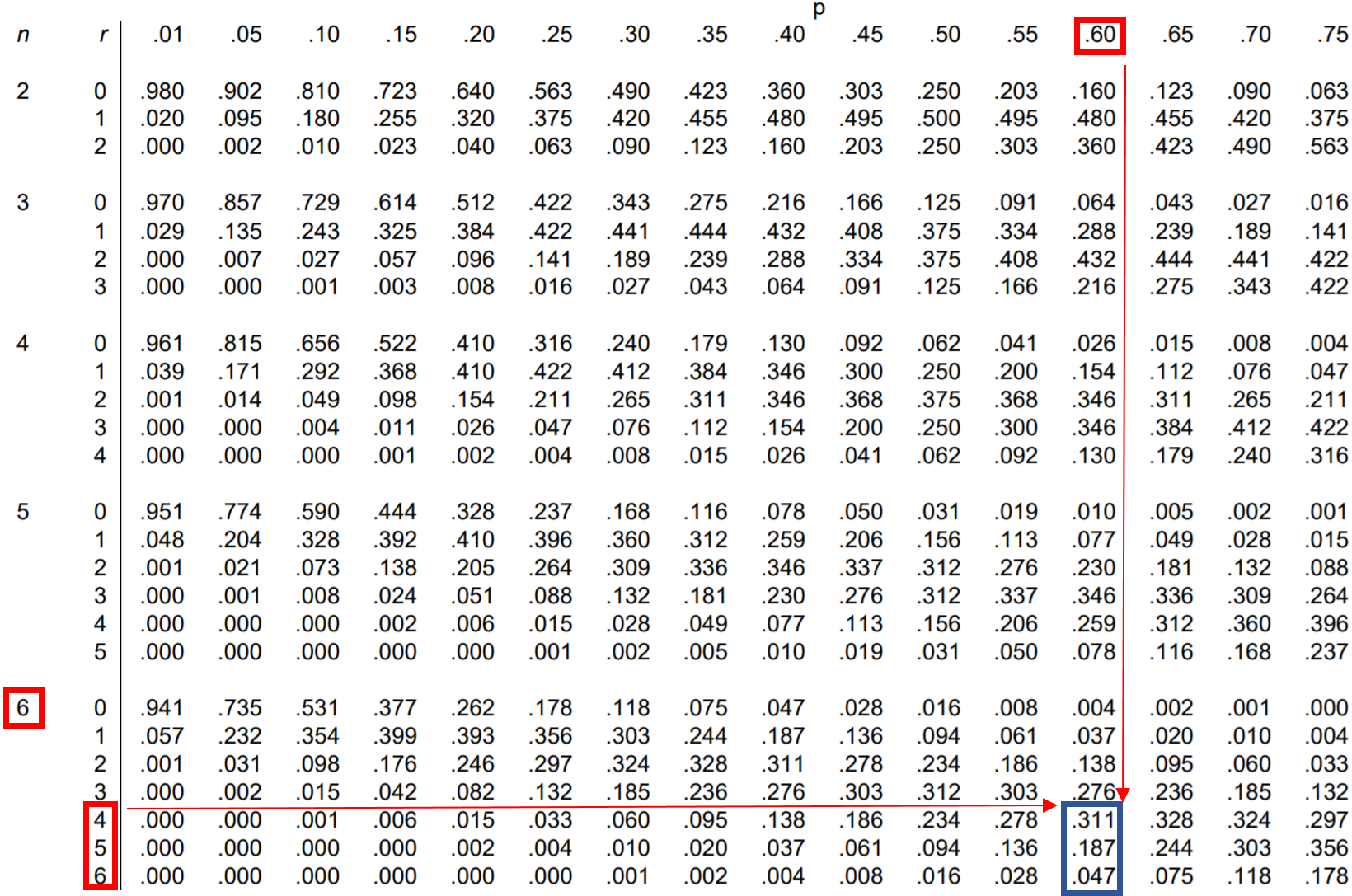
Dari tabel, P(menghasilkan 4 atau lebih) = .311 + .187 + .047 = 0.545 .

Peluang Jessica melakukan 4 kali lemparan bebas atau lebih adalah 0,545 .