Cara mencari nilai kritis t pada kalkulator ti-84

Saat Anda melakukan uji-t, Anda mendapatkan statistik uji. Untuk menentukan apakah hasil uji-t signifikan secara statistik, Anda dapat membandingkan statistik uji dengan nilai kritis T. Jika nilai absolut statistik uji lebih besar dari nilai kritis T, maka hasil pengujian signifikan secara statistik.

Untuk mencari nilai kritis T pada kalkulator TI-84, Anda dapat menggunakan fungsi berikut:

invT(probabilitas, v)

Emas:

• probabilitas: tingkat signifikansi
• v: derajat kebebasan

Anda dapat mengakses fungsi ini pada kalkulator TI-84 dengan menekan 2nd lalu menekan vars . Ini akan membawa Anda ke layar DISTR tempat Anda kemudian dapat menggunakan invT() :

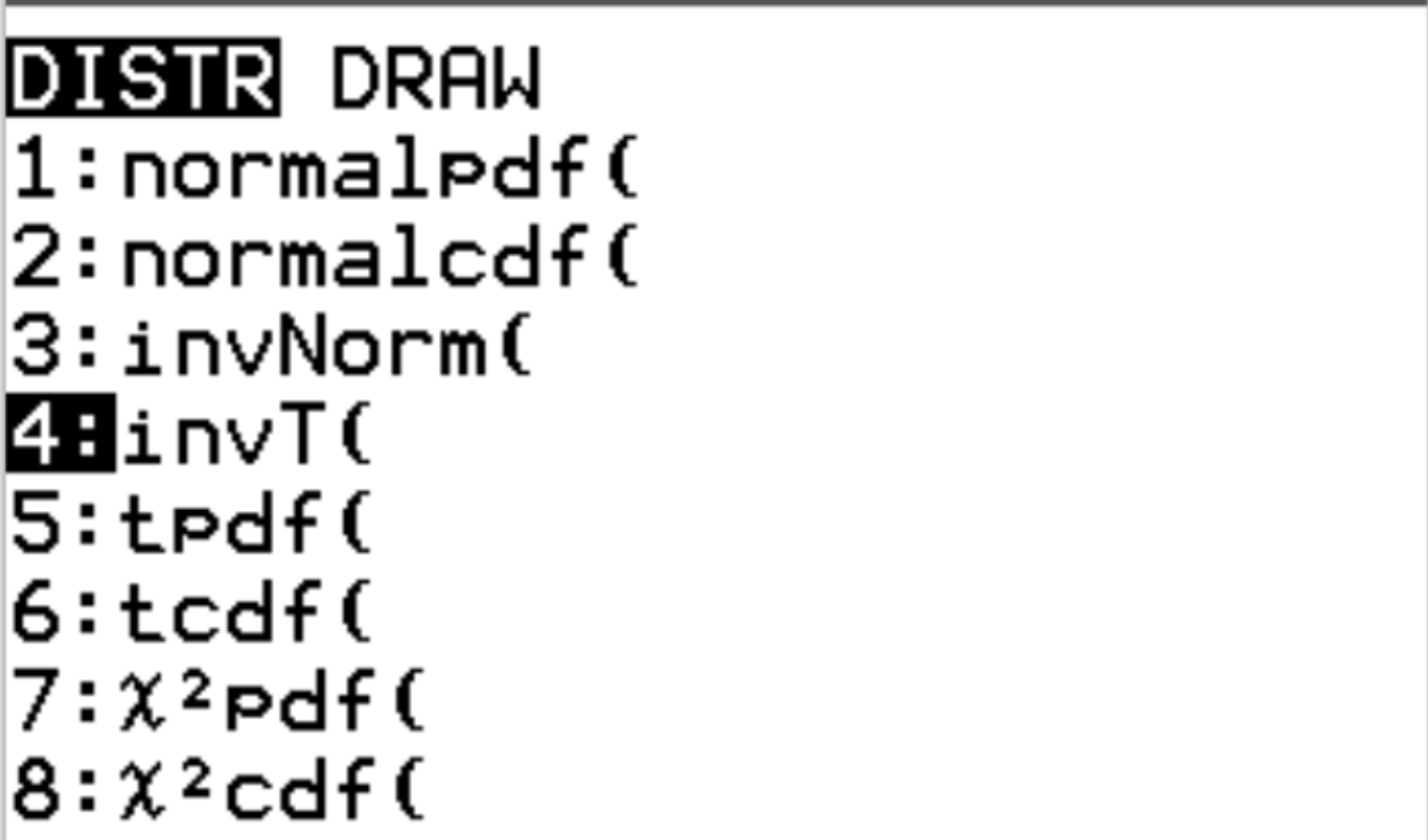
Tutorial ini membagikan beberapa contoh penggunaan fungsi invT() untuk mencari nilai kritis T pada kalkulator TI-84.

Contoh 1: nilai kritis T untuk pengujian di sebelah kiri

Soal: Tentukan nilai kritis T uji kiri dengan tingkat signifikansi 0,05 dan derajat kebebasan = 11.

Jawaban: invT(.05, 11) = -1.7959

Interpretasi: Jika statistik uji-t kurang dari -1,7959 , maka hasil pengujian tersebut signifikan secara statistik pada α = 0,05.

Contoh 2: nilai kritis T untuk uji ekor lurus

Soal: Tentukan nilai kritis T pada uji lateral kanan dengan tingkat signifikansi 0,05 dan derajat bebas = 24.

Jawaban: invT(1-.05, 24) = 1.71088

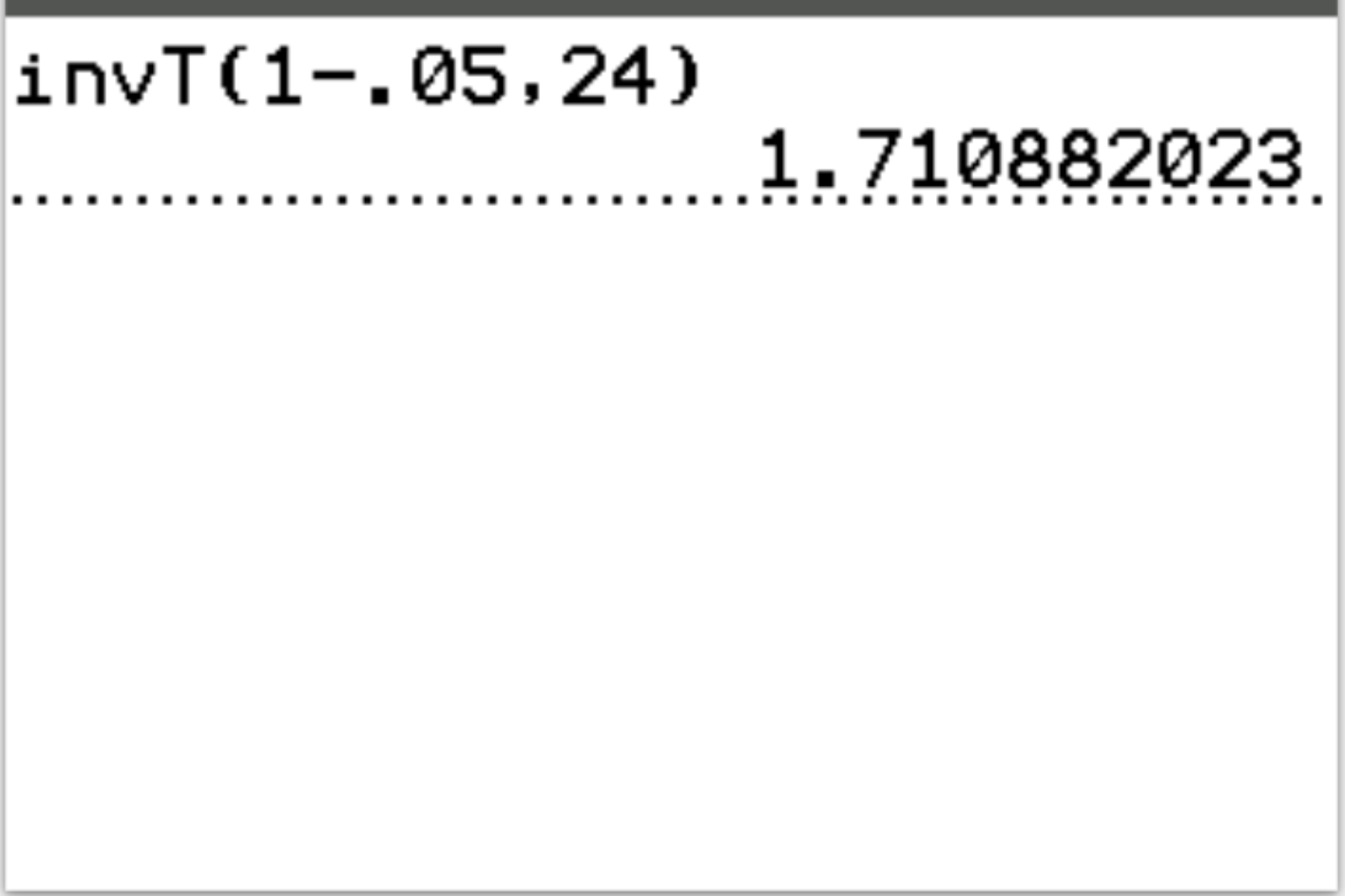
Interpretasi: Jika statistik uji-t lebih besar dari 1,71088 , maka hasil pengujian signifikan secara statistik pada α = 0,05.

Contoh 3: nilai kritis T untuk pengujian dua sisi

Pertanyaan: Tentukan nilai kritis T untuk uji dua sisi dengan tingkat signifikansi 0,05 dan derajat kebebasan = 13.

Jawaban: invT(.05/2, 13) = -2.1604, 2.1604

Interpretasi: Karena ini adalah pengujian dua sisi, kami sebenarnya memiliki dua nilai kritis: -2.1604 dan 2.1604 . Jika statistik uji-t lebih kecil dari -2,1604 atau lebih besar dari 2,1604 , maka hasil pengujian tersebut signifikan secara statistik pada α = 0,05.