Cara mencari nilai p dari skor z di excel

Banyak uji hipotesis dalam statistik menghasilkan statistik uji-z. Setelah kami menemukan statistik uji-z ini, kami biasanya menemukan nilai p yang terkait dengannya. Jika nilai p ini berada di bawah tingkat alfa tertentu (misalnya 0,10, 0,05, 0,01), maka kami menolak hipotesis nol pengujian tersebut dan menyimpulkan bahwa hasil kami signifikan.

Tutorial ini menunjukkan beberapa contoh mencari nilai p dari skor-z di Excel menggunakan fungsi NORM.DIST , yang menggunakan argumen berikut:

NORM.DIST (x, rata-rata, standar_dev, kumulatif)

Emas:

• x adalah skor z yang menarik minat kita.
• mean adalah mean dari distribusi – kita akan menggunakan “0” untuk distribusi normal standar.
• standard_dev adalah simpangan baku distribusi – kita akan menggunakan “1” untuk distribusi normal standar.
• kumulatif mengambil nilai “TRUE” (mengembalikan CDF) atau “FALSE” (mengembalikan PDF) – kita akan menggunakan “TRUE” untuk mendapatkan nilai fungsi distribusi kumulatif.

Mari kita lihat beberapa contoh.

Contoh 1: Menemukan nilai P dari skor Z (uji dua sisi)

Sebuah perusahaan ingin mengetahui apakah baterai jenis baru memiliki umur rata-rata yang berbeda dengan baterai standar saat ini, yang memiliki umur rata-rata 18 jam. Dalam sampel acak 100 baterai baru, mereka menemukan bahwa masa pakai rata-rata adalah 19 jam dengan deviasi standar 4 jam.

Lakukan uji hipotesis dua sisi menggunakan tingkat alpha 0,05 untuk mengetahui apakah rata-rata umur baterai baru berbeda dengan rata-rata umur baterai standar saat ini.

Langkah 1: Nyatakan hipotesisnya.

Hipotesis nol (H ₀ ): μ = 18

Hipotesis alternatif: (Ha): μ ≠ 18

Langkah 2: Temukan statistik uji-z.

Statistik uji z = (x-μ) / (s/√n) = (19-18) / (4/√100) = 2,5

Langkah 3: Temukan nilai p dari statistik uji-z menggunakan Excel.

Untuk mencari nilai p untuk z = 2.5, kita akan menggunakan rumus berikut di Excel: =1 – NORM.DIST(2.5, 0, 1, TRUE)

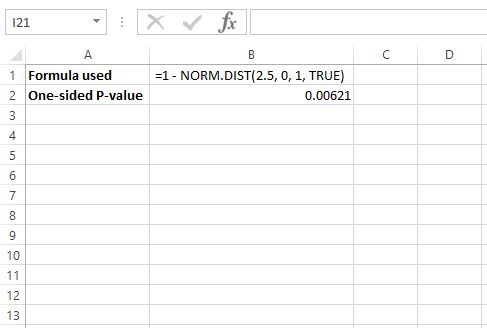
Hal ini menunjukkan bahwa nilai p satu sisi adalah 0,00621 , namun karena kita melakukan pengujian dua sisi, kita perlu mengalikan nilai ini dengan 2, sehingga nilai p menjadi 0,00612 * 2 = 0,01224 .

Langkah 4: Tolak atau jangan tolak hipotesis nol.

Karena nilai p sebesar 0,01224 lebih kecil dari tingkat alfa yang dipilih sebesar 0,05 , kami menolak hipotesis nol. Kami memiliki cukup bukti untuk mengatakan bahwa rata-rata masa pakai baterai baru berbeda secara signifikan dari rata-rata masa pakai baterai standar saat ini.

Contoh 2: Menemukan nilai P dari skor Z (tes satu sisi)

Seorang ahli botani memperkirakan bahwa tinggi rata-rata tanaman tertentu kurang dari 14 inci. Dia secara acak memilih 30 tanaman dan mengukurnya. Dia menemukan bahwa tinggi rata-rata adalah 13,5 inci dengan standar deviasi 2 inci.

Lakukan uji hipotesis satu sisi menggunakan tingkat alfa 0,01 untuk menentukan apakah rata-rata tinggi tanaman ini sebenarnya kurang dari 14 inci.

Langkah 1: Nyatakan hipotesisnya.

Hipotesis nol (H0): μ≥ 14

Hipotesis alternatif: (Ha): μ < 14

Langkah 2: Temukan statistik uji-z.

Statistik uji z = (x-μ) / (s/√n) = (13,5-14) / (2/√30) = -1,369

Langkah 3: Temukan nilai p dari statistik uji-z menggunakan Excel.

Untuk mencari nilai p untuk z = -1.369, kita akan menggunakan rumus berikut di Excel: =NORM.DIST(-1.369, 0, 1, TRUE)

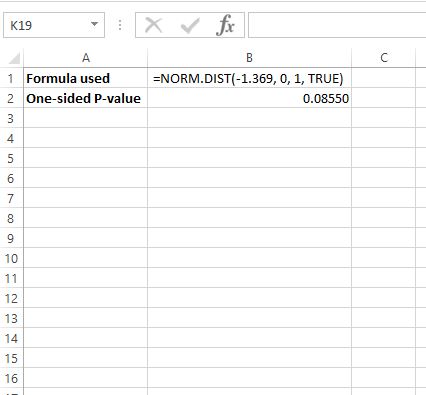
Ini memberitahu kita bahwa nilai p satu sisi adalah 0,08550 .

Langkah 4: Tolak atau jangan tolak hipotesis nol.

Karena nilai p sebesar 0,08550 lebih besar dari tingkat alfa yang dipilih sebesar 0,01 , kami gagal menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa tinggi rata-rata spesies tumbuhan ini kurang dari 14 inci.

Untuk tutorial lebih lanjut tentang statistik di Excel, pastikan untuk membaca daftar lengkap panduan Excel kami .