Cara menghitung nilai p secara manual dari uji t

Salah satu uji yang paling umum digunakan dalam statistik adalah uji-t , yang sering digunakan untuk menentukan apakah rata-rata suatu populasi sama dengan nilai tertentu.

Misalnya, kita ingin mengetahui apakah tinggi rata-rata spesies tanaman tertentu sama dengan 15 inci. Untuk mengujinya, kita dapat mengumpulkan sampel acak sebanyak 20 tanaman, mencari mean sampel dan deviasi standar sampel, dan melakukan uji-t untuk menentukan apakah tinggi rata-rata sebenarnya adalah 15 inci.

Hipotesis nol dan alternatif dari pengujian tersebut adalah sebagai berikut:

H ₀ : µ = 15

H _a : µ ≠ 15

Rumus statistik uji adalah:

t = ( X -μ) / (s/ √n )

dimana x adalah mean sampel, μ adalah mean hipotetis (dalam contoh kita adalah 15), s adalah deviasi standar sampel, dan n adalah ukuran sampel.

Setelah kita mengetahui nilai t , kita dapat menggunakan perangkat lunak statistik atau kalkulator online untuk mencari nilai p yang sesuai. Jika nilai p berada di bawah tingkat alfa tertentu (pilihan umum adalah 0,01, 0,05, dan 0,10), maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa rata-rata tinggi tanaman tidak sama dengan 15 inci.

Namun, dimungkinkan juga untuk memperkirakan nilai p pengujian secara manual menggunakan tabel distribusi t . Pada artikel ini kami akan menjelaskan cara melakukan ini.

Contoh: Perhitungan nilai p secara manual dari uji-t

Soal : Bob ingin mengetahui apakah tinggi rata-rata suatu spesies tumbuhan tertentu sama dengan 15 inci. Untuk mengujinya, ia mengumpulkan sampel acak dari 20 tanaman dan menemukan bahwa rata-rata sampel adalah 14 inci dan simpangan baku sampel adalah 3 inci. Lakukan uji-t menggunakan tingkat alfa 0,05 untuk menentukan apakah rata-rata tinggi populasi sebenarnya adalah 15 inci.

Larutan:

Langkah 1: Nyatakan hipotesis nol dan hipotesis alternatif.

H ₀ : µ = 15

H _a : µ ≠ 15

Langkah 2: Temukan statistik pengujian.

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1,49

Langkah 3: Temukan nilai p untuk statistik uji.

Untuk mencari nilai p secara manual, kita perlu menggunakan tabel distribusi t dengan derajat kebebasan n-1. Dalam contoh kita, ukuran sampel kita adalah n = 20, jadi n-1 = 19.

Pada tabel distribusi t di bawah, kita perlu melihat baris yang berhubungan dengan “19” di sisi kiri dan mencoba mencari nilai absolut dari statistik pengujian kita 1.49 .

Perhatikan bahwa 1.49 tidak muncul dalam tabel, tetapi berada di antara dua nilai 1.328 dan 1.729 .

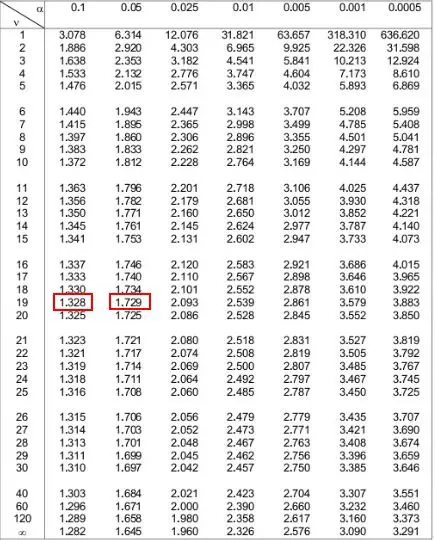
Kemudian kita dapat melihat dua level alfa di bagian atas tabel yang sesuai dengan kedua angka tersebut. Kita melihat bahwa keduanya adalah 0.1 dan 0.05 .

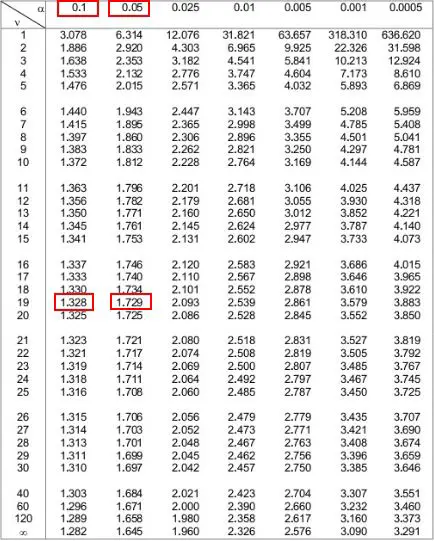
Artinya nilai p untuk uji satu sisi adalah antara 0,1 dan 0,05. Sebut saja 0,075. Karena uji-t kita adalah dua sisi, kita perlu mengalikan nilai ini dengan 2. Jadi, perkiraan nilai p kita adalah 0,075 * 2 = 0,15 .

Langkah 4: Buatlah kesimpulan.

Karena nilai p ini tidak lebih rendah dari tingkat alfa yang dipilih sebesar 0,05, kami tidak dapat menolak hipotesis nol. Oleh karena itu, kami tidak memiliki cukup bukti untuk mengatakan bahwa tinggi rata-rata sebenarnya dari spesies tanaman ini selain 15 inci.

Periksa hasilnya dengan kalkulator

Kita dapat memasukkan statistik uji -t dan derajat kebebasan ke dalam kalkulator nilai p online untuk melihat seberapa dekat perkiraan nilai p kita dengan nilai p sebenarnya:

Nilai p sebenarnya adalah 0.15264 , yang cukup dekat dengan perkiraan nilai p kami sebesar 0.15 .

Kesimpulan

Kita melihat di artikel ini bahwa dimungkinkan untuk memperkirakan nilai p dari uji-t secara manual menggunakan tabel distribusi-t. Namun, dalam sebagian besar skenario, Anda tidak perlu menghitung nilai p secara manual dan Anda dapat menggunakan perangkat lunak statistik seperti R dan Excel atau kalkulator online untuk menemukan nilai p yang tepat dari pengujian tersebut.

Dalam kebanyakan kasus, terutama dalam studi statistik dan eksperimen yang ketat, Anda akan ingin menggunakan kalkulator untuk menemukan nilai p yang tepat dari uji-t agar setepat mungkin, namun ada baiknya untuk mengetahui bahwa Anda selalu dapat memperkirakan secara manual. nilai p dari uji-t jika Anda benar-benar membutuhkannya.