Variasi dalam kelompok atau antar kelompok dalam anova
ANOVA satu arah digunakan untuk menentukan apakah rata-rata dari tiga atau lebih kelompok independen adalah sama atau tidak.
ANOVA satu arah menggunakan hipotesis nol dan hipotesis alternatif berikut:
- H 0 : Semua mean grup adalah sama.
- H A : Setidaknya rata-rata satu kelompok berbeda dengan kelompok lainnya.
Setiap kali Anda melakukan ANOVA satu arah, Anda akan mendapatkan tabel ringkasan seperti berikut:
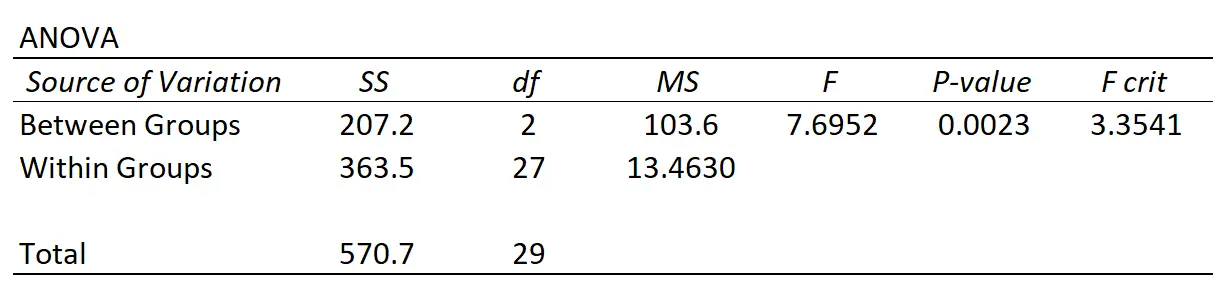
Kita dapat melihat bahwa ada dua sumber variasi berbeda yang diukur oleh ANOVA:
Variasi antar kelompok : variasi total antara rata-rata masing-masing kelompok dan rata-rata keseluruhan.
Variasi dalam kelompok : total variasi nilai individu dalam setiap kelompok dan rata-rata kelompoknya.
Jika variasi antar kelompok relatif tinggi terhadap variasi dalam kelompok, maka statistik F dari ANOVA akan lebih tinggi dan nilai p yang sesuai akan lebih rendah, sehingga hipotesis nol lebih besar kemungkinannya untuk ditolak. rata-rata kelompok adalah sama.
Contoh berikut menunjukkan cara menghitung variasi antar kelompok dan variasi dalam kelompok untuk ANOVA satu arah dalam praktiknya.
Contoh: Menghitung variasi dalam suatu kelompok dan antar kelompok dalam ANOVA
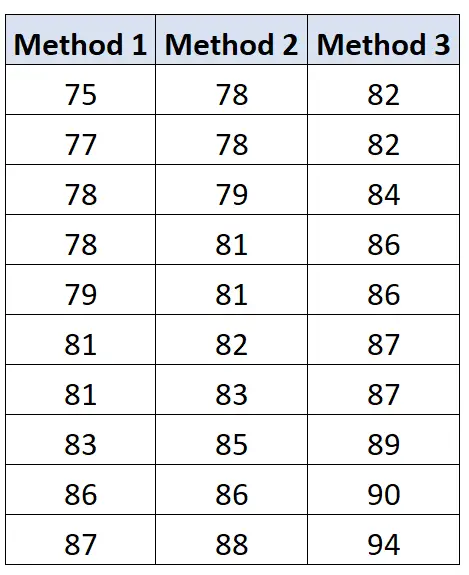
Misalkan kita ingin menentukan apakah tiga metode belajar yang berbeda menghasilkan rata-rata nilai ujian yang berbeda. Untuk mengujinya, kami merekrut 30 siswa dan secara acak menugaskan 10 siswa untuk menggunakan metode belajar yang berbeda.
Hasil ujian siswa pada masing-masing kelompok ditunjukkan di bawah ini:
Kita dapat menggunakan rumus berikut untuk menghitung variasi antar kelompok :
Variasi antar kelompok = Σn j (X j – X ..) 2
Emas:
- n j : ukuran sampel kelompok j
- Σ : simbol yang berarti “jumlah”
- X j : rata-rata kelompok j
- X .. : rata-rata keseluruhan
Untuk menghitung nilai ini, pertama-tama kita menghitung rata-rata masing-masing kelompok dan rata-rata keseluruhan:
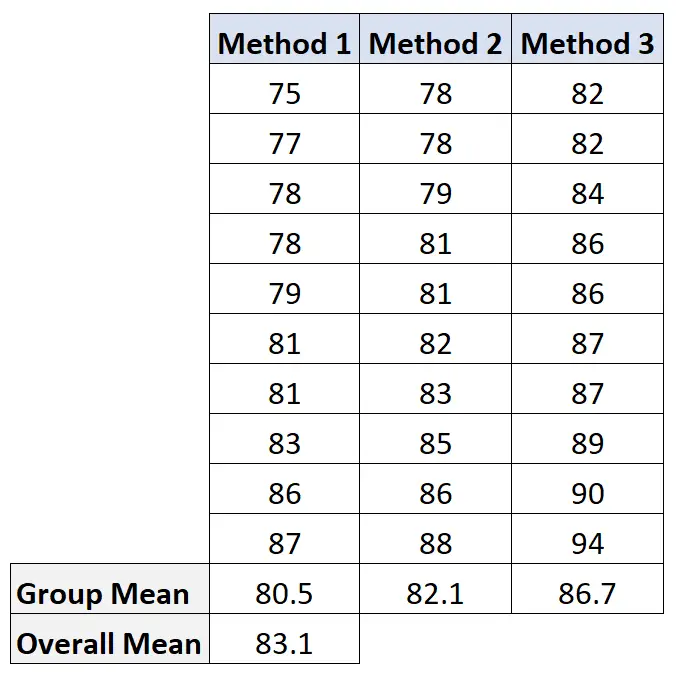
Kemudian kita menghitung variasi antar kelompok sebagai berikut: 10(80.5-83.1) 2 + 10(82.1-83.1) 2 + 10(86.7-83.1) 2 = 207.2 .
Kemudian kita dapat menggunakan rumus berikut untuk menghitung variasi dalam grup :
Variasi intra-grup : Σ(X ij – X j ) 2
Emas:
- Σ : simbol yang berarti “jumlah”
- X ij : observasi ke-i kelompok j
- X j : rata-rata kelompok j
Dalam contoh kami, kami menghitung variasi dalam grup sebagai:
Grup 1: (75-80.5) 2 + (77-80.5) 2 + (78-80.5) 2+ (78-80.5) 2+ (79-80.5) 2+ (81-80.5) 2+ (81-80.5) 2+ (83-80.5) 2+ (86-80.5) 2+ (87-80,5) 2 = 136,5
Grup 2: (78-82.1) 2 + (78-82.1) 2 + (79-82.1) 2 + (81-82.1) 2+ (81-82.1) 2+ (82-82.1) 2 + (83-82.1) 2 + (85-82.1) 2 + (86-82.1) 2 + (88-82.1) 2 = 104.9
Grup 3: (82-86.7) 2 + (82-86.7) 2 + (84-86.7) 2+ (86-86.7) 2+ (86-86.7) 2+ (87-86.7) 2+ (87-86.7) 2+ (89-86.7) 2+ (90-86.7) 2+ (94-86.7) 2 = 122.1
Variasi dalam grup: 136,5 + 104,9 + 122,1 = 363,5
Jika kita menggunakan software statistik untuk melakukan ANOVA satu arah menggunakan dataset ini, kita akan mendapatkan tabel ANOVA berikut:
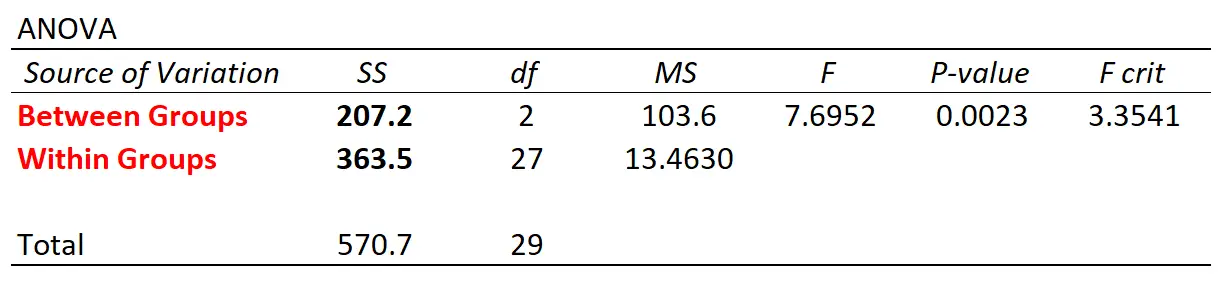
Perhatikan bahwa nilai variasi antar grup dan dalam grup cocok dengan yang kami hitung secara manual.
Statistik F keseluruhan dalam tabel adalah cara untuk mengukur hubungan antara variasi antar kelompok dan variasi dalam kelompok.
Semakin besar statistik F, semakin besar rata-rata variasi antar kelompok dibandingkan dengan variasi dalam kelompok.
Jadi, semakin besar statistik F, semakin jelas terlihat adanya perbedaan rata-rata antar kelompok.
Kita dapat melihat dalam contoh ini bahwa nilai p yang sesuai dengan statistik F 7,6952 adalah 0,0023 .
Karena nilai ini kurang dari α = 0,05, kami menolak hipotesis nol ANOVA dan menyimpulkan bahwa ketiga teknik belajar tidak menghasilkan nilai ujian yang sama.
Sumber daya tambahan
Tutorial berikut memberikan informasi tambahan tentang model ANOVA:
Pengantar ANOVA Satu Arah
Bagaimana menginterpretasikan nilai F dan nilai P dalam ANOVA
Panduan Lengkap: Cara Melaporkan Hasil ANOVA
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya