Panduan lengkap: desain faktorial 2×4

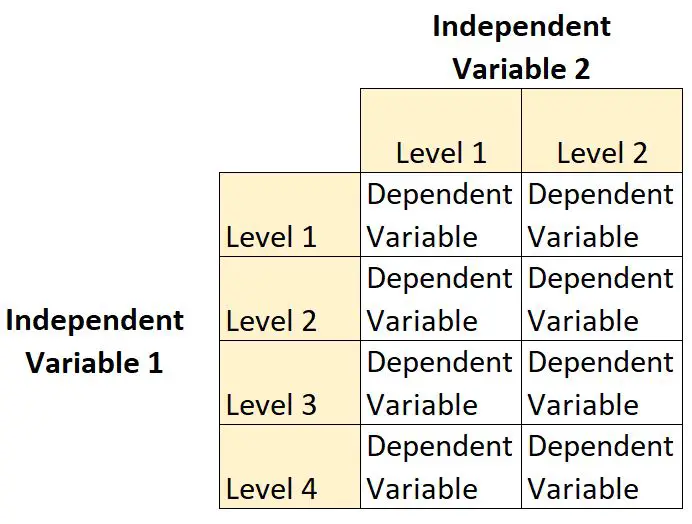
Desain faktorial 2×4 adalah jenis desain eksperimen yang memungkinkan peneliti memahami pengaruh dua variabel independen terhadap satu variabel dependen.

Dalam jenis desain ini, satu variabel independen memiliki dua level dan variabel independen lainnya memiliki empat level.

Misalnya, seorang ahli botani ingin memahami pengaruh sinar matahari (tidak ada, rendah, sedang, atau tinggi) dan frekuensi penyiraman (setiap hari atau mingguan) terhadap pertumbuhan spesies tanaman tertentu.

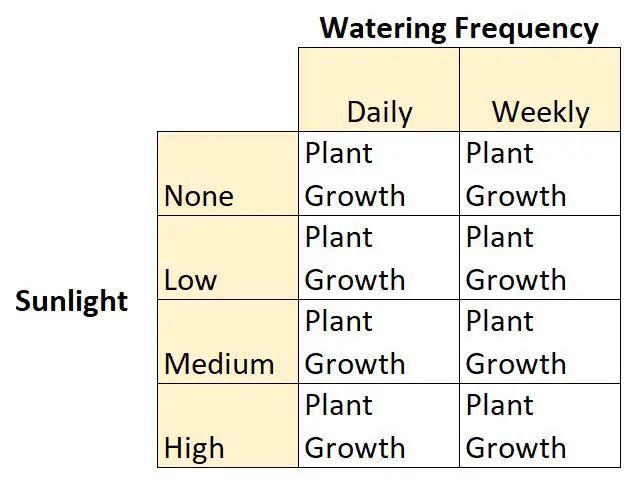
Ini adalah contoh desain faktorial 2×4 karena terdapat dua variabel bebas, satu dengan dua tingkat dan satu lagi dengan empat tingkat:

• Variabel Independen #1: Sinar matahari
  • Level: Tidak Ada, Rendah, Sedang, Tinggi
• Variabel bebas #2: Frekuensi penyiraman
  • Level: harian, mingguan

Dan ada variabel terikat: pertumbuhan tanaman.

Tujuan dari desain faktorial 2×4

Desain faktorial 2×4 memungkinkan untuk menganalisis efek berikut:

Pengaruh utama: Ini adalah pengaruh yang dimiliki satu variabel independen terhadap variabel dependen.

Misalnya, dalam skenario sebelumnya, kita dapat menganalisis efek utama berikut:

• Pengaruh utama sinar matahari terhadap pertumbuhan tanaman.
  • Pertumbuhan rata-rata semua tanaman yang tidak mendapat sinar matahari.
  • Rata-rata pertumbuhan seluruh tanaman yang mendapat sinar matahari rendah.
  • Pertumbuhan rata-rata semua tanaman yang mendapat sinar matahari rata-rata.
  • Rata-rata pertumbuhan seluruh tanaman yang mendapat sinar matahari tinggi.
• Pengaruh utama frekuensi penyiraman terhadap pertumbuhan tanaman.
  • Rata-rata pertumbuhan seluruh tanaman disiram setiap hari.
  • Rata-rata pertumbuhan seluruh tanaman disiram tiap minggu.

Efek interaksi: Terjadi ketika pengaruh satu variabel independen terhadap variabel dependen bergantung pada tingkat variabel independen lainnya.

Misalnya, dalam skenario sebelumnya, kita dapat menganalisis efek interaksi berikut:

• Apakah pengaruh sinar matahari terhadap pertumbuhan tanaman bergantung pada frekuensi penyiraman?
• Apakah pengaruh frekuensi penyiraman terhadap pertumbuhan tanaman bergantung pada sinar matahari?

Cara menganalisis desain faktorial 2×4

Kita dapat melakukan ANOVA dua arah untuk menguji secara formal apakah variabel independen memiliki hubungan yang signifikan secara statistik dengan variabel dependen atau tidak.

Misalnya, kode berikut menunjukkan cara melakukan ANOVA dua arah untuk skenario pabrik hipotetis kami di R:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' None ', ' Low ', ' Medium ', ' High '), each= 10 , times= 2 ),
                 water = rep(c(' Daily ', ' Weekly '), each= 40 , times= 2 ),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 3 744.1 248.04 34.16 < 2e-16 ***
water 1 43.1 43.05 5.93 0.016 *  
sunlight:water 3 195.8 65.27 8.99 1.61e-05 ***
Residuals 152 1103.5 7.26                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Berikut cara menginterpretasikan hasil ANOVA:

Efek utama #1 (sinar matahari) : Nilai p yang terkait dengan sinar matahari adalah <2e-16 . Karena angka ini kurang dari 0,05, berarti paparan sinar matahari mempunyai pengaruh yang signifikan secara statistik terhadap pertumbuhan tanaman.

Efek utama #2 (Air) : Nilai p yang terkait dengan air adalah 0,016 . Karena angka ini kurang dari 0,05, berarti frekuensi penyiraman juga mempunyai pengaruh yang signifikan secara statistik terhadap pertumbuhan tanaman.

Efek interaksi : Nilai p untuk interaksi antara sinar matahari dan air adalah 0,000061 . Karena nilainya kurang dari 0,05 berarti terdapat efek interaksi antara sinar matahari dan air.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang desain dan analisis eksperimental:

Panduan lengkap: desain faktorial 2×2
Panduan lengkap: desain faktorial 2×3
Apa itu ANOVA Faktorial?