Desil

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Pada artikel ini kami menjelaskan apa itu desil dan cara menghitungnya. Anda juga akan menemukan beberapa contoh perhitungan desil langkah demi langkah yang diselesaikan dan, sebagai tambahan, Anda akan dapat menghitung desil sampel statistik apa pun dengan kalkulator online.

Apa itu desil?

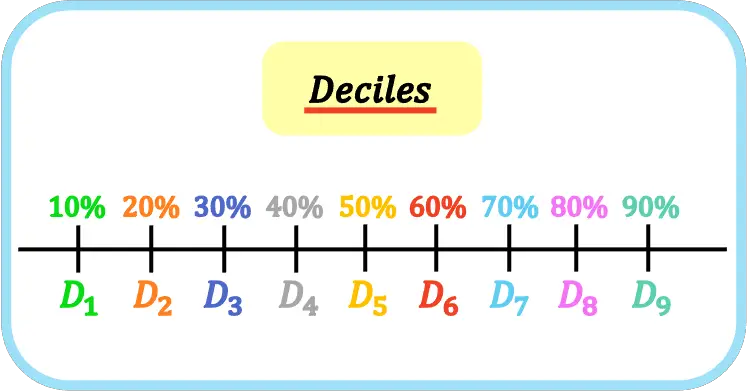
Dalam statistik, desil adalah sembilan nilai yang membagi sekumpulan data terurut menjadi sepuluh bagian yang sama. Sehingga desil pertama, kedua, ketiga,… mewakili 10%, 20%, 30%,… dari sampel atau populasi.

Misalnya, nilai desil keempat lebih tinggi dari 40% data, namun lebih rendah dari data lainnya.

Desil diwakili oleh huruf kapital D dan indeks desil, yaitu desil pertama adalah D ₁ , desil kedua adalah D ₂ , desil ketiga adalah D ₃ , dan seterusnya.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung desil untuk kumpulan data apa pun.

Perlu diperhatikan bahwa desil adalah ukuran posisi non-pusat seperti halnya kuartil, kuintil, dan persentil. Anda dapat memeriksa arti dari masing-masing jenis kuantil ini di situs web kami.

Selain itu, desil kelima setara dengan median dan kuartil kedua, karena keduanya membagi seluruh kumpulan data menjadi dua bagian yang sama besar.

Cara menghitung desil

Untuk menghitung posisi desil suatu rangkaian data statistik, kalikan angka desil dengan jumlah total data ditambah satu dan bagi hasilnya dengan sepuluh.

Oleh karena itu rumus desilnya adalah:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Harap diperhatikan: rumus ini memberitahu kita posisi desil, bukan nilai desil. Desil adalah data yang terletak pada posisi yang diperoleh rumus.

Namun terkadang hasil rumus ini akan memberikan kita angka desimal, oleh karena itu kita harus membedakan dua kasus tergantung apakah hasilnya berupa angka desimal atau bukan:

Jika hasil rumusnya berupa bilangan tanpa bagian desimal , maka desil adalah data yang terletak pada posisi yang disediakan rumus di atas.
Jika hasil rumusnya berupa bilangan dengan bagian desimal , maka nilai desilnya dihitung menggunakan rumus berikut:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Dimana x _i dan x _i+1 adalah bilangan posisi di mana letak bilangan yang diperoleh rumus pertama, dan d adalah bagian desimal dari bilangan yang diperoleh rumus pertama.

Sekarang Anda mungkin berpikir bahwa mendapatkan desil sampel statistik itu rumit, namun dalam praktiknya cukup sederhana. Jika Anda membaca dua contoh berikut, Anda pasti akan lebih memahaminya.

Catatan : Komunitas ilmiah belum sepenuhnya sepakat tentang cara menghitung desil, jadi Anda dapat menemukan buku statistik yang menjelaskannya sedikit berbeda.

Contoh perhitungan desil

Seperti yang Anda lihat di atas, penghitungan desil bergantung pada apakah bilangan yang diberikan rumus pertama adalah desimal atau bukan, itulah sebabnya kami telah menyiapkan dua contoh penyelesaian di bawah ini, satu untuk setiap kasus. Bagaimanapun, ingatlah bahwa jika Anda memiliki pertanyaan tentang komposisi desil, Anda dapat menanyakannya di komentar.

Contoh 1

Diketahui data berikut, dari yang terkecil hingga yang terbesar, tentukan desil pertama, ketiga, dan kedelapan dari sampel tersebut.

Data pada latihan ini sudah terurut, jadi tidak perlu diubah urutannya, jika tidak kita harus mengurutkan data dari yang terkecil hingga yang terbesar terlebih dahulu.

Seperti yang sudah dijelaskan di atas, rumus yang memungkinkan untuk mencari posisi desil adalah sebagai berikut:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

Besar sampel pada latihan ini adalah 29 observasi, jadi untuk menghitung posisi desil pertama harus substitusikan 29 untuk n dan 1 untuk k :

$\cfrac{1\cdot (29+1)}{10}=3\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_1=85$

Hasil rumusnya adalah 3, jadi desil pertama akan berada di posisi ketiga dari daftar terurut, dan nilainya sama dengan 85.

Sekarang kita menerapkan prosedur yang sama lagi tetapi dengan desil ketiga. Kami menggunakan rumus mengganti k dengan 3:

$\cfrac{3\cdot (29+1)}{10}=9\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_3=97$

Oleh karena itu, desil ketiga akan menjadi unsur pada posisi kesembilan, yaitu 97.

Terakhir, kita melakukan proses yang sama tetapi memberi angka 8 pada rumus untuk menentukan desil kedelapan:

$\cfrac{8\cdot (29+1)}{10}=24\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_8=131$

Desil kedelapan adalah angka pada posisi 24 dari daftar data yang diurutkan, sehingga desil kedelapan adalah 131.

Contoh 2

Dari data pada tabel berikut, hitunglah desil 4, 7 dan 9.

Seperti pada contoh sebelumnya, untuk mendapatkan posisi desil harus menggunakan rumus berikut:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

Dalam hal ini ukuran sampelnya adalah 42, jadi untuk mencari posisi desil keempat Anda harus mengganti parameter n dengan 42 dan k dengan 4:

$\cfrac{4\cdot (42+1)}{10}=17,2$

Namun kali ini kita mendapatkan bilangan desimal dari rumus tersebut, jadi kita perlu menerapkan rumus berikut untuk menghitung desil pastinya:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Angka yang diperoleh dari rumus pertama adalah 17,2, jadi desil keempat berada di antara desil ketujuh belas dan kedelapan belas, yaitu masing-masing 109 dan 112. Jadi, x _i adalah 109, x _{i+ 1} adalah 112 dan d adalah bagian desimal. dari jumlah yang diperoleh yaitu 0,2.

$D_4=109+0,2\cdot (112-109)=109,6$

Kami mengulangi proses yang sama untuk menemukan desil ketujuh. Kita hitung dulu posisi desilnya:

$\cfrac{7\cdot (42+1)}{10}=30,1$

Dari rumus tersebut diperoleh angka 30,1 yang artinya desilnya berada di antara posisi 30 dan 31 yang nilainya 154 dan 159. Oleh karena itu, perhitungan desil eksaknya adalah:

$D_7=154+0,1\cdot (159-154)=154,5$

Terakhir, kita terapkan kembali cara yang sama untuk mendapatkan desil kesembilan. Kami menentukan posisi desil:

$\cfrac{9\cdot (42+1)}{10}=38,7$

Angka yang diperoleh adalah desimal antara 38 dan 39, yang posisinya sesuai dengan nilai 189 dan 196. Jadi perhitungan desil 9 adalah:

$D_9=189+0,7\cdot (196-189)=193,9$

Kalkulator Desil

Masukkan kumpulan data statistik ke dalam kalkulator di bawah ini untuk menghitung desil. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Desil dalam data yang dikelompokkan

Untuk menghitung desil ketika data dikelompokkan ke dalam interval , pertama-tama kita perlu mencari interval atau bin tempat desil tersebut berada menggunakan rumus berikut:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,3,4,5,6,7,8,9$

Oleh karena itu, desil tersebut akan berada dalam interval yang frekuensi absolutnya lebih besar daripada angka yang diperoleh pada persamaan sebelumnya.

Dan setelah kita mengetahui interval desil tersebut, kita harus menerapkan rumus berikut untuk mencari nilai pasti dari desil tersebut:

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4,5,6,7,8,9$

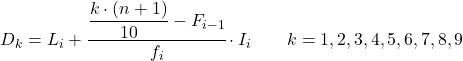
Emas:

L _i adalah batas bawah interval di mana desil tersebut berada.
n adalah jumlah total data statistik.
F _i-1 adalah frekuensi absolut kumulatif dari interval sebelumnya.
f _i adalah frekuensi absolut dari interval di mana desil tersebut berada.
I _i adalah lebar interval desil.

Agar Anda dapat melihat bagaimana hal ini dilakukan, di bawah ini Anda memiliki latihan yang telah selesai di mana desil 3, 5 dan 8 dari data berikut yang dikelompokkan berdasarkan interval dihitung.

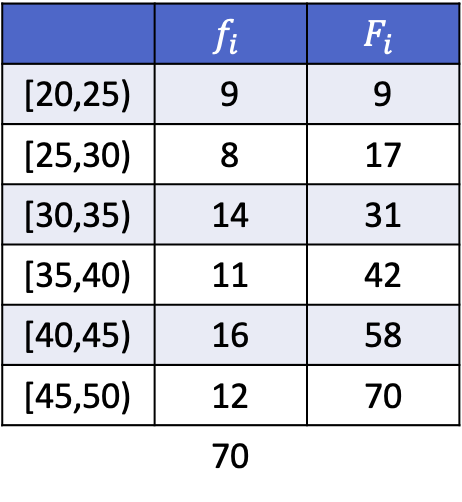
Karena datanya dikelompokkan, penghitungan setiap desil terdiri dari dua langkah: pertama, cari interval di mana desil tersebut berada, kemudian hitung nilai pasti desil tersebut. Oleh karena itu, kita mencari interval desil ketiga:

$\cfrac{k\cdot (n+1)}{10}$

$\cfrac{3\cdot (70+1)}{10} =21,3 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [30,35)$

Interval desil adalah interval yang frekuensi kumulatif absolutnya lebih besar dari 21,3, dan dalam hal ini adalah interval [30,35) yang frekuensi kumulatif absolutnya adalah 31. Sekarang setelah kita mengetahui interval desil, kita terapkan rumus berikut untuk mencari nilai pasti desil:

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i$

$D_3=30+ \cfrac{\displaystyle\frac{3\cdot (70+1)}{10}-17}{14}\cdot 5=31,54$

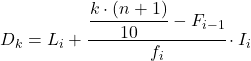
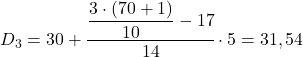
Sekarang kita harus menerapkan kembali metode tersebut untuk mendapatkan desil kelima. Pertama-tama kita tentukan interval letaknya:

$\cfrac{5\cdot (70+1)}{10} =35,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [35,40)$

Hasil 35 berarti berada pada interval [35,40) tetapi bukan karena terdapat 35 pada ekspresi intervalnya, namun karena akumulasi frekuensi absolutnya (42) adalah yang paling tinggi. Dan setelah intervalnya teridentifikasi, kami menerapkan rumus kedua dari proses tersebut:

$D_5=35+ \cfrac{\displaystyle\frac{5\cdot (70+1)}{10}-31}{11}\cdot 5=37,05$

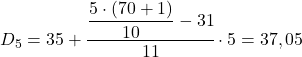
Akhirnya, kita menemukan desil kedelapan. Untuk melakukan ini, pertama-tama kita menghitung intervalnya:

$\cfrac{8\cdot (70+1)}{10} =56,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [40,45)$

Frekuensi absolut kumulatif tepat di atas 56,8 adalah 58, sehingga rentang desil kedelapan adalah [40,45). Oleh karena itu, cukup menentukan nilai desil secara pasti:

$D_8=40+ \cfrac{\displaystyle\frac{8\cdot (70+1)}{10}-42}{16}\cdot 5=44,63$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya