Hubungan antara mean & deviasi standar (dengan contoh)
Mean mewakili nilai rata-rata dalam sekumpulan data.
Ini dihitung sebagai berikut:
Rata-rata sampel = Σx i / n
Emas:
- Σ: Simbol yang berarti “jumlah”
- x i : Pengamatan ke- i dalam suatu kumpulan data
- n: jumlah total observasi dalam kumpulan data
Deviasi standar mewakili distribusi nilai dalam kumpulan data relatif terhadap mean.
Ini dihitung sebagai berikut:
Simpangan baku sampel = √ Σ( xi – x batang ) 2 / (n-1)
Emas:
- Σ: Simbol yang berarti “jumlah”
- x i : nilai ke-i dari sampel
- x bar : Arti sampel
- n: Ukuran sampel
Perhatikan hubungan antara mean dan deviasi standar: mean digunakan dalam rumus untuk menghitung deviasi standar .
Faktanya, kita tidak dapat menghitung simpangan baku suatu sampel kecuali kita mengetahui mean sampelnya.
Contoh berikut menunjukkan cara menghitung mean sampel dan deviasi standar sampel untuk kumpulan data dalam praktiknya.
Contoh: Menghitung Mean dan Deviasi Standar untuk Kumpulan Data
Katakanlah kita memiliki kumpulan data berikut yang menunjukkan poin yang dicetak oleh 10 pemain bola basket berbeda:
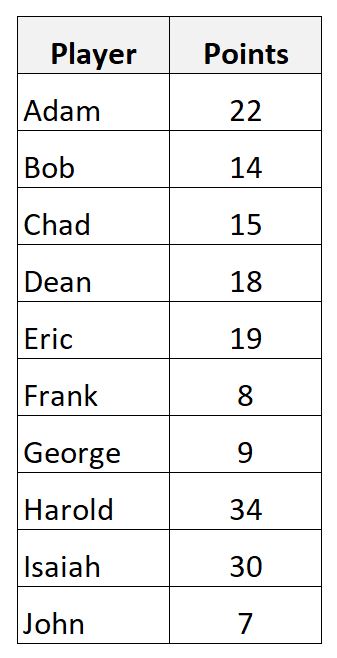Kita dapat menghitung rata-rata sampel poin yang dicetak menggunakan rumus berikut:
- Rata-rata sampel = Σx i / n
- Rata-rata sampel = (22+14+15+18+19+8+9+34+30+7) / 10
- Rata-rata sampel = 17,6
Rata-rata sampel poin yang dicetak adalah 17,6 . Ini mewakili jumlah rata-rata poin yang dicetak di antara semua pemain.
Setelah kita mengetahui mean sampel, kita dapat memasukkannya ke dalam rumus untuk menghitung deviasi standar sampel:
- Simpangan baku sampel = √ Σ( xi – x batang ) 2 / (n-1)
- Simpangan baku sampel = √ ((22-17.6) 2 + (14-17.6) 2 + (15-17.6) 2 + (18-17.6) 2 + (19-17.6) 6) 2 + (8-17.6) 2 + (9 -17.6) 2 + (34-17.6) 2 + (30-17.6) 2 + (7-17.6) 2 ) / (10-1)
- Simpangan baku sampel = 9,08
Simpangan baku sampel adalah 9,08 . Ini mewakili jarak rata-rata antara setiap nilai titik dan rata-rata titik sampel.
Mengetahui mean dan deviasi standar suatu kumpulan data bermanfaat karena setiap metrik memberi tahu kita sesuatu yang berbeda.
Rata-rata memberi kita gambaran di mana letak nilai “pusat” suatu kumpulan data.
Deviasi standar memberi kita gambaran tentang distribusi nilai di sekitar mean dalam suatu kumpulan data. Semakin tinggi nilai standar deviasi, maka semakin tersebar nilai-nilai tersebut dalam suatu sampel.
Dengan mengetahui kedua nilai tersebut, kita bisa belajar banyak tentang sebaran nilai dalam suatu kumpulan data.
Sumber daya tambahan
Tutorial berikut memberikan informasi tambahan tentang mean dan deviasi standar:
Mengapa rata-rata penting dalam statistik?
Mengapa deviasi standar penting dalam statistik?
Cara Menghitung Mean dan Deviasi Standar di Excel
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya