Deviasi standar kuasi

Oleh Benjamin anderson Agustus 3, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu kuasi-standar deviasi dalam statistik dan cara menghitungnya. Jadi, Anda akan menemukan rumus deviasi kuasi-standar, latihan yang diselesaikan, dan, sebagai tambahan, kalkulator online untuk menghitung deviasi kuasi-standar dari kumpulan data mana pun.

Apa itu kuasi-standar deviasi?

Dalam statistik, kuasi-standar deviasi adalah ukuran penyebaran yang menunjukkan variabilitas sampel. Secara khusus, deviasi kuasi-standar sama dengan akar kuadrat dari jumlah kuadrat deviasi dibagi dengan jumlah total titik data dikurangi satu.

Simbol kuasi-standar deviasi adalah σ _n-1 os _n-1 .

Deviasi kuasi-standar juga dapat disebut deviasi kuasi-standar , dan kadang-kadang juga disebut deviasi standar sampel, karena biasanya dihitung menggunakan nilai-nilai dari sampel statistik. Di bawah ini kita akan membahas secara detail tentang perbedaan antara kuasi standar deviasi dan standar deviasi.

Rumus kuasi-standar deviasi

Deviasi kuasi-standar sama dengan akar kuadrat dari jumlah kuadrat deviasi rangkaian data dibagi dengan jumlah observasi dikurangi satu. Oleh karena itu, rumus menghitung kuasi standar deviasi adalah:

Emas:

$\sigma_{n-1}$

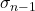
Ini adalah kuasi-standar deviasi.
$x_i$

adalah nilai datanya

$i$

.
$n$

adalah jumlah total data.
$\overline{x}$

adalah rata-rata kumpulan data.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung kuasi-standar deviasi untuk kumpulan data apa pun.

Contoh penghitungan kuasi standar deviasi

Mengingat definisi deviasi kuasi-standar, di bawah ini Anda dapat melihat contoh sederhana cara menghitung deviasi kuasi-standar suatu kumpulan data.

Anggaran suatu perusahaan untuk departemen penelitian dan pengembangannya sangat fluktuatif, karena bergantung pada keuntungan ekonomi yang diperoleh perusahaan pada tahun sebelumnya. Jadi, anggaran untuk bagian ini selama lima tahun terakhir adalah: 3, 6, 2, 9, 4 juta euro. Hitung deviasi kuasi-standar dari rangkaian data ini.

Hal pertama yang perlu kita lakukan untuk menentukan kuasi-standar deviasi adalah menghitung mean aritmatika sampel. Caranya, kita jumlahkan semua data dan membaginya dengan jumlah observasi, yaitu lima:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Selanjutnya, kita terapkan rumus kuasi standar deviasi:

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

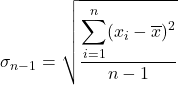
Kami mengganti data ke dalam rumus:

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

Dan terakhir kami menghitung kuasi-standar deviasi:

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

Singkatnya, kuasi standar deviasi sampel data adalah 2,77 juta.

➤ Lihat: Kuasivarian

Kalkulator deviasi kuasi standar

Masukkan kumpulan data statistik ke dalam kalkulator online di bawah ini untuk menghitung deviasi kuasi-standarnya. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Deviasi kuasi standar dan deviasi standar

Terakhir, kita akan melihat perbedaan antara kuasi-standar deviasi dan deviasi standar, karena keduanya adalah ukuran statistik berbeda yang memiliki nama yang sangat mirip dan dihitung dengan cara yang sangat mirip.

Selisih antara simpangan baku kuasi dan simpangan baku adalah penyebut rumusnya. Untuk menghitung simpangan baku kuasi, bagilah dengan n-1, tetapi simpangan baku dihitung dengan membaginya dengan n.

Oleh karena itu, simpangan baku kuasi dan simpangan baku berhubungan secara matematis, karena simpangan baku kuasi setara dengan simpangan baku dikalikan akar kuadrat dari n (jumlah total titik data) per n-1.

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

Dari persamaan sebelumnya kita dapat menyimpulkan bahwa, untuk kumpulan data yang sama, nilai kuasi standar deviasi akan selalu lebih besar dari nilai simpangan baku.

Selain itu, rumus kuasi-standar deviasi sering digunakan untuk menghitung simpangan baku suatu sampel karena dapat menghilangkan bias. Oleh karena itu, simpangan baku kuasi merupakan penduga yang baik untuk simpangan baku populasi. Inilah sebabnya, ketika membuat inferensi statistik dari suatu sampel, sering kali dikatakan bahwa simpangan baku dihitung padahal kenyataannya yang dihitung adalah simpangan baku kuasi.

➤ Lihat: Sifat deviasi standar

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya