Cara mencari mean dari beberapa deviasi standar
Terkadang Anda mungkin ingin mencari rata-rata dari dua atau lebih standar deviasi.
Untuk melakukannya, Anda bisa menggunakan salah satu dari dua rumus berikut, bergantung pada data Anda:
Metode 1: Ukuran sampel yang sama
Jika Anda ingin mencari simpangan baku rata-rata di antara k kelompok dan setiap kelompok memiliki jumlah sampel yang sama, Anda dapat menggunakan rumus berikut:
Rata-rata SD = √ (s 1 2 + s 2 2 + … + s k 2 ) / k
Emas:
- sk : Simpangan baku kelompok ke-k
- k : Jumlah total grup
Metode 2: Ukuran sampel tidak sama
Jika Anda ingin mencari simpangan baku rata-rata di antara k kelompok dan setiap kelompok tidak memiliki jumlah sampel yang sama, Anda dapat menggunakan rumus berikut:
Rata-rata SD = √ ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 + … + (n k -1)s k 2 ) / (n 1 +n 2 + … + n k – J)
Emas:
- n k : Ukuran sampel untuk kelompok ke – k
- sk : Simpangan baku kelompok ke-k
- k : Jumlah total grup
Contoh berikut menunjukkan cara menggunakan setiap rumus dalam praktik.
Metode 1: Menghitung Rata-Rata Deviasi Standar untuk Ukuran Sampel yang Sama
Misalkan kita ingin menghitung rata-rata deviasi standar penjualan selama enam periode penjualan berikut:
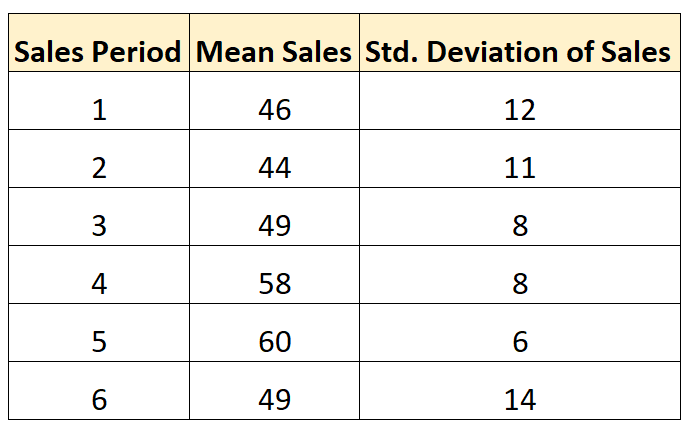
Anggaplah kita melakukan jumlah transaksi penjualan yang sama pada setiap periode penjualan. Kita dapat menggunakan rumus berikut untuk menghitung rata-rata deviasi standar penjualan per periode:
- Simpangan baku rata-rata = √ (s 1 2 + s 2 2 + … + s k 2 ) / k
- Simpangan baku rata-rata = √ (12 2 + 11 2 + 8 2 + 8 2 + 6 2 + 14 2 ) / 6
- Deviasi standar rata-rata = 10,21
Rata-rata simpangan baku penjualan per periode adalah 10,21 .
Metode 2: Rata-rata Deviasi Standar untuk Ukuran Sampel yang Tidak Sama
Misalkan kita ingin menghitung rata-rata deviasi standar penjualan selama enam periode penjualan berikut:
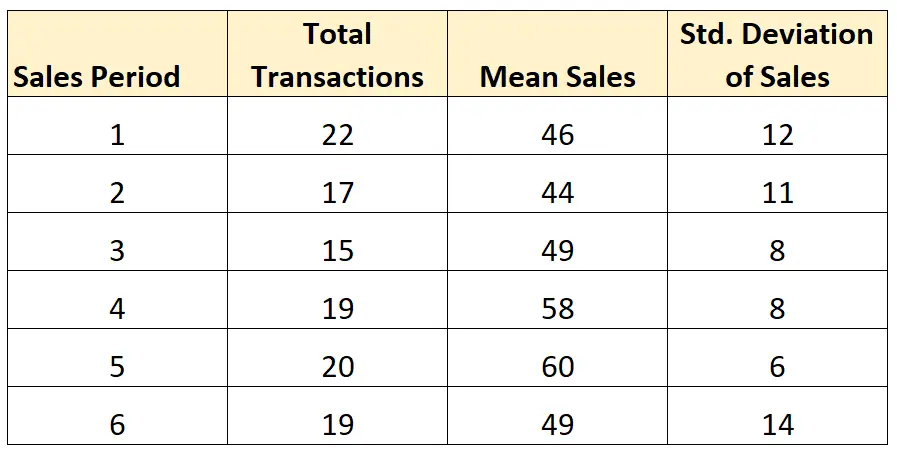
Karena ukuran sampel (total transaksi) tidak sama di setiap periode penjualan, kami akan menggunakan rumus berikut untuk menghitung rata-rata deviasi standar penjualan per periode:
- Rata-rata SD = √ ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 + … + (n k -1)s k 2 ) / (n 1 +n 2 + … + n k – J)
- Rata-rata SD = √ ((21)12 2 + (16)11 2 + (14)8 2 + (18)8 2 + (19)6 2 + (18)14 2 ) / 106
- Berarti SD = 10,29
Rata-rata standar deviasi penjualan per periode adalah 10,29 .
Perhatikan bahwa deviasi standar rata-rata pada kedua contoh tersebut cukup mirip. Hal ini karena ukuran sampel (total transaksi) pada contoh kedua cukup dekat satu sama lain.
Kedua metode penghitungan deviasi standar rata-rata hanya berbeda secara signifikan ketika ukuran sampel berbeda secara signifikan antar kelompok.
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya