Deviasi standar sampel (atau deviasi standar sampel)
Artikel ini menjelaskan apa itu contoh deviasi standar dalam statistik. Demikian pula, Anda akan mempelajari cara menghitung simpangan baku sampel, latihan yang diselesaikan, dan apa perbedaan antara simpangan baku sampel dan simpangan baku populasi. Terakhir, Anda dapat menghitung deviasi standar sampel apa pun dengan kalkulator online.
Berapa simpangan baku sampelnya?
Simpangan baku sampel (atau simpangan baku sampel ) adalah ukuran penyebaran yang menunjukkan variabilitas suatu sampel. Lebih tepatnya, simpangan baku sampel sama dengan akar kuadrat dari jumlah kuadrat simpangan dibagi dengan ukuran sampel dikurangi satu.
Simbol simpangan baku sampel adalah huruf kecil s .
Deviasi standar sampel kadang-kadang disebut deviasi standar kuasi (atau deviasi standar kuasi) untuk membedakannya dari deviasi standar populasi. Di bawah ini kita akan melihat perbedaan simpangan baku sampel dengan simpangan baku populasi.
Contoh Rumus Deviasi Standar
Simpangan baku sampel sama dengan akar kuadrat dari jumlah kuadrat simpangan data sampel dibagi dengan ukuran sampel dikurangi satu. Oleh karena itu, rumus untuk menghitung simpangan baku sampel adalah:

Emas:
-

adalah simpangan baku sampel (atau simpangan baku sampel).
-

adalah nilai datanya

.
-

adalah ukuran sampel
-

adalah sarana sampel.
👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung deviasi standar sampel data apa pun.
Contoh penghitungan deviasi standar sampel
Sekarang setelah kita mengetahui definisi simpangan baku sampel (atau simpangan baku sampel) dan apa rumusnya, kita akan menyelesaikan contoh sederhana untuk menyelesaikan pemahaman cara menghitungnya.
- Sebuah perusahaan sepatu sedang melakukan riset pasar untuk memutuskan apakah akan meluncurkan model sepatu baru. Karena ada banyak model yang berbeda dan Anda hanya ingin melakukan analisis awal secara singkat, Anda memutuskan untuk melihat saja harga sampel dari lima merek sepatu pesaing teratas (harga ditunjukkan di bawah). Berapa simpangan baku kumpulan data ini?
€98 €70 €125 €89 €75
Untuk menghitung deviasi standar sampel, pertama-tama kita perlu menghitung mean sampel :
![]()
Setelah mean sampel dihitung, kami menerapkan rumus deviasi standar sampel:
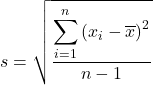
Kami mengganti data sampel ke dalam rumus:
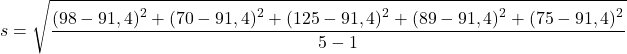
Jadi, yang tersisa hanyalah menyelesaikan operasi untuk menghitung deviasi standar sampel:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s&=\sqrt{\frac{6,6^2+(-21,4)^2+33,6^2+(-2,4)^2+(-16,4)^2}{4}}\\[2ex]\displaystyle s&=\sqrt{\frac{43,56+457,96+1128,96+5,76+268,96}{4}}\\[2ex]s&=\sqrt{\frac{1905,2}{4}}\\[2ex]s&=\sqrt{476,3}\\[2ex]s&=21,82 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0a9a5050ca14179085932bb9cc550ebb_l3.png)
Oleh karena itu, perbedaan pengambilan sampel dari sampel yang dianalisis adalah €21,82.
Simpangan baku sampel dan simpangan baku populasi
Selanjutnya, kita akan melihat perbedaan antara deviasi standar sampel dan deviasi standar populasi, karena ini adalah dua konsep statistik terkait yang perlu kita pahami dengan jelas.
Secara estadística, simpangan baku populasi adalah simpangan baku yang diperoleh jika melakukan perhitungan dengan seluruh elemen populasi, sedangkan simpangan baku adalah simpangan baku yang diperoleh dengan melakukan perhitungan hanya dengan satu contoh data dari populasi. .
Secara matematis, selisih simpangan baku sampel dan simpangan baku populasi merupakan penyebut rumus yang digunakan untuk menghitungnya. Untuk menghitung simpangan baku sampel harus dibagi n-1, sedangkan simpangan baku populasi dihitung dengan membagi n.
Selain itu, untuk membedakan simpangan baku sampel dari simpangan baku populasi, simpangan baku tersebut diwakili oleh simbol yang berbeda. Simbol simpangan baku sampel adalah huruf s, sedangkan lambang simpangan baku populasi adalah huruf Yunani σ.
Pada umumnya tidak semua unsur suatu populasi diketahui, oleh karena itu dilakukan studi statistik terhadap sampel populasi tersebut. Jadi, deviasi standar sampel digunakan untuk membuat perkiraan titik nilai deviasi standar seluruh populasi.
Contoh Kalkulator Deviasi Standar
Masukkan data sampel ke dalam kalkulator online berikut untuk menghitung deviasi standar sampel (atau deviasi standar sampel). Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.