Cara menghitung dfbetas di r

Dalam statistik, kita sering kali ingin mengetahui pengaruh observasi yang berbeda terhadap model regresi.

Salah satu cara untuk menghitung pengaruh observasi adalah dengan menggunakan metrik yang dikenal sebagai DFBETAS , yang memberi tahu kita efek standar pada setiap koefisien penghapusan setiap observasi individual.

Metrik ini memberi kita gambaran tentang pengaruh setiap observasi terhadap setiap estimasi koefisien dalam model regresi tertentu.

Tutorial ini menunjukkan contoh langkah demi langkah cara menghitung dan memvisualisasikan DFBETAS untuk setiap observasi dalam model di R.

Langkah 1: Buat model regresi

Pertama, kita akan membuat model regresi linier berganda menggunakan kumpulan data mtcars yang ada di R:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Langkah 2: Hitung DFBETAS untuk setiap observasi

Selanjutnya, kita akan menggunakan fungsi dfbetas() bawaan untuk menghitung nilai DFBETAS untuk setiap observasi dalam model:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Untuk setiap observasi, kita dapat melihat perbedaan estimasi koefisien titik asal, variabel disp , dan variabel hp yang muncul ketika kita menghapus observasi tersebut.

Secara umum, kami menganggap bahwa suatu observasi mempunyai pengaruh yang kuat terhadap estimasi koefisien tertentu jika observasi tersebut mempunyai nilai DBETAS yang lebih besar dari ambang batas 2/√ n dimana n adalah jumlah observasi.

Dalam contoh ini, ambang batasnya adalah 0.3535534 :

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Langkah 3: Visualisasikan DFBETAS

Terakhir, kita dapat membuat plot untuk memvisualisasikan nilai DFBETAS untuk setiap observasi dan setiap prediktor dalam model:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

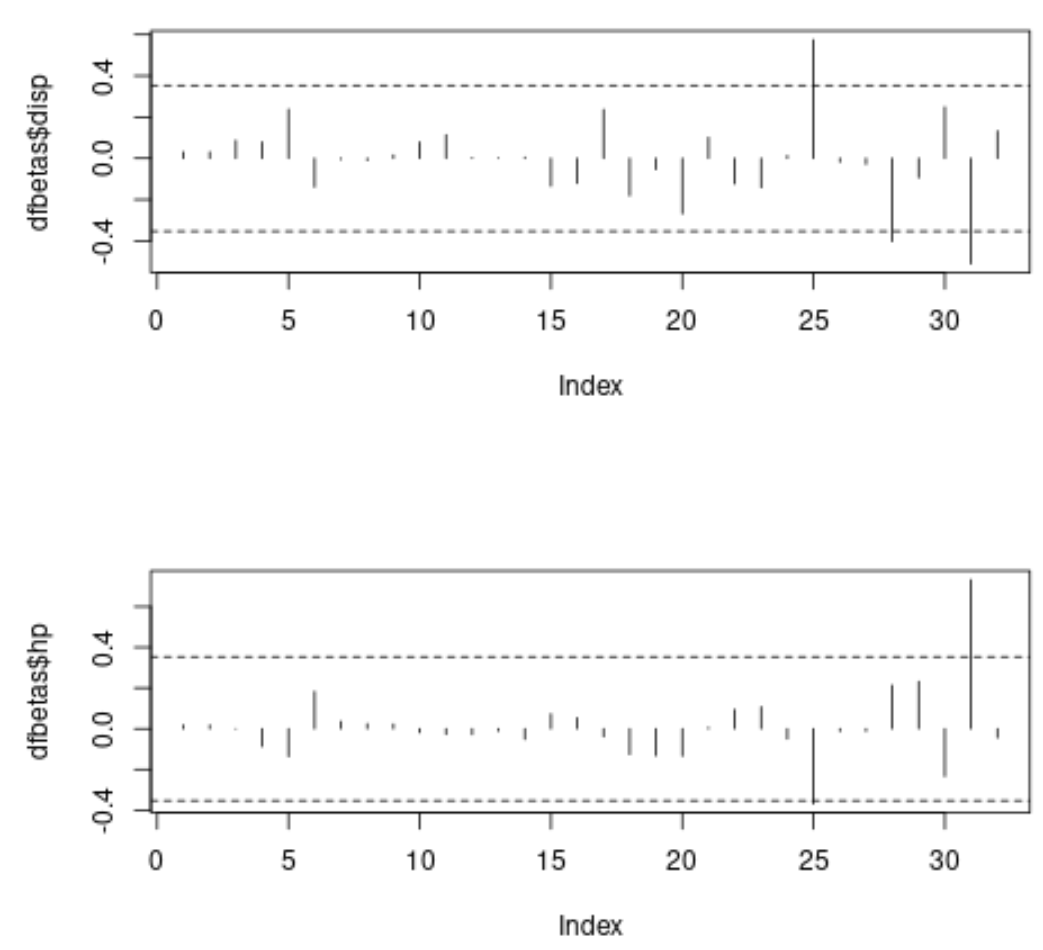
Di setiap plot, sumbu x menampilkan indeks setiap observasi dalam kumpulan data dan nilai y menampilkan DFBETAS yang sesuai untuk setiap observasi dan setiap prediktor.

Pada plot pertama terlihat tiga observasi melebihi nilai ambang batas absolut sebesar 0,3535534 dan pada plot kedua terlihat dua observasi melebihi nilai ambang batas absolut.

Kita dapat memilih untuk mempelajari observasi ini lebih dekat untuk menentukan apakah observasi tersebut mempunyai pengaruh yang tidak semestinya terhadap estimasi koefisien model.

Sumber daya tambahan

Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Cara menghitung statistik leverage di R
Cara menghitung DFFITS di R