Diagram pohon

Artikel ini menjelaskan apa itu diagram pohon dan cara pembuatannya. Jadi, Anda akan menemukan contoh struktur pohon, kelebihan diagram jenis ini, dan, sebagai tambahan, latihan yang diselesaikan langkah demi langkah.

Apa itu pohon?

Diagram pohon , juga disebut pohon probabilitas , adalah representasi grafis dari semua kemungkinan hasil percobaan beserta probabilitasnya.

Jadi, diagram pohon digunakan untuk membuat grafik semua kemungkinan hasil dalam ruang sampel dan menghitung probabilitasnya.

Diagram pohon dibuat sedemikian rupa sehingga setiap hasil ( node ) bercabang menjadi kemungkinan hasil baru ( cabang ) hingga tercapai hasil akhir.

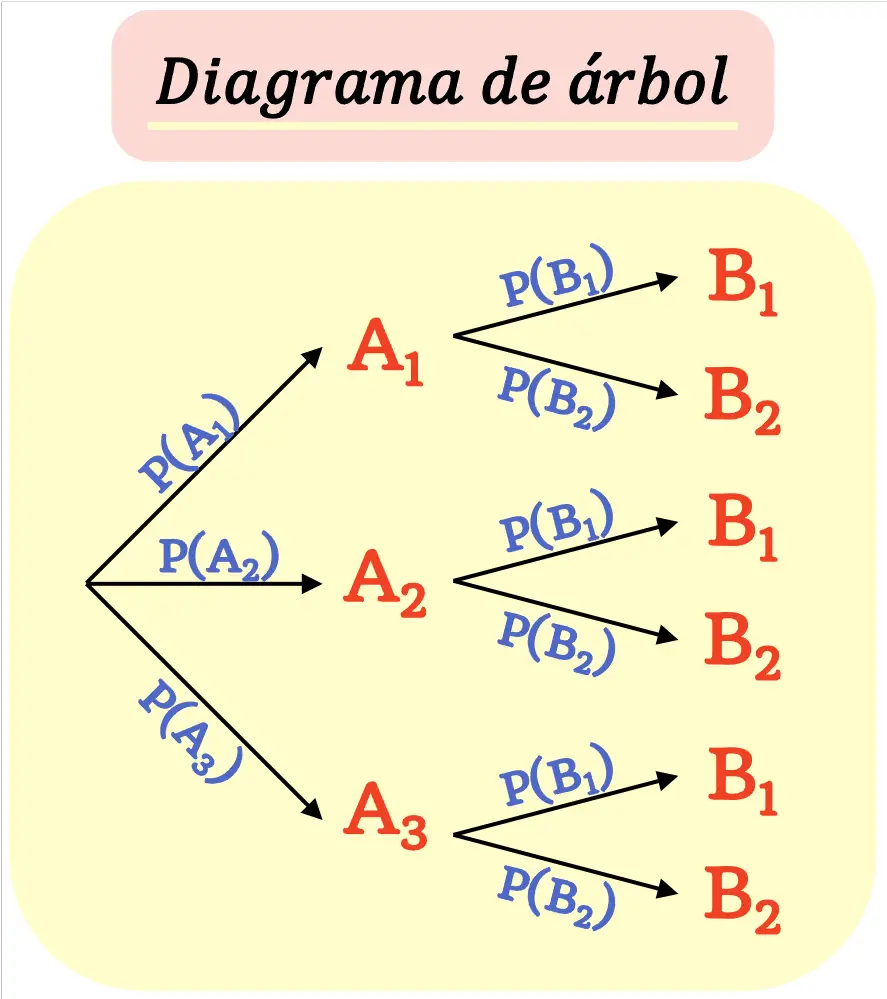
Perlu diingat bahwa jumlah probabilitas semua cabang yang keluar dari suatu node harus sama dengan 1.

Cara membuat diagram pohon

Untuk membuat pohon, Anda harus mengikuti langkah-langkah berikut:

1. Langkah pertama dalam membuat diagram pohon adalah menggambar cabang untuk setiap kemungkinan hasil. Ini akan menjadi cabang generasi pertama.
2. Kemudian, probabilitas yang terkait dengan setiap kejadian ditambahkan ke cabang terkaitnya.
3. Akhir dari setiap cabang generasi pertama adalah sebuah simpul dari mana cabang-cabang dari kejadian-kejadian berikutnya yang mungkin terjadi harus direpresentasikan.
4. Seperti pada cabang pertama, kita harus menjumlahkan probabilitas kejadian yang diwakili.
5. Ulangi langkah 3 dan 4 hingga Anda mencapai titik akhir, yaitu kemungkinan akhir percobaan.

Perhatikan bahwa jumlah cabang pada satu tingkat tidak harus sama dengan jumlah cabang pada tingkat yang berbeda. Demikian pula, jumlah cabang yang dihasilkan dari suatu kemungkinan dapat bervariasi bahkan dalam tingkat yang sama.

Contoh pohon

Sekarang setelah kita mengetahui definisi dan teori pembuatan diagram pohon, mari kita lihat contoh dunia nyata langkah demi langkah untuk lebih memahami konsep tersebut.

• Buatlah pohon probabilitas pelemparan koin dari tiga koin independen. Kemudian tentukan peluang munculnya kepala pada ketiga pelemparan tersebut.

Jika diundi, hanya ada dua kemungkinan hasil, kita bisa mendapatkan kepala atau ekor. Oleh karena itu, peluang munculnya kepala atau ekor pada pelemparan sebuah uang logam adalah:

Setelah kita mengetahui probabilitas hasil yang mungkin terjadi, kita lanjutkan dengan merepresentasikan diagram pohon.

Karena pelemparan koin bersifat independen, peluang munculnya kepala atau ekor akan selalu sama untuk setiap pelemparan. Oleh karena itu, untuk membangun pohon, dua cabang (kepala dan ekor) harus direpresentasikan dengan probabilitas yang sama untuk setiap lemparan yang dilakukan.

Dan setelah kita membuat pohonnya, yang harus kita lakukan hanyalah menentukan peluang terambilnya tiga buah koin.

Oleh karena itu, dalam hal ini kita harus mengalikan semua kemungkinan mendapatkan hasil, karena inilah kemungkinan jalan yang membawa kita ke hasil yang diinginkan.

Jadi, peluang munculnya gambar pada ketiga pelemparan koin dihitung sebagai berikut:

Singkatnya, kemungkinan mendapatkan gambar tiga kali berturut-turut adalah 12,5%.

Latihan pohon terpecahkan

Di sebuah desa hanya terdapat 3 panti asuhan: 60% anak bersekolah di panti A, 30% di panti B, dan 10% di panti C. Selain itu, di ketiga panti asuhan tersebut, 55% penduduknya adalah perempuan. Bangun pohonnya dan hitung probabilitas berikut:

• Peluang terambilnya seorang anak secara acak adalah anak perempuan dari tempat penitipan anak B.
• Kemungkinan ketika seorang anak dipilih secara acak dari pusat penitipan anak mana pun, ia akan berjenis kelamin laki-laki.

Perhatikan bahwa jika proporsi anak perempuan di semua tempat penitipan anak adalah 55%, maka persentase anak laki-laki dihitung hanya dengan mengurangkan 1 dikurangi 0,55:

Sekarang setelah kita mengetahui semua probabilitasnya, kita dapat membuat pohon probabilitas dengan semua kemungkinannya:

Jadi, peluang terpilihnya anak perempuan secara acak dari tempat penitipan anak B dihitung sebagai berikut:

Di sisi lain, untuk menentukan peluang terpilihnya anak laki-laki di tempat penitipan anak mana pun, pertama-tama kita harus mencari peluang terpilihnya anak laki-laki di setiap tempat penitipan anak, lalu menjumlahkannya:

Keuntungan dari struktur pohon

Karena sifat struktur pohonnya, kelebihan grafik statistik jenis ini adalah sebagai berikut:

• Diagram pohon sangat berguna untuk mengambil keputusan.
• Hubungan antara semua hasil yang mungkin dapat direpresentasikan secara grafis.
• Sangat mudah untuk menemukan akar penyebab suatu masalah.
• Memudahkan penyelesaian masalah probabilitas dan statistik.
• Diagram pohon membantu mengatur ide dan menganalisis situasi.