Distribusi binomial
Artikel ini menjelaskan apa itu distribusi binomial dalam statistik dan kegunaannya. Oleh karena itu, Anda akan menemukan definisi distribusi binomial, contoh distribusi binomial, dan sifat-sifat distribusi probabilitas jenis ini. Selain itu, Anda dapat menghitung probabilitas distribusi binomial dengan kalkulator online.
Apa yang dimaksud dengan distribusi binomial?
Distribusi binomial adalah distribusi probabilitas yang menghitung jumlah keberhasilan ketika melakukan serangkaian eksperimen independen dan dikotomis dengan probabilitas keberhasilan yang konstan.
Dengan kata lain, distribusi binomial adalah distribusi yang menggambarkan banyaknya hasil sukses dari suatu rangkaian percobaan Bernoulli.
Ingatlah bahwa uji Bernoulli adalah eksperimen yang mempunyai dua kemungkinan hasil: “berhasil” dan “gagal”. Oleh karena itu, jika peluang “berhasil” adalah p , peluang “gagal” adalah q=1-p .
Secara umum, jumlah percobaan yang dilakukan ditentukan dengan parameter n , sedangkan p adalah probabilitas keberhasilan setiap percobaan. Jadi, variabel acak yang mengikuti distribusi binomial ditulis sebagai berikut:
![]()
Perhatikan bahwa dalam distribusi binomial, percobaan yang sama persis diulang sebanyak n kali dan percobaan-percobaan tersebut independen satu sama lain, sehingga peluang keberhasilan setiap percobaan adalah sama (p) .
Distribusi binomial bisa juga disebut distribusi binomial .
Contoh Distribusi Binomial
Setelah kita melihat definisi distribusi binomial, kita akan melihat beberapa contoh variabel yang mengikuti jenis distribusi ini untuk lebih memahami konsepnya.
- Berapa kali muncul kepala pada pelemparan sebuah uang logam sebanyak 25 kali.
- Banyaknya tembakan yang dilakukan seorang pemain bola basket ketika ia menembak ke arah keranjang sebanyak 60 kali dari tempat yang sama.
- Berapa kali kita mendapatkan angka 6 dengan cara melempar sebuah dadu sebanyak 30 kali.
- Jumlah kelulusan dari total 50 siswa yang mengikuti ujian.
- Jumlah unit cacat dalam sampel 100 produk.
Rumus distribusi binomial
Mengingat parameter x, n, p, fungsi probabilitas dari distribusi binomial didefinisikan sebagai bilangan kombinatorial n dalam x kali p x kali (1-p) nx .
Oleh karena itu, rumus menghitung peluang distribusi binomial adalah:

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung peluang suatu variabel yang mengikuti distribusi binomial.
Sebaliknya, probabilitas kumulatif dari distribusi binomial dihitung dengan menjumlahkan probabilitas jumlah kasus keberhasilan yang bersangkutan dan seluruh probabilitas sebelumnya. Jadi, rumus menghitung probabilitas kumulatif dari distribusi binomial adalah:
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e31ef4ae023b8bf51c0b6816bc787c91_l3.png)
Latihan soal distribusi binomial
- Sebuah koin dilempar sebanyak 10 kali, berapa peluang terambilnya 6 gambar?
Variabel dalam soal ini mengikuti distribusi binomial karena semua peluncuran tidak bergantung satu sama lain dan juga memiliki peluang keberhasilan yang sama.
Konkretnya, probabilitas suksesnya adalah 50%, karena hanya satu dari dua kemungkinan hasil yang dianggap sukses.
![]()
Oleh karena itu, distribusi latihan ini adalah binomial dengan total 10 percobaan dan probabilitas 0,5.
![]()
Jadi, untuk menentukan peluang terambilnya enam gambar, kita perlu menerapkan rumus distribusi binomial.
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-17346d59c641378880b734dfe88210f6_l3.png)
Jadi, peluang terambilnya tepat enam gambar dengan pelemparan sebuah uang logam sebanyak sepuluh kali adalah 20,51%.
Ciri-ciri distribusi binomial
Distribusi binomial mempunyai ciri-ciri sebagai berikut:
- Distribusi binomial ditentukan dengan dua parameter: n adalah jumlah total percobaan Bernoulli dan, sebaliknya, p adalah probabilitas keberhasilan setiap percobaan Bernoulli.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cd9728a237a5f49107bf14f440620936_l3.png)
- Rata-rata distribusi binomial sama dengan hasil kali jumlah percobaan dikalikan dengan peluang keberhasilan setiap percobaan. Oleh karena itu, untuk menghitung rata-rata distribusi binomial, kita harus mengalikan n dengan p .
![]()
- Varians distribusi binomial sama dengan jumlah percobaan dikalikan dengan probabilitas keberhasilan dan probabilitas kegagalan.
![]()
- Rumus fungsi probabilitas dari distribusi binomial adalah sebagai berikut:
![]()
- Demikian pula rumus fungsi distribusi kumulatif dari distribusi binomial adalah:
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e31ef4ae023b8bf51c0b6816bc787c91_l3.png)
- Jumlah dua distribusi binomial bebas yang mempunyai peluang yang sama ekuivalen dengan suatu distribusi binomial yang nilai peluangnya sama p dan n merupakan jumlah dari jumlah percobaan kedua distribusi tersebut.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dbc1a01b2d5654864d688cc46ac3a2e6_l3.png)
![]()
- Distribusi Bernoulli merupakan kasus khusus dari distribusi binomial dimana n=1 , yaitu hanya satu percobaan yang dilakukan.
![]()
- Jika X 1 , X 2 ,…, X k adalah peubah acak bebas sedemikian rupa sehingga
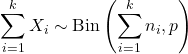
Kalkulator Distribusi Binomial
Masukkan nilai parameter p, n dan x dari distribusi binomial ke dalam kalkulator berikut untuk menghitung probabilitas. Anda perlu memilih probabilitas yang ingin Anda hitung dan memasukkan angka menggunakan titik sebagai pemisah desimal, misalnya 0,1667.