Distribusi binomial negatif

Oleh Benjamin anderson Agustus 3, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu distribusi binomial negatif dan kegunaannya. Anda juga akan menemukan rumus distribusi binomial negatif, contoh nyata dan sifat-sifat distribusi probabilitas jenis ini. Terakhir, Anda dapat menghitung probabilitas distribusi binomial negatif dengan kalkulator online.

Berapakah distribusi binomial negatif?

Distribusi binomial negatif adalah distribusi probabilitas yang menggambarkan jumlah percobaan Bernoulli yang diperlukan untuk memperoleh sejumlah hasil positif.

Oleh karena itu, distribusi binomial negatif memiliki dua parameter karakteristik: r adalah jumlah hasil sukses yang diinginkan dan p adalah probabilitas keberhasilan setiap percobaan Bernoulli yang dilakukan.

$X\sim \text{BN}(r,p)$

Ingatlah bahwa uji Bernoulli adalah eksperimen yang mempunyai dua kemungkinan hasil: “berhasil” dan “gagal”. Jadi jika peluang “berhasil” adalah p , peluang “gagal” adalah q=1-p .

Jadi, distribusi binomial negatif mendefinisikan suatu proses di mana percobaan Bernoulli dilakukan sebanyak yang diperlukan untuk mendapatkan hasil yang positif. Selain itu, semua uji coba Bernoulli ini bersifat independen dan memiliki kemungkinan keberhasilan yang konstan.

Misalnya, variabel acak yang mengikuti distribusi binomial negatif adalah berapa kali sebuah dadu harus dilempar hingga angka 6 dilempar tiga kali.

Perbedaan antara distribusi binomial negatif dan distribusi binomial adalah distribusi binomial negatif menghitung berapa kali yang diperlukan untuk mendapatkan sejumlah hasil yang berhasil, sedangkan distribusi binomial menghitung jumlah kasus yang berhasil dalam serangkaian uji Bernoulli.

➤ Lihat: Apa yang dimaksud dengan distribusi binomial?

Rumus distribusi binomial negatif

Mengingat parameter r, p, x, probabilitas distribusi binomial negatif dihitung dengan mengalikan bilangan kombinatorial x-1 dalam xr dengan (1-p) ^xr dengan p ^r .

Jadi, rumus menghitung probabilitas distribusi binomial negatif adalah:

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung peluang suatu variabel yang mengikuti distribusi binomial negatif.

Latihan terpecahkan dari distribusi binomial negatif

Berapa peluang sebuah mata uang dilempar delapan kali dan muncul gambar keempat kalinya pada pelemparan kedelapan?

Pertama, kita perlu menghitung peluang munculnya kepala saat melempar koin. Dalam hal ini, kita hanya mempunyai satu hasil positif (head) dari dua kemungkinan hasil (head dan tail), sehingga peluang suksesnya adalah:

$p=\cfrac{1}{2}=0,5$

Jadi, variabel acak dalam soal ini mengikuti distribusi binomial negatif di mana r=4 dan p=0,5. Oleh karena itu, kami menggunakan rumus distribusi binomial negatif untuk menghitung probabilitas yang diminta oleh latihan tersebut.

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

Ciri-ciri distribusi binomial negatif

Di bawah ini adalah ciri-ciri terpenting dari distribusi binomial negatif.

Distribusi binomial negatif ditentukan oleh dua parameter karakteristik: r adalah jumlah hasil sukses yang diinginkan dan p adalah probabilitas keberhasilan setiap percobaan Bernoulli yang dilakukan.

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

Varians dari distribusi binomial negatif sama dengan r dikalikan (1-p) dibagi p ² .

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

Jika parameter r lebih besar dari 1, modus distribusi binomial negatif dapat dihitung dengan rumus berikut:

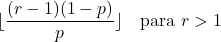
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”221″ style=”vertical-align: -16px;”></p> </p> <ul> <li> Fungsi massa yang memungkinkan untuk menentukan probabilitas distribusi binomial negatif adalah sebagai berikut:</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

Koefisien skewness dari distribusi binomial negatif dihitung dengan ekspresi berikut:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

Kurtosis distribusi binomial negatif dapat dicari dengan rumus berikut:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

Jika parameter r sama dengan 1, maka kita mempunyai kasus distribusi geometri .

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

Kalkulator Distribusi Binomial Negatif

Masukkan nilai parameter r, p, x ke dalam kalkulator berikut untuk menghitung probabilitas. Anda harus memasukkan angka menggunakan titik sebagai pemisah desimal, misalnya 0,50.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya