Distribusi chi-kuadrat

Oleh Benjamin anderson Agustus 4, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu distribusi chi-kuadrat dan kegunaannya. Selain itu, Anda akan menemukan grafik distribusi chi-kuadrat dan propertinya.

Berapakah distribusi chi-kuadratnya?

Distribusi Chi-kuadrat merupakan distribusi probabilitas yang simbolnya adalah χ². Lebih tepatnya, distribusi Chi-kuadrat adalah jumlah kuadrat dari k variabel acak independen yang berdistribusi normal.

Jadi, distribusi Chi-kuadrat mempunyai k derajat kebebasan. Oleh karena itu, distribusi Chi-kuadrat mempunyai derajat kebebasan yang sama dengan jumlah kuadrat dari variabel-variabel berdistribusi normal yang diwakilinya.

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

Distribusi Chi-kuadrat juga dikenal sebagai distribusi Pearson .

Perlu dicatat bahwa distribusi Chi-kuadrat adalah kasus khusus dari distribusi gamma.

Distribusi chi-kuadrat banyak digunakan dalam inferensi statistik, misalnya dalam pengujian hipotesis dan interval kepercayaan. Kita akan melihat di bawah apa saja penerapan jenis distribusi probabilitas ini.

Grafik distribusi chi-kuadrat

Setelah kita melihat definisi distribusi Chi-kuadrat, kita akan melihat beberapa contoh distribusi jenis ini yang direpresentasikan secara grafis. Jadi di bawah ini Anda dapat melihat bagaimana plot probabilitas distribusi chi-kuadrat bervariasi bergantung pada derajat kebebasan.

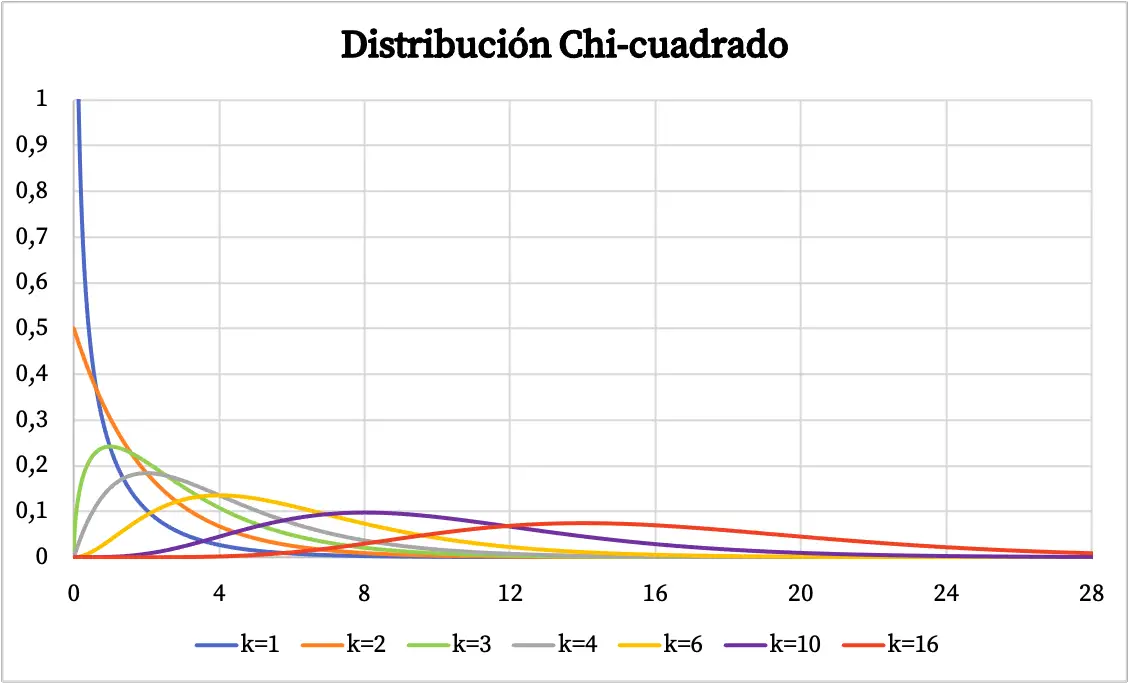
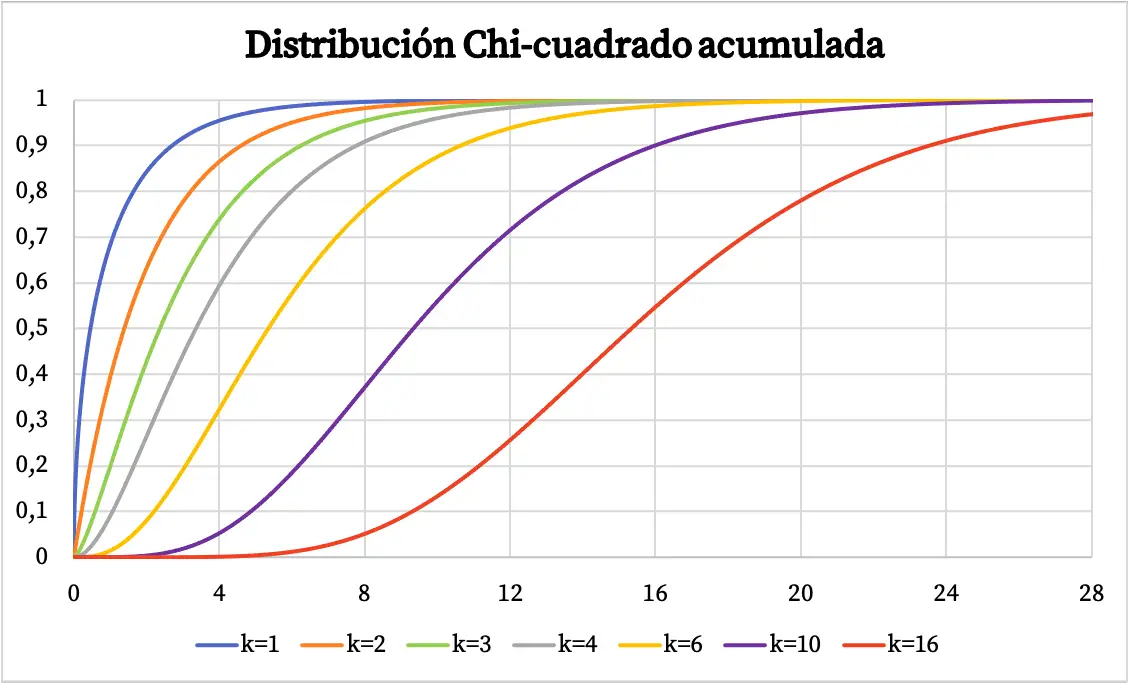
Fungsi kepadatan distribusi Chi-kuadrat telah digambarkan pada grafik di atas. Sedangkan grafik fungsi distribusi probabilitas kumulatif chi-kuadrat adalah sebagai berikut:

➤ Lihat: Tabel distribusi chi-kuadrat

Karakteristik distribusi chi-kuadrat

Pada bagian ini kita akan melihat sifat terpenting dari distribusi Chi-kuadrat yang berkaitan dengan teori probabilitas dan statistik.

Rata-rata distribusi chi-kuadrat sama dengan derajat kebebasannya.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

Varians suatu distribusi Chi-kuadrat sama dengan dua kali derajat kebebasan distribusi.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

Modus distribusi chi-kuadrat adalah dua satuan lebih kecil dari derajat kebebasannya, selama distribusi tersebut mempunyai lebih dari satu derajat kebebasan.

$Mo=k-2 \qquad \text{si } k\geq 2$

Fungsi kepadatan distribusi Chi-kuadrat adalah nol jika x=0. Namun, untuk nilai x lebih besar dari 0, fungsi kepadatan distribusi Chi-kuadrat ditentukan dengan rumus berikut:

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

Fungsi distribusi kumulatif dari distribusi Chi-kuadrat diatur dengan rumus berikut:

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

Koefisien skewness distribusi Chi-kuadrat adalah akar kuadrat dari hasil bagi delapan dibagi jumlah derajat kebebasan distribusi.

$\displaystyle A=\sqrt{\frac{8}{k}}$

Kurtosis distribusi Chi-kuadrat dihitung menggunakan persamaan berikut:

$C=3+\cfrac{12}{k}$

Karena teorema limit pusat, distribusi chi-kuadrat dapat didekati dengan distribusi normal jika k cukup besar.

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

Penerapan distribusi chi-kuadrat

Distribusi chi-kuadrat memiliki banyak penerapan berbeda dalam statistik. Faktanya, terdapat uji chi-square yang digunakan untuk memeriksa independensi antar variabel dan kesesuaian dengan distribusi teoritis. Misalnya, uji Chi-kuadrat dapat digunakan untuk menentukan apakah data sampel sesuai dengan distribusi Poisson.

Dalam analisis regresi linier, distribusi chi-kuadrat juga digunakan untuk memperkirakan rata-rata populasi yang berdistribusi normal dan memperkirakan kemiringan garis studi regresi linier.

Terakhir, distribusi Chi kuadrat juga ikut serta dalam analisis varians, melalui hubungannya dengan distribusi Snedecor F.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya