Distribusi snedecor f

Oleh Agustus 4, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu distribusi Snedecor F dan kegunaannya. Selain itu, Anda akan dapat melihat grafik distribusi Snedecor F dan sifat statistiknya.

Apa distribusi Snedecor F?

Distribusi Snedecor F , juga disebut distribusi Fisher – Snedecor F atau sederhananya distribusi F , adalah distribusi probabilitas kontinu yang digunakan dalam inferensi statistik, khususnya dalam analisis varians.

Salah satu sifat distribusi Snedecor F adalah distribusi tersebut ditentukan oleh nilai dua parameter nyata, m dan n , yang menunjukkan derajat kebebasannya. Jadi, simbol distribusi Snedecor F adalah F m,n , dengan m dan n adalah parameter yang menentukan distribusi tersebut.

F_{m,n}\qquad m,n>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”139″ style=”vertical-align: -6px;”></p> </p> <p> Secara matematis, distribusi Snedecor F sama dengan hasil bagi antara suatu distribusi chi-kuadrat dan derajat kebebasannya dibagi dengan hasil bagi antara distribusi chi-kuadrat yang lain dan derajat kebebasannya. Jadi rumus yang mendefinisikan distribusi Snedecor F adalah sebagai berikut: </p> </p> <p class=\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}

Distribusi Fisher-Snedecor F mendapatkan namanya dari ahli statistik Inggris Ronald Fisher dan ahli statistik Amerika George Snedecor.

Dalam statistik, distribusi Fisher-Snedecor F memiliki penerapan berbeda. Misalnya, distribusi Fisher-Snedecor F digunakan untuk membandingkan model regresi linier yang berbeda, dan distribusi probabilitas ini digunakan dalam analisis varians (ANOVA).

Diagram distribusi Snedecor F

Setelah kita melihat definisi distribusi Snedecor F, grafik fungsi kepadatannya dan grafik probabilitas kumulatifnya ditunjukkan di bawah ini.

Pada grafik di bawah ini Anda dapat melihat beberapa contoh distribusi Snedecor F dengan derajat kebebasan yang berbeda-beda.

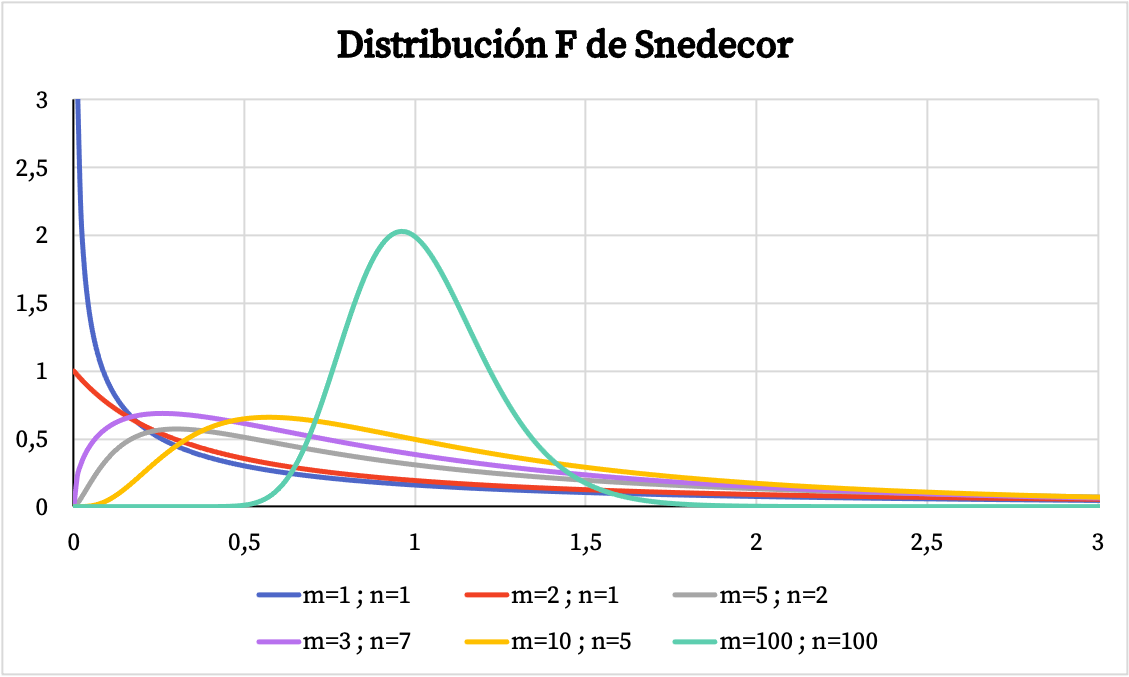
Grafik distribusi Snedecor F

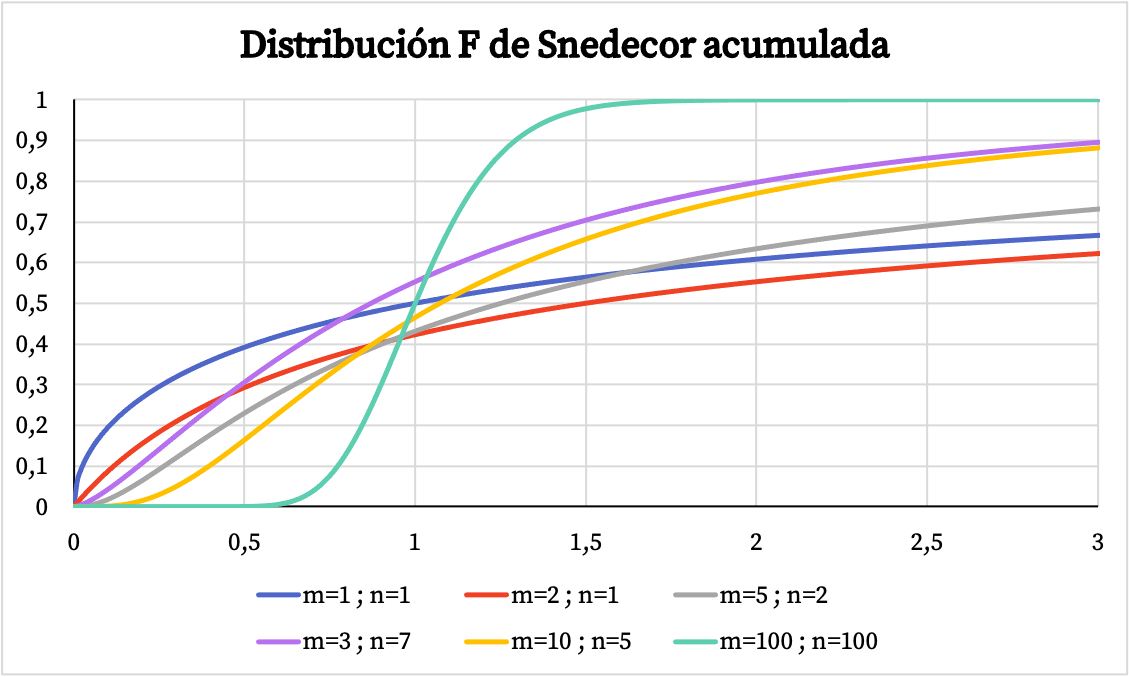
Sebaliknya, pada grafik di bawah ini Anda dapat melihat bagaimana grafik fungsi probabilitas kumulatif dari distribusi Snedecor F bervariasi bergantung pada nilai karakteristiknya.

probabilitas kumulatif dari distribusi Snedecor F

Karakteristik distribusi Snedecor F

Terakhir, bagian ini menyajikan karakteristik terpenting dari distribusi Snedecor F.

  • Derajat kebebasan distribusi Snedecor F, m dan n , adalah dua parameter yang menentukan bentuk distribusi. Nilai karakteristik distribusi Snedecor F ini adalah bilangan bulat positif.

\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Domain distribusi Snedecor F terdiri dari semua bilangan real yang lebih besar atau sama dengan nol.</li> </ul> <p class=x\in [0,+\infty)

  • Untuk nilai n lebih besar dari 2, mean distribusi Snedecor F sama dengan n pada pengurangan n dikurangi 2.

\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Jika parameter <em>n</em> lebih besar dari 2, varians distribusi Snedecor F dapat dihitung dengan menggunakan rumus berikut:</li> </ul> <p class=\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Jika parameter <em>m</em> lebih besar dari 2, modus distribusi Snedecor F dapat dihitung dengan ekspresi berikut:</li> </ul> <p class=Mo=\cfrac{m-2}{m}\cdot \cfrac{n}{n+2}\qquad \text{para }m>2″ title=”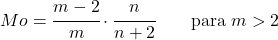Rendered by QuickLaTeX.com” height=”40″ width=”278″ style=”vertical-align: -14px;”></p> </p> <ul> <li> Rumus fungsi densitas distribusi Snedecor F adalah sebagai berikut:</li> </ul> <p class=\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}

  • Jika suatu variabel mengikuti distribusi Snedecor F dengan derajat kebebasan m dan n , maka kebalikan dari variabel tersebut mengikuti distribusi Snedecor F dengan derajat kebebasan yang sama tetapi urutan nilainya berubah.

X\sim F_{m,n} \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^{-1}\sim F_{n,m}

  • Distribusi Student mempunyai hubungan sebagai berikut dengan distribusi Snedecor F:

X\sim t_n \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^2\sim F_{1,n}

Tentang Penulis

Benjamin Anderson
Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Tambahkan komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *