Pengenalan distribusi poisson

Distribusi Poisson adalah salah satu distribusi yang paling populer dalam statistik.

Untuk memahami distribusi Poisson, ada gunanya memahami eksperimen Poisson terlebih dahulu.

Eksperimen Ikan

Eksperimen Poisson adalah eksperimen yang mempunyai sifat-sifat sebagai berikut:

• Jumlah keberhasilan percobaan dapat dihitung.
• Jumlah rata-rata keberhasilan yang terjadi selama interval waktu (atau ruang) tertentu diketahui.
• Setiap hasil bersifat independen.
• Peluang suksesnya kejadian sebanding dengan besarnya interval.

Contoh percobaan Poisson adalah jumlah kelahiran per jam di suatu rumah sakit. Misalnya, sebuah rumah sakit tertentu rata-rata menerima 10 kelahiran per jam. Ini adalah eksperimen Poisson karena mempunyai empat sifat berikut:

• Jumlah keberhasilan percobaan dapat dihitung – Kita dapat menghitung jumlah kelahiran.
• Diketahui rata-rata jumlah kelahiran yang terjadi dalam selang waktu tertentu – Diketahui rata-rata 10 kelahiran per jam.
• Setiap hasil bersifat independen – Probabilitas seorang ibu akan melahirkan pada jam tertentu tidak tergantung pada probabilitas ibu lain akan melahirkan.
• Kemungkinan terjadinya keberhasilan sebanding dengan besarnya interval: semakin panjang interval waktu, semakin tinggi kemungkinan terjadinya kelahiran.

Distribusi Poisson dapat kita gunakan untuk menjawab pertanyaan tentang probabilitas percobaan Poisson ini seperti:

• Berapa peluang terjadinya lebih dari 12 kelahiran dalam satu jam tertentu?
• Berapa peluang terjadinya kurang dari 5 kelahiran dalam satu jam tertentu?
• Berapa peluang terjadinya antara 8 dan 11 kelahiran pada jam tertentu?

Distribusi Ikan

Distribusi Poisson menggambarkan probabilitas diperolehnya k keberhasilan selama selang waktu tertentu.

Jika suatu variabel acak X mengikuti distribusi Poisson, maka peluang keberhasilan X = k dapat dicari dengan rumus berikut:

P(X=k) = λ ^k * e ^{– λ} / k!

Emas:

• λ: jumlah rata-rata keberhasilan yang terjadi selama interval tertentu
• k: jumlah keberhasilan
• e: konstanta sama dengan sekitar 2,71828

Misalnya, sebuah rumah sakit tertentu mengalami rata-rata 2 kelahiran per jam. Kita dapat menggunakan rumus di atas untuk menentukan peluang mengalami kelahiran 0, 1, 2, 3, dst. dalam satu jam tertentu:

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707

P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Kita dapat menghitung probabilitas sejumlah kelahiran hingga tak terhingga. Kami kemudian membuat histogram sederhana untuk memvisualisasikan distribusi probabilitas ini:

Perhitungan probabilitas Poisson kumulatif

Menghitung probabilitas Poisson tunggal (misalnya probabilitas sebuah rumah sakit mengalami 3 kelahiran dalam satu jam tertentu) dapat dilakukan dengan mudah menggunakan rumus di atas, namun untuk menghitung probabilitas Poisson kumulatif kita perlu menambahkan probabilitas individual.

Misalnya, kita ingin mengetahui probabilitas suatu rumah sakit akan mengalami 1 kelahiran atau kurang dalam satu jam tertentu. Kami akan menggunakan rumus berikut untuk menghitung probabilitas ini:

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

Ini disebut probabilitas kumulatif karena melibatkan penambahan beberapa probabilitas. Kita dapat menghitung probabilitas kumulatif untuk mengalami k atau lebih sedikit kelahiran dalam satu jam tertentu dengan menggunakan rumus serupa:

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

Kita dapat menghitung probabilitas kumulatif ini untuk sejumlah kelahiran hingga tak terhingga. Kita kemudian dapat membuat histogram untuk memvisualisasikan distribusi probabilitas kumulatif ini:

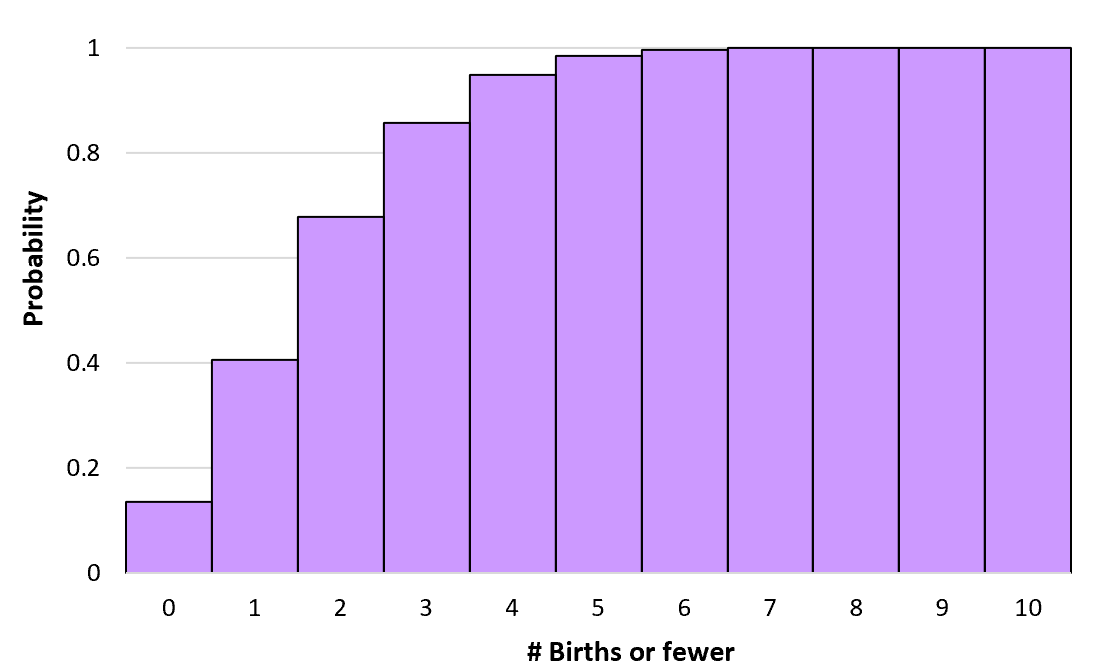
Sifat-sifat distribusi Poisson

Distribusi Poisson mempunyai sifat sebagai berikut:

Rata-rata distribusinya adalah λ .

Varians distribusinya juga λ .

Simpangan baku distribusinya adalah √ λ .

Misalnya, sebuah rumah sakit rata-rata menerima 2 kelahiran per jam.

Rata-rata jumlah kelahiran yang diharapkan dalam satu jam tertentu adalah λ = 2 kelahiran.

Varians jumlah kelahiran yang kita harapkan adalah λ = 2 kelahiran.

Soal praktek distribusi ikan

Gunakan soal latihan berikut untuk menguji pengetahuan Anda tentang distribusi Poisson.

Catatan: Kami akan menggunakan kalkulator distribusi Poisson untuk menghitung jawaban atas pertanyaan-pertanyaan ini.

Masalah 1

Pertanyaan: Kita tahu bahwa situs web tertentu menghasilkan 10 penjualan per jam. Dalam satu jam tertentu, berapa peluang situs tersebut menghasilkan tepat 8 penjualan?

Jawaban: Dengan menggunakan kalkulator distribusi Poisson dengan λ = 10 dan x = 8, diperoleh P(X=8) = 0,1126 .

Masalah 2

Pertanyaan: Kita tahu bahwa seorang agen real estat tertentu menghasilkan rata-rata 5 penjualan per bulan. Pada bulan tertentu, berapa peluang dia menghasilkan lebih dari 7 penjualan?

Jawaban: Dengan menggunakan kalkulator distribusi Poisson dengan λ = 5 dan x = 7, diperoleh P(X>7) = 0,13337 .

Masalah 3

Pertanyaan: Kita tahu bahwa suatu rumah sakit tertentu mengalami 4 kali persalinan per jam. Dalam satu jam tertentu, berapa peluang terjadinya 4 kelahiran atau kurang?

Jawaban: Dengan menggunakan kalkulator distribusi Poisson dengan λ = 4 dan x = 4, diperoleh P(X≤4) = 0,62884 .

Sumber daya tambahan

Artikel berikut menjelaskan cara menggunakan distribusi Poisson di berbagai perangkat lunak statistik:

Cara menggunakan distribusi Poisson di R
Cara menggunakan distribusi Poisson di Excel
Cara Menghitung Probabilitas Poisson pada Kalkulator TI-84
Contoh distribusi Poisson di dunia nyata
Kalkulator Distribusi Ikan