Distribusi normal

Distribusi normal adalah distribusi probabilitas yang paling umum dalam statistik.

Distribusi normal mempunyai ciri-ciri sebagai berikut:

• Bentuk lonceng
• Simetris
• Rata-rata dan mediannya sama; keduanya terletak di pusat distribusi
• Sekitar 68% data berada dalam satu standar deviasi mean
• Sekitar 95% data berada dalam dua standar deviasi dari mean.
• Sekitar 99,7% data berada dalam tiga standar deviasi mean.

Tiga poin terakhir dikenal sebagai aturan praktis , terkadang disebut aturan 68-95-99.7 .

Terkait: Rule of Thumb (Masalah Latihan)

Cara menggambar kurva normal

Untuk menggambar kurva normal, kita perlu mengetahui mean dan deviasi standarnya.

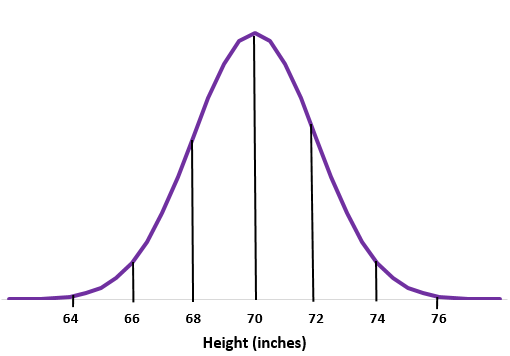
Contoh 1: Misalkan tinggi badan laki-laki di suatu sekolah berdistribusi normal dengan rata-rata $\mu =\; 70\; inci\; dan$ simpangan baku $\sigma \; =\; 2\; inci.\; Buat\; sketsa\; kurva\; normal.$

Langkah 1: Buat sketsa kurva normal.

Langkah 2: Rata-rata 70 inci berada di tengah.

Langkah 3: Setiap deviasi standar berhubungan dengan jarak 2 inci.

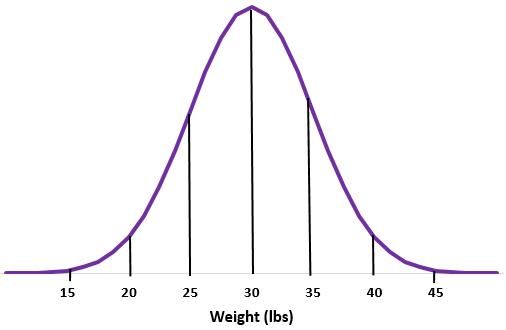
Contoh 2: Misalkan berat spesies berang-berang tertentu berdistribusi normal dengan rata-rata $\mu =\; 30\; pon\; dan$ simpangan baku $\sigma \; =\; 5\; pon.\; Buat\; sketsa\; kurva\; normal.$

Langkah 1: Buat sketsa kurva normal.

Langkah 2: Rata-rata 30 pon berada di tengah.

Langkah 3: Setiap deviasi standar setara dengan jarak 5 lbs

Cara Mencari Persentase Menggunakan Distribusi Normal

Aturan praktisnya , terkadang disebut aturan 68-95-99.7 , menyatakan bahwa untuk variabel acak yang berdistribusi normal, 68% data berada dalam rentang satu deviasi standar dari rata-rata, 95% berada dalam rentang dua deviasi standar. deviasi dari mean dan 99,7% berada dalam tiga standar deviasi dari mean.

Dengan menggunakan aturan ini kita dapat menjawab pertanyaan tentang persentase.

Contoh: Misalkan tinggi badan laki-laki di suatu sekolah berdistribusi normal dengan rata-rata $\mu =\; 70\; inci\; dan$ simpangan baku $\sigma \; =\; 2\; inci.$

$Kira-kira\; berapa\; persentase\; pria\; di\; sekolah\; ini\; yang\; tingginya\; lebih\; dari\; 74\; inci?$

Larutan:

Langkah 1: Buat sketsa distribusi normal dengan rata-rata $\mu =\; 70\; inci\; dan$ simpangan baku $\sigma \; =\; 2\; inci.$

Langkah 2: Tinggi 74 inci adalah dua standar deviasi di atas rata-rata. Tambahkan persentase di atas titik ini ke dalam distribusi normal.

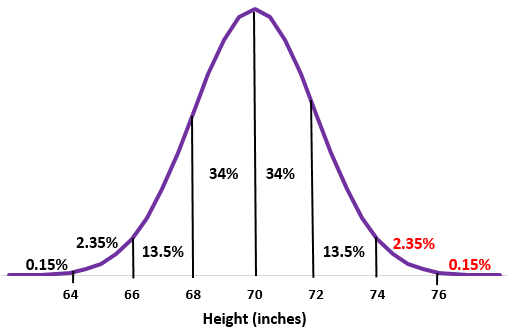
2,35% + 0,15% = 2,5%

Sekitar 2,5% pria di sekolah ini memiliki tinggi lebih dari 74 inci.

$Kira-kira\; berapa\; persentase\; pria\; di\; sekolah\; ini\; yang\; tingginya\; antara\; 68\; inci\; dan\; 72\; inci?$

Larutan:

Langkah 1: Buat sketsa distribusi normal dengan rata-rata $\mu =\; 70\; inci\; dan$ simpangan baku $\sigma \; =\; 2\; inci.$

Langkah 2: Tinggi badan 68 inci dan 72 inci masing-masing merupakan satu standar deviasi di bawah dan di atas rata-rata. Cukup tambahkan persentase antara dua titik ini dalam distribusi normal.

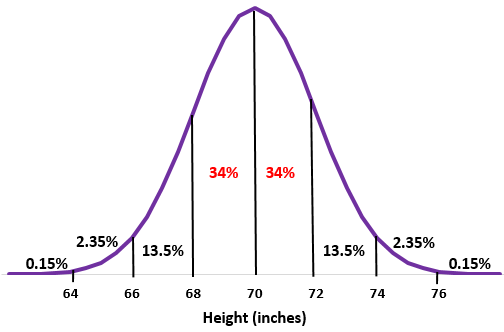
34% + 34% = 68%

Sekitar 68% pria di sekolah ini memiliki tinggi antara 68 inci dan 72 inci.

Cara mencari hitungan menggunakan distribusi normal

Kita juga bisa menggunakan aturan praktis untuk menjawab pertanyaan tentang hitungan.

Contoh: Misalkan berat suatu spesies berang-berang tertentu berdistribusi normal dengan rata-rata $\mu =\; 30\; pon\; dan$ simpangan baku $\sigma \; =\; 5\; pon.$

Sebuah koloni tertentu memiliki 200 ekor berang-berang ini. Kira-kira berapa banyak berang-berang yang beratnya lebih dari 35 pon?

Larutan:

Langkah 1: Buat sketsa distribusi normal dengan rata-rata $\mu =\; 30\; lb\; dan$ simpangan baku $\sigma \; =\; 5\; lb.$

Langkah 2: Berat 35 pon adalah satu standar deviasi di atas rata-rata. Tambahkan persentase di atas titik ini ke dalam distribusi normal.

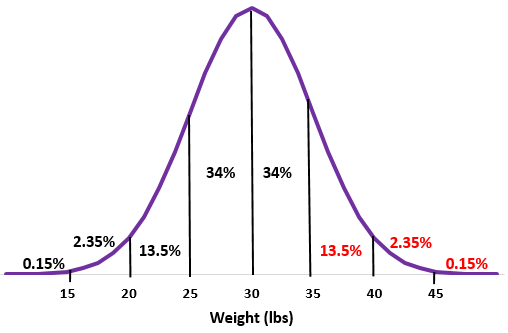
13,5% + 2,35% + 0,15% = 16%

Langkah 3: Karena ada 200 berang-berang di koloni, 16% dari 200 = 0,16 * 200 = 32

Sekitar 32 berang-berang di koloni ini memiliki berat lebih dari 35 pon.

Kira-kira berapa banyak berang-berang di koloni ini yang beratnya kurang dari 30 pon?

Daripada mengikuti semua langkah yang baru saja kita ambil di atas, kita dapat mengetahui bahwa median dari distribusi normal sama dengan mean, yaitu dalam kasus ini adalah 30 pon.

Ini berarti setengah dari berang-berang memiliki berat lebih dari 30 pon dan separuh lainnya memiliki berat kurang dari 30 pon. Artinya 50% dari 200 berang-berang memiliki berat kurang dari 30 pon, jadi 0,5 * 200 = 100 berang-berang .

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang distribusi normal:

6 contoh konkrit distribusi normal
Distribusi normal vs distribusi t: perbedaannya
Cara Membuat Kurva Lonceng di Excel
Cara Membuat Kurva Lonceng dengan Python