Distribusi normal dan distribusi t: apa bedanya?

Distribusi normal adalah distribusi yang paling umum digunakan dalam semua statistik dan dikenal simetris dan berbentuk lonceng.

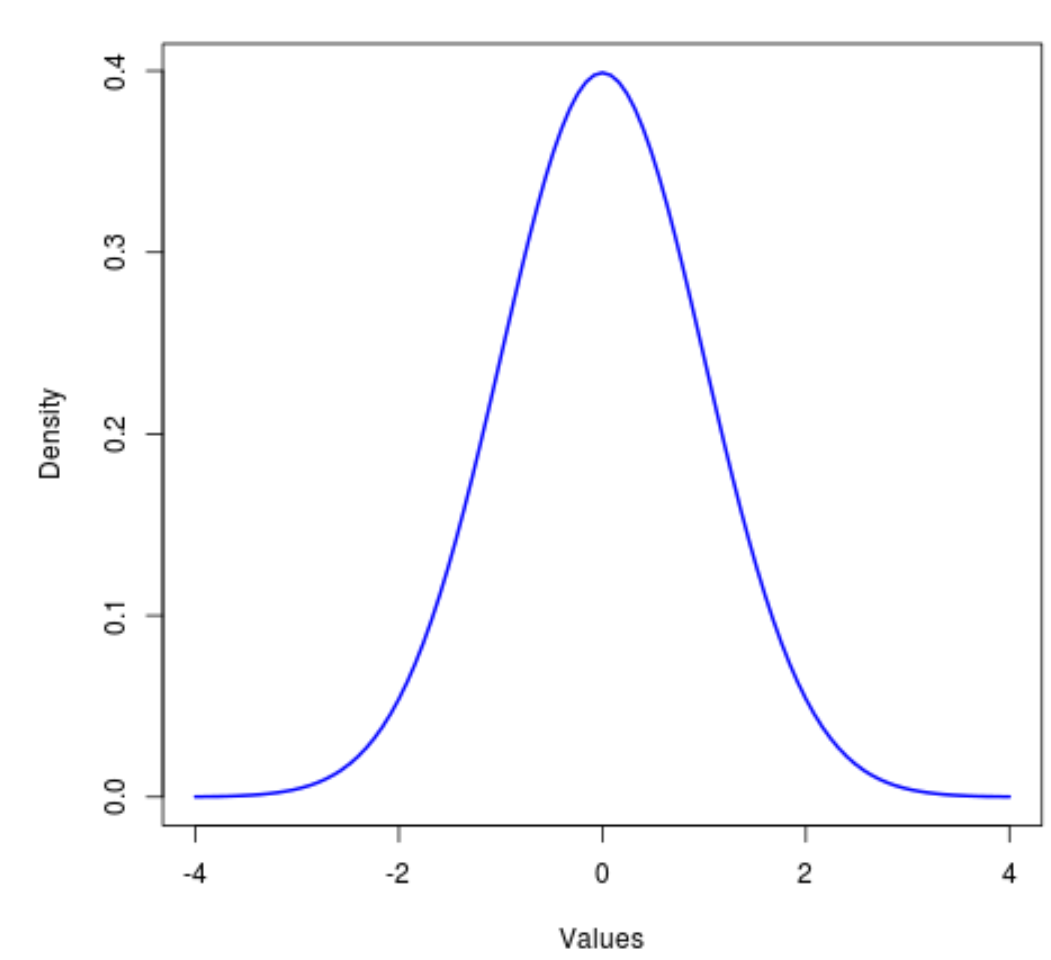
Distribusi yang berkerabat dekat adalah distribusi t , yang juga simetris dan berbentuk lonceng tetapi mempunyai “ekor” yang lebih berat daripada distribusi normal.

Dengan kata lain, lebih banyak nilai dalam distribusi yang terletak di ujung daripada di tengah dibandingkan dengan distribusi normal:

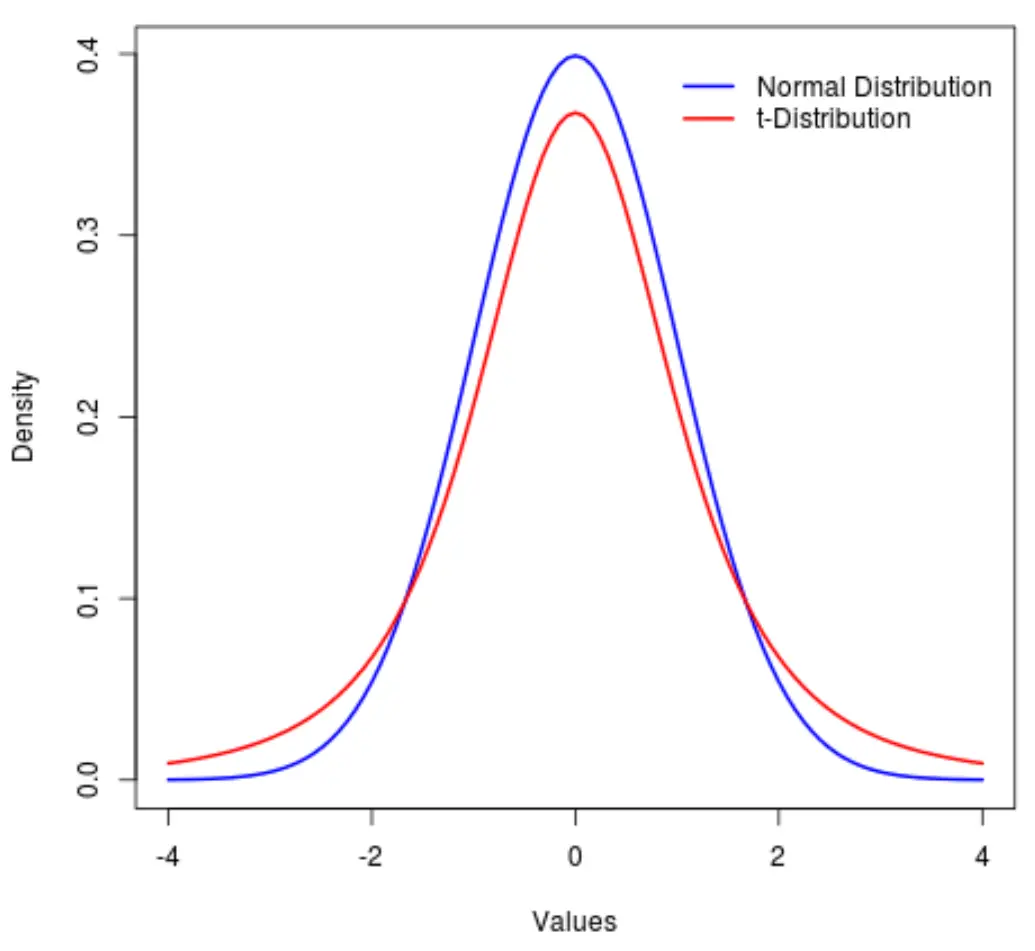
Dalam jargon statistik, kami menggunakan metrik yang disebut kurtosis untuk mengukur seberapa “berat” suatu distribusi. Jadi, kita dapat mengatakan bahwa kurtosis pada distribusi t lebih besar daripada kurtosis pada distribusi normal.

Dalam praktiknya, kita paling sering menggunakan distribusi t saat melakukan pengujian hipotesis atau membangun interval kepercayaan .

Misalnya, rumus menghitung selang kepercayaan untuk rata-rata populasi adalah:

Interval kepercayaan = x +/- t _{1-α/2, n-1} *(s/√ n )

Emas:

• x : mean sampel
• t : nilai t kritis, berdasarkan tingkat signifikansi α dan jumlah sampel n
• s: deviasi standar sampel
• n: ukuran sampel

Dalam rumus ini, kita menggunakan nilai kritis tabel t dan bukan nilai kritis tabel z jika salah satu kondisi berikut ini benar:

• Kami tidak mengetahui deviasi standar populasi.
• Ukuran sampel kurang dari atau sama dengan 30.

Diagram alur berikut memberikan cara yang berguna untuk mengetahui apakah Anda harus menggunakan nilai kritis dari tabel t atau tabel z:

Perbedaan utama antara menggunakan distribusi t dan menggunakan distribusi normal ketika membangun interval kepercayaan adalah bahwa nilai kritis dari distribusi t akan lebih besar, sehingga interval kepercayaan menjadi lebih lebar .

Misalnya, kita ingin membuat interval kepercayaan 95% untuk bobot rata-rata suatu populasi penyu, untuk mengumpulkan sampel acak penyu dengan informasi berikut:

• Ukuran sampel n = 25
• Rata-rata berat sampel x = 300
• Simpangan baku sampel s = 18,5

Nilai kritis z untuk tingkat kepercayaan 95% adalah 1,96 sedangkan nilai t kritis untuk selang kepercayaan 95% dengan df = 25-1 = 24 derajat kebebasan adalah 2,0639 .

Jadi, selang kepercayaan 95% untuk rata-rata populasi yang menggunakan nilai kritis z adalah:

CI 95% = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]

Sedangkan interval kepercayaan 95% untuk mean populasi dengan menggunakan nilai t-kritis adalah:

CI 95% = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]

Perhatikan bahwa interval kepercayaan dengan nilai kritis t lebih lebar.

Idenya di sini adalah ketika kita memiliki ukuran sampel yang kecil, kita kurang yakin akan rata-rata populasi yang sebenarnya, sehingga berguna untuk menggunakan distribusi t untuk menghasilkan interval kepercayaan yang lebih luas yang memiliki peluang lebih besar untuk memuat rata-rata populasi yang sebenarnya.

Visualisasi derajat kebebasan distribusi t

Perlu diperhatikan bahwa dengan bertambahnya derajat kebebasan, distribusi t mendekati distribusi normal.

Untuk menggambarkannya, perhatikan grafik berikut yang menunjukkan bentuk distribusi t dengan derajat kebebasan sebagai berikut:

• df = 3
• df = 10
• df = 30

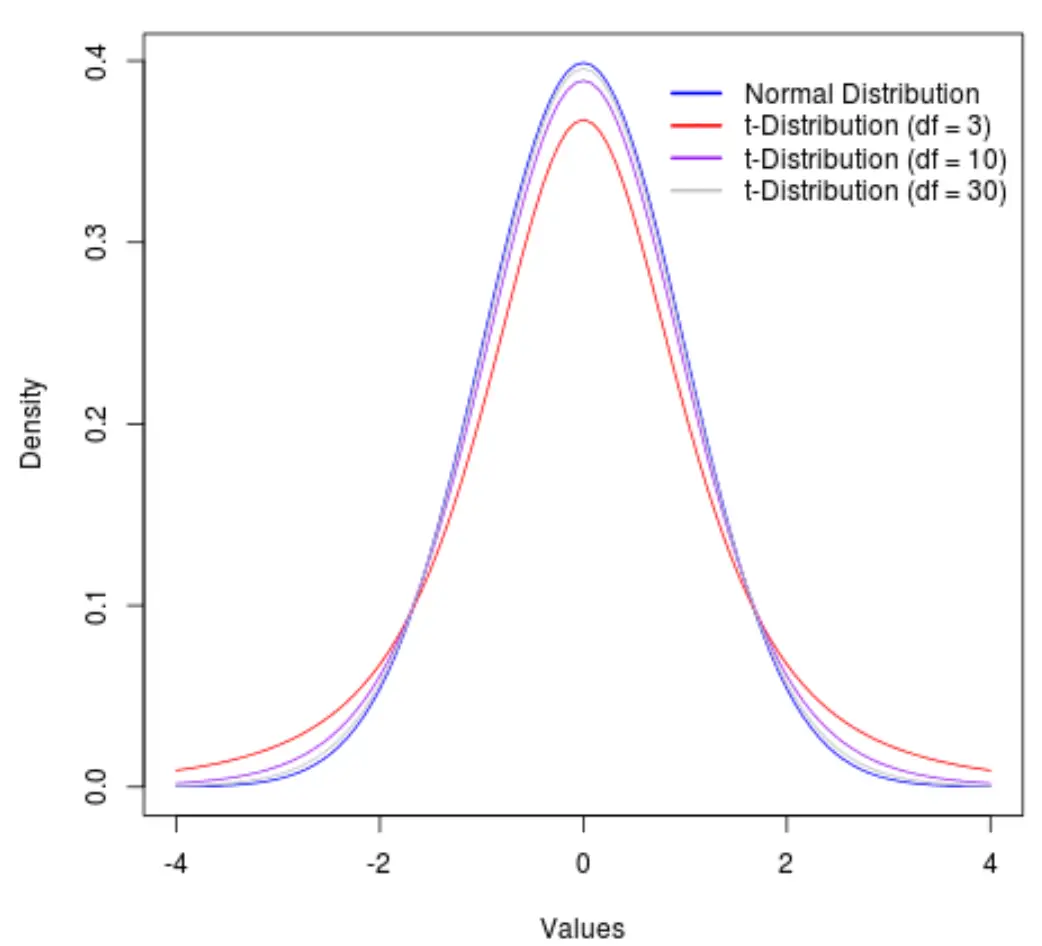
Di luar 30 derajat kebebasan, distribusi t dan distribusi normal menjadi sangat mirip sehingga perbedaan antara penggunaan nilai kritis t dan nilai kritis z dalam rumus menjadi dapat diabaikan.