Apa yang dimaksud dengan distribusi sampling?

Bayangkan ada populasi 10.000 lumba-lumba dan berat rata-rata seekor lumba-lumba dalam populasi tersebut adalah 300 pon.

Jika kita mengambil sampel acak sederhana yang terdiri dari 50 lumba-lumba dari populasi ini, kita mungkin menemukan bahwa berat rata-rata lumba-lumba dalam sampel ini adalah 305 pon.

Kemudian, jika kita mengambil sampel acak sederhana lainnya yang terdiri dari 50 lumba-lumba, kita mungkin menemukan bahwa berat rata-rata lumba-lumba dalam sampel ini adalah 295 pon.

Setiap kali kita mengambil sampel acak sederhana yang terdiri dari 50 lumba-lumba, kemungkinan berat rata-rata lumba-lumba dalam sampel tersebut mendekati rata-rata populasi yaitu 300 pon, namun tidak tepat 300 pon.

Bayangkan kita mengambil 200 sampel acak sederhana yang terdiri dari 50 lumba-lumba dari populasi ini dan membuat histogram berat rata-rata setiap sampel:

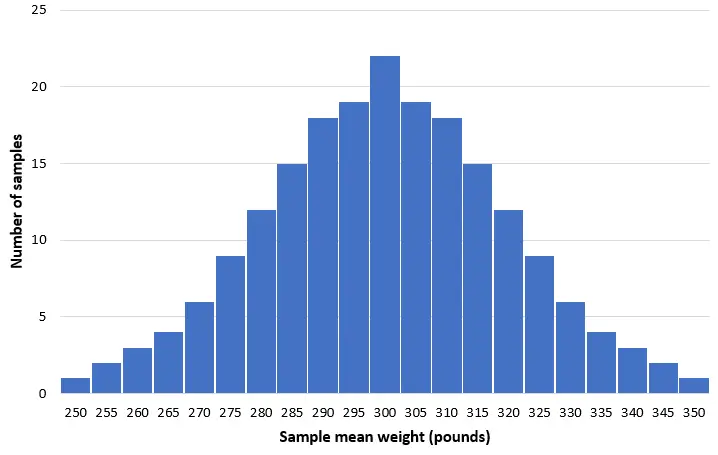
Di sebagian besar sampel, berat rata-rata mendekati 300 pon. Dalam kasus yang jarang terjadi, kami dapat mengambil sampel lumba-lumba kecil yang berat rata-ratanya hanya 250 pon. Atau kita bisa mengambil sampel lumba-lumba hidung botol yang beratnya rata-rata 350 pon. Secara umum, distribusi rata-rata sampel akan mendekati normal, dengan pusat distribusi terletak pada pusat populasi yang sebenarnya.

Distribusi rata-rata sampel ini dikenal sebagai distribusi rata-rata pengambilan sampel dan memiliki sifat-sifat berikut:

_μx = μ

dimana μ _x adalah mean sampel dan μ adalah mean populasi.

_σx = σ/√n

dimana σ _x adalah simpangan baku sampel, σ adalah simpangan baku populasi, dan n adalah ukuran sampel.

Misalnya pada populasi lumba-lumba ini, kita mengetahui bahwa rata-rata berat badannya adalah μ = 300. Jadi mean distribusi samplingnya adalah μ _x = 300 .

Misalkan kita juga mengetahui bahwa simpangan baku populasi adalah 18 pon. Oleh karena itu simpangan baku sampel adalah σ _x = 18/ √50 = 2,546 .

Distribusi proporsi sampel

Bayangkan populasi 10.000 lumba-lumba yang sama. Asumsikan 10% lumba-lumba berwarna hitam dan sisanya berwarna abu-abu. Misalkan kita mengambil sampel acak sederhana yang terdiri dari 50 lumba-lumba dan menemukan bahwa 14% lumba-lumba dalam sampel tersebut berwarna hitam. Selanjutnya, kita mengambil sampel acak sederhana lainnya yang terdiri dari 50 lumba-lumba dan menemukan bahwa 8% lumba-lumba dalam sampel ini berwarna hitam.

Bayangkan kita mengambil 200 sampel acak sederhana yang terdiri dari 50 lumba-lumba dari populasi ini dan membuat histogram proporsi lumba-lumba hitam di setiap sampel:

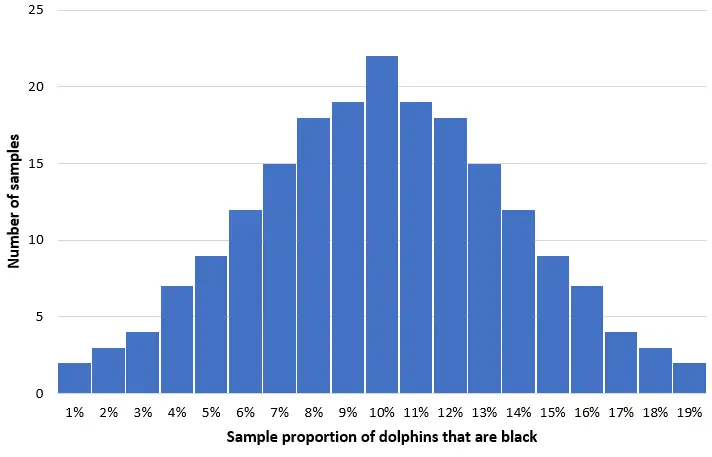
Pada sebagian besar sampel, proporsi lumba-lumba hitam akan mendekati populasi sebenarnya yaitu 10%. Distribusi proporsi sampel lumba-lumba hitam akan mendekati normal, dengan pusat distribusi terletak pada pusat populasi sebenarnya.

Distribusi proporsi sampel ini dikenal sebagai distribusi proporsi sampling dan memiliki sifat-sifat berikut:

_μp = P

dimana p adalah proporsi sampel dan P adalah proporsi populasi.

σ _p = √ (P)(1-P) / n

dimana P adalah proporsi populasi dan n adalah ukuran sampel.

Misalnya pada populasi lumba-lumba ini kita mengetahui bahwa proporsi sebenarnya dari lumba-lumba hitam adalah 10% = 0,1. Jadi, rata-rata distribusi sampling proporsi adalah μ _p = 0,1 .

Misalkan kita juga mengetahui bahwa simpangan baku populasi adalah 18 pon. Jadi, simpangan baku sampelnya adalah σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Membangun keadaan normal

Untuk menggunakan rumus di atas, distribusi sampling harus normal.

Menurut teorema limit pusat , distribusi sampling dari rata-rata sampel mendekati normal jika ukuran sampelnya cukup besar, meskipun distribusi populasinya tidak normal . Dalam kebanyakan kasus, kami menganggap ukuran sampel 30 atau lebih sudah cukup besar.

Distribusi pengambilan sampel dari suatu proporsi sampel mendekati normal jika jumlah keberhasilan dan kegagalan yang diharapkan setidaknya 10.

Contoh

Kita dapat menggunakan distribusi sampling untuk menghitung probabilitas.

Contoh 1: Mesin tertentu membuat cookie. Distribusi berat cookies ini condong ke kanan dengan rata-rata 10 ons dan standar deviasi 2 ons. Jika kita mengambil sampel acak sederhana sebanyak 100 kue kering yang diproduksi oleh mesin ini, berapakah probabilitas berat rata-rata kue kering dalam sampel ini kurang dari 9,8 ons?

Langkah 1: Tetapkan keadaan normal.

Kita perlu memastikan bahwa distribusi pengambilan sampel dari rata-rata sampel adalah normal. Karena ukuran sampel kita lebih besar atau sama dengan 30, berdasarkan teorema limit pusat, kita dapat berasumsi bahwa distribusi sampling dari mean sampel adalah normal.

Langkah 2: Temukan mean dan deviasi standar dari distribusi sampling.

_μx = μ

_σx = σ/√n

μ _x = 10 ons

σ _x = 2/ √100 = 2/10 = 0,2 ons

Langkah 3: Gunakan Kalkulator Area Z-Score untuk menentukan probabilitas bahwa rata-rata berat cookie dalam sampel ini kurang dari 9,8 ons.

Masukkan angka-angka berikut ke dalam Kalkulator Area Skor Z. Anda dapat mengosongkan “Skor Mentah 2” karena kami hanya menemukan satu nomor dalam contoh ini.

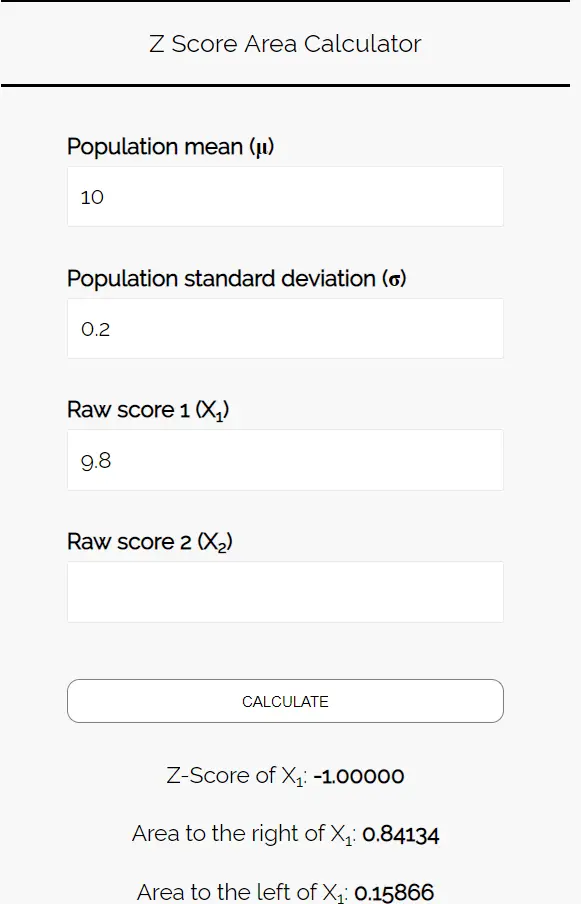
Karena kita ingin mengetahui probabilitas bahwa rata-rata berat kue dalam sampel ini kurang dari 9,8 ons, kita tertarik pada luas di sebelah kiri 9,8. Kalkulator memberi tahu kita bahwa probabilitas ini adalah 0,15866 .

Contoh 2: Menurut penelitian di seluruh sekolah, 87% siswa di sekolah tertentu lebih menyukai pizza daripada es krim. Misalkan kita mengambil sampel acak sederhana sebanyak 200 siswa. Berapa probabilitas bahwa proporsi siswa yang menyukai pizza kurang dari 85%?

Langkah 1: Tetapkan keadaan normal.

Ingatlah bahwa distribusi pengambilan sampel dari suatu proporsi sampel mendekati normal jika jumlah “keberhasilan” dan “kegagalan” yang diharapkan keduanya paling sedikit 10.

Dalam hal ini, perkiraan jumlah siswa yang menyukai pizza adalah 87% * 200 siswa = 174 siswa. Jumlah siswa yang diharapkan tidak menyukai pizza adalah 13% * 200 siswa = 26 siswa. Karena kedua angka tersebut setidaknya berjumlah 10, kita dapat berasumsi bahwa distribusi sampling dari proporsi siswa yang lebih menyukai pizza adalah mendekati normal.

Langkah 2: Temukan mean dan deviasi standar dari distribusi sampling.

_μp = P

σ _p = √ (P)(1-P) / n

_μp = 0,87

σ _p = √ (0,87)(1-0,87) / 200 = 0,024

Langkah 3: Gunakan Kalkulator Area Z-Score untuk menentukan probabilitas bahwa proporsi siswa yang memilih pizza kurang dari 85%.

Masukkan angka-angka berikut ke dalam Kalkulator Area Skor Z. Anda dapat mengosongkan “Skor Mentah 2” karena kami hanya menemukan satu nomor dalam contoh ini.

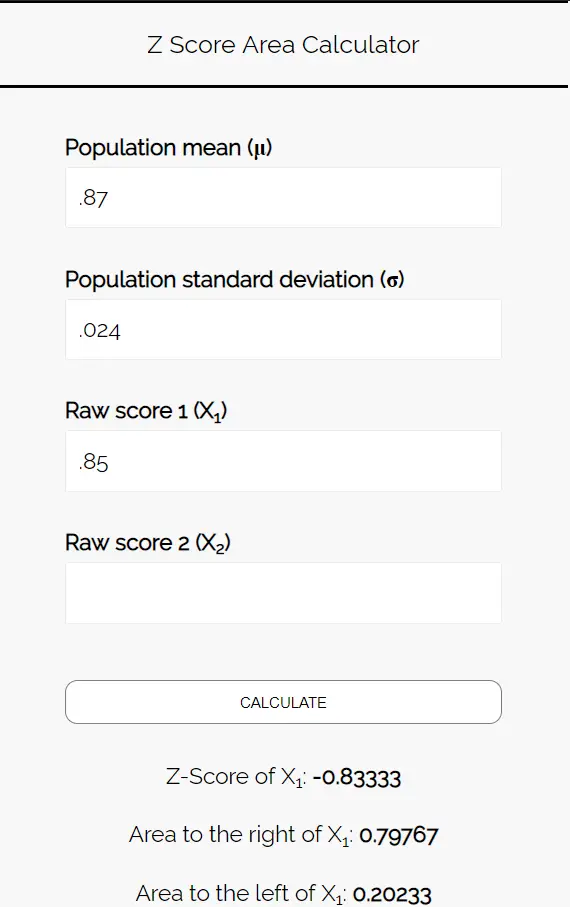
Karena kita ingin mengetahui probabilitas bahwa proporsi siswa yang menyukai pizza kurang dari 85%, kita tertarik pada luas di sebelah kiri 0,85. Kalkulator memberi tahu kita bahwa probabilitas ini adalah 0,20233 .