Pengenalan distribusi rayleigh

Distribusi Rayleigh merupakan distribusi probabilitas kontinu yang digunakan untuk memodelkan variabel acak yang hanya dapat mengambil nilai sama dengan atau lebih besar dari nol.

Ini memiliki fungsi kepadatan probabilitas berikut:

f(x; σ) = (x/σ ² )e ^{-x 2 /(2σ 2 )}

dimana σ adalah parameter skala distribusi.

Sifat-sifat distribusi Rayleigh

Distribusi Rayleigh mempunyai sifat sebagai berikut:

• Rata-rata: σ√ π/2
• Deviasi: ((4-π)/2)σ ²
• Modus: σ

Karena π mempunyai nilai numerik yang diketahui, kita dapat menyederhanakan sifat-sifatnya sebagai berikut:

• Rata-rata: 1,253σ
• Deviasi: 0,429σ ²
• Modus: σ

Visualisasi distribusi Rayleigh

Grafik berikut menunjukkan bentuk distribusi Rayleigh karena mengambil nilai yang berbeda untuk parameter skala:

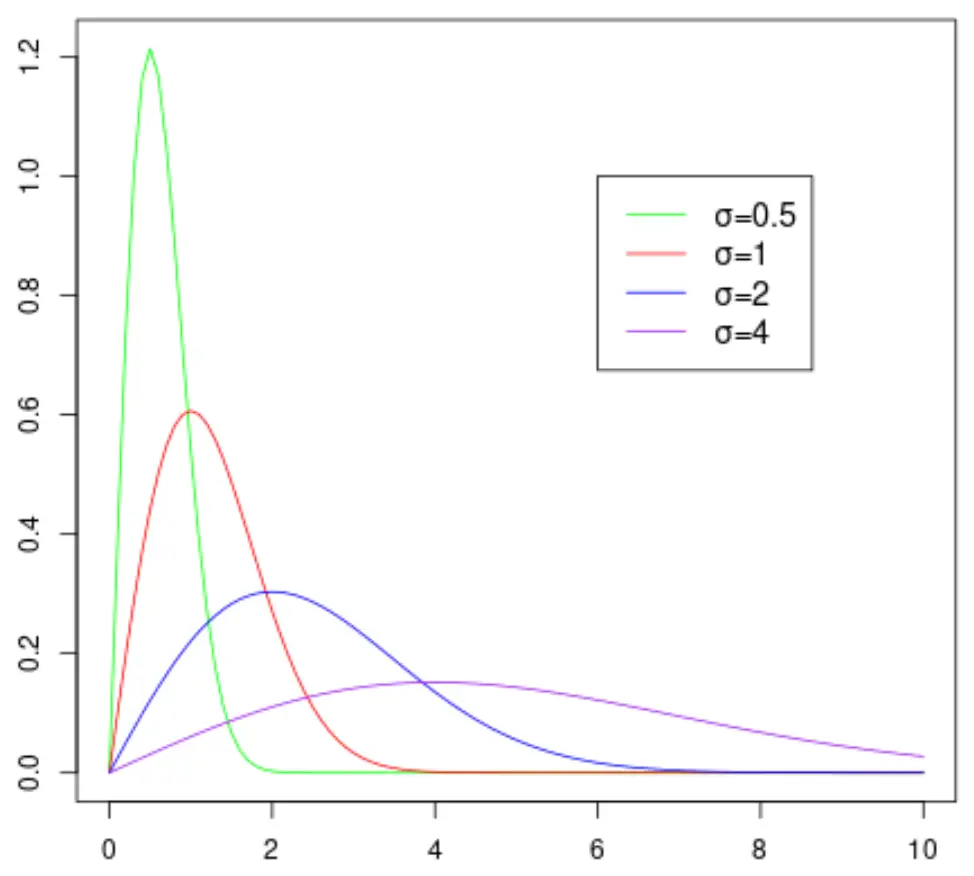
Perhatikan bahwa semakin besar nilai parameter skala σ, semakin luas distribusinya.

Bonus: Bagi yang penasaran, kami menggunakan kode R berikut untuk menghasilkan grafik di atas:

 #load VGAM package
library (VGAM)

#create density plots
curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green')
curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE)
curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE)
curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE)

#add legend
legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"),
       col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)

Hubungan dengan distribusi lain

Distribusi Rayleigh memiliki hubungan berikut dengan distribusi probabilitas lainnya:

1. Jika parameter skala (σ) sama dengan 1, maka distribusi Rayleigh sama dengan distribusi Chi-kuadrat dengan 2 derajat kebebasan.

2. Distribusi Rayleigh merupakan kasus khusus dari distribusi Weibull dengan parameter bentuk k = 2.

3. Distribusi Rayleigh dengan parameter skala σ sama dengan distribusi Rice dengan Rice(0, σ).

Aplikasi

Dalam prakteknya, distribusi Rayleigh digunakan dalam berbagai aplikasi, antara lain:

1. Distribusi Rayleigh digunakan untuk memodelkan perilaku gelombang di lautan, termasuk waktu yang dibutuhkan gelombang untuk mencapai puncaknya dan ketinggian maksimum yang dicapai gelombang.

2. Distribusi Rayleigh digunakan untuk memodelkan perilaku data latar belakang dalam pencitraan resonansi magnetik, yang lebih dikenal dengan MRI.

3. Distribusi Rayleigh digunakan dalam bidang nutrisi untuk memodelkan hubungan antara tingkat nutrisi dan respon nutrisi pada manusia dan hewan.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang distribusi lain dalam statistik:

Pengenalan distribusi normal
Pengenalan distribusi binomial
Pengenalan distribusi Poisson