Cara menghitung distribusi sampling di excel

Distribusi sampling adalah distribusi probabilitas suatu statistik tertentu berdasarkan banyak sampel acak dari satu populasi .

Tutorial ini menjelaskan cara melakukan hal berikut dengan distribusi sampling di Excel:

• Hasilkan distribusi pengambilan sampel.
• Visualisasikan distribusi pengambilan sampel.
• Hitung mean dan deviasi standar distribusi sampling.
• Hitung probabilitas mengenai distribusi sampling.

Hasilkan distribusi pengambilan sampel di Excel

Misalkan kita ingin menghasilkan distribusi sampling yang terdiri dari 1.000 sampel yang masing-masing ukuran sampelnya adalah 20 dan berasal dari distribusi normal dengan mean 5,3 dan standar deviasi 9 .

Kita dapat dengan mudah melakukan ini dengan mengetikkan rumus berikut ke dalam sel A2 spreadsheet kita:

 = NORM . INV ( RAND (), 5.3, 9)

Kita kemudian dapat mengarahkan kursor ke sudut kanan bawah sel hingga tanda + kecil muncul dan menyeret rumus ke kanan sebanyak 20 sel dan ke bawah 1000 sel:

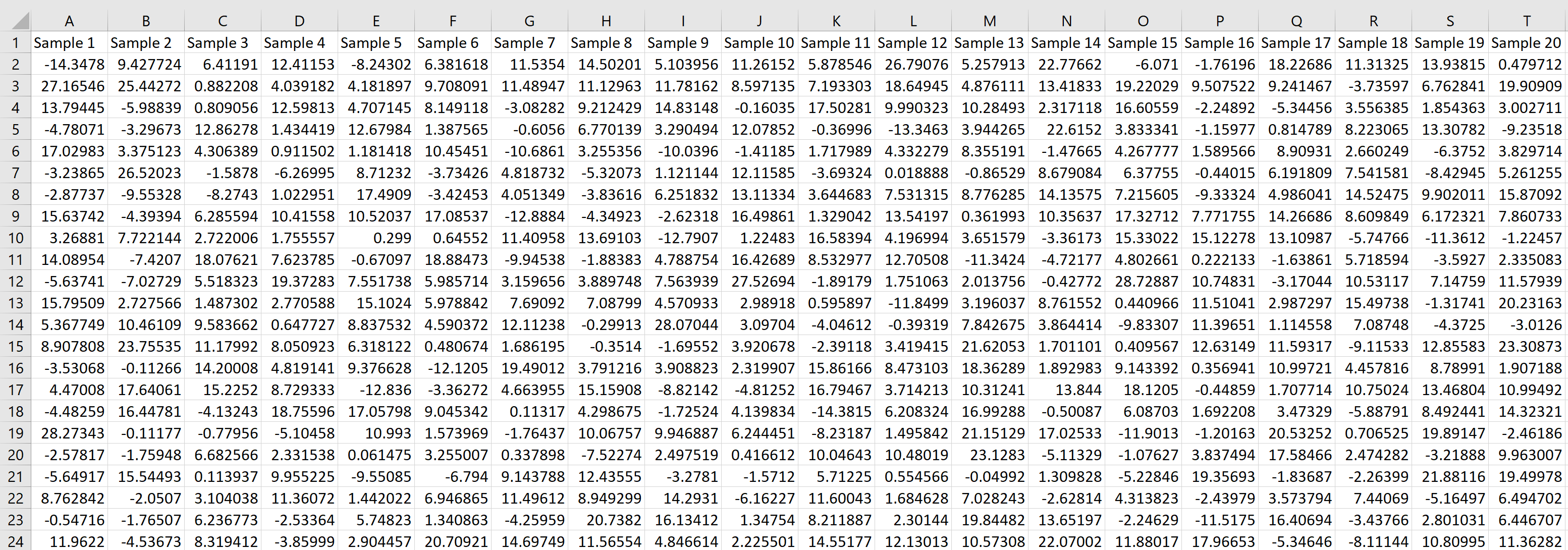
Setiap baris mewakili sampel berukuran 20 yang setiap nilainya berasal dari distribusi normal dengan mean 5,3 dan standar deviasi 9.

Temukan mean dan deviasi standar

Untuk mencari mean dan deviasi standar dari distribusi sampling mean sampel ini, pertama-tama kita dapat mencari mean setiap sampel dengan mengetikkan rumus berikut ke dalam sel U2 pada lembar kerja kita:

 = AVERAGE (A2:T2)

Kita kemudian dapat mengarahkan kursor ke sudut kanan bawah sel hingga tanda + kecil muncul dan klik dua kali untuk menyalin rumus ini ke semua sel lain di kolom U:

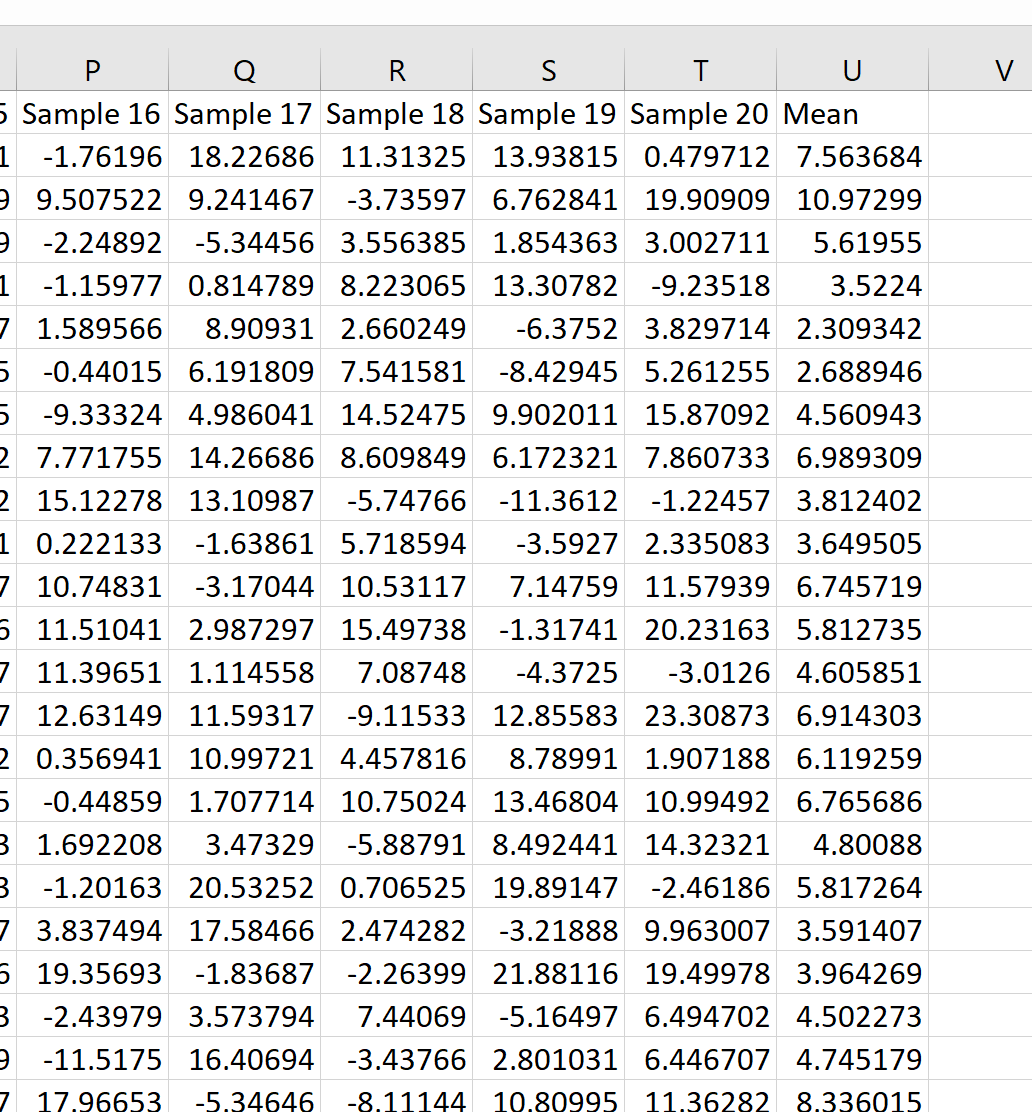
Terlihat sampel pertama mempunyai mean 7,563684, sampel kedua mempunyai mean 10,97299, dan seterusnya.

Kita kemudian dapat menggunakan rumus berikut untuk menghitung mean dan deviasi standar mean sampel:

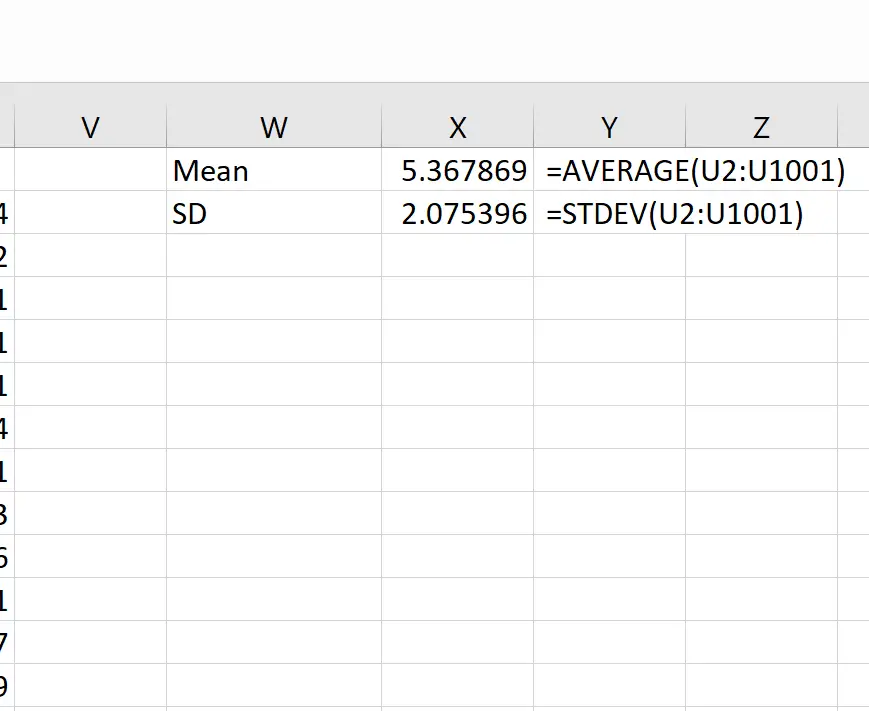
Secara teoritis, rata-rata distribusi sampling harusnya 5,3. Kita dapat melihat bahwa rata-rata sampel sebenarnya dalam contoh ini adalah 5.367869 , yang mendekati 5.3.

Dan secara teori, simpangan baku distribusi sampling harus sama dengan s/√n, yaitu 9 / √20 = 2,012. Kita dapat melihat bahwa simpangan baku sebenarnya dari distribusi sampling adalah 2,075396 , yang mendekati 2,012.

Visualisasikan distribusi pengambilan sampel

Kita juga dapat membuat histogram sederhana untuk memvisualisasikan distribusi sampling dari rata-rata sampel.

Untuk melakukannya, cukup sorot semua mean sampel di kolom U, klik tab Sisipkan , lalu klik opsi Histogram di bawah bagian Bagan .

Ini memberikan histogram berikut:

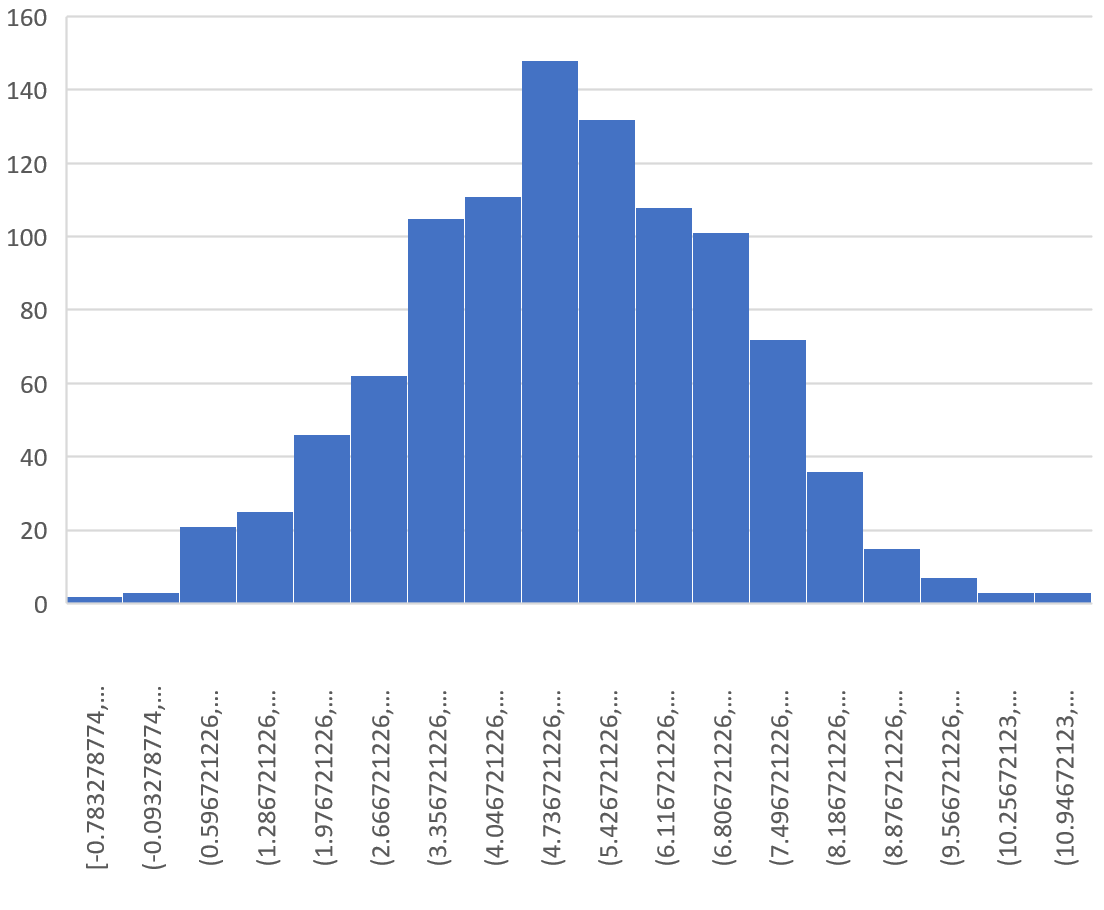
Terlihat distribusi samplingnya berbentuk lonceng dengan puncak mendekati nilai 5.

Namun dari ekor distribusinya kita dapat melihat bahwa beberapa sampel memiliki mean lebih besar dari 10 dan sampel lainnya memiliki mean kurang dari 0.

Hitung probabilitasnya

Kita juga dapat menghitung probabilitas memperoleh nilai rata-rata sampel tertentu, berdasarkan rata-rata populasi, deviasi standar populasi, dan ukuran sampel.

Misalnya, kita dapat menggunakan rumus berikut untuk mencari probabilitas bahwa mean sampel kurang dari atau sama dengan 6, jika mean populasi adalah 5,3, deviasi standar populasi adalah 9, dan ukuran sampel adalah:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

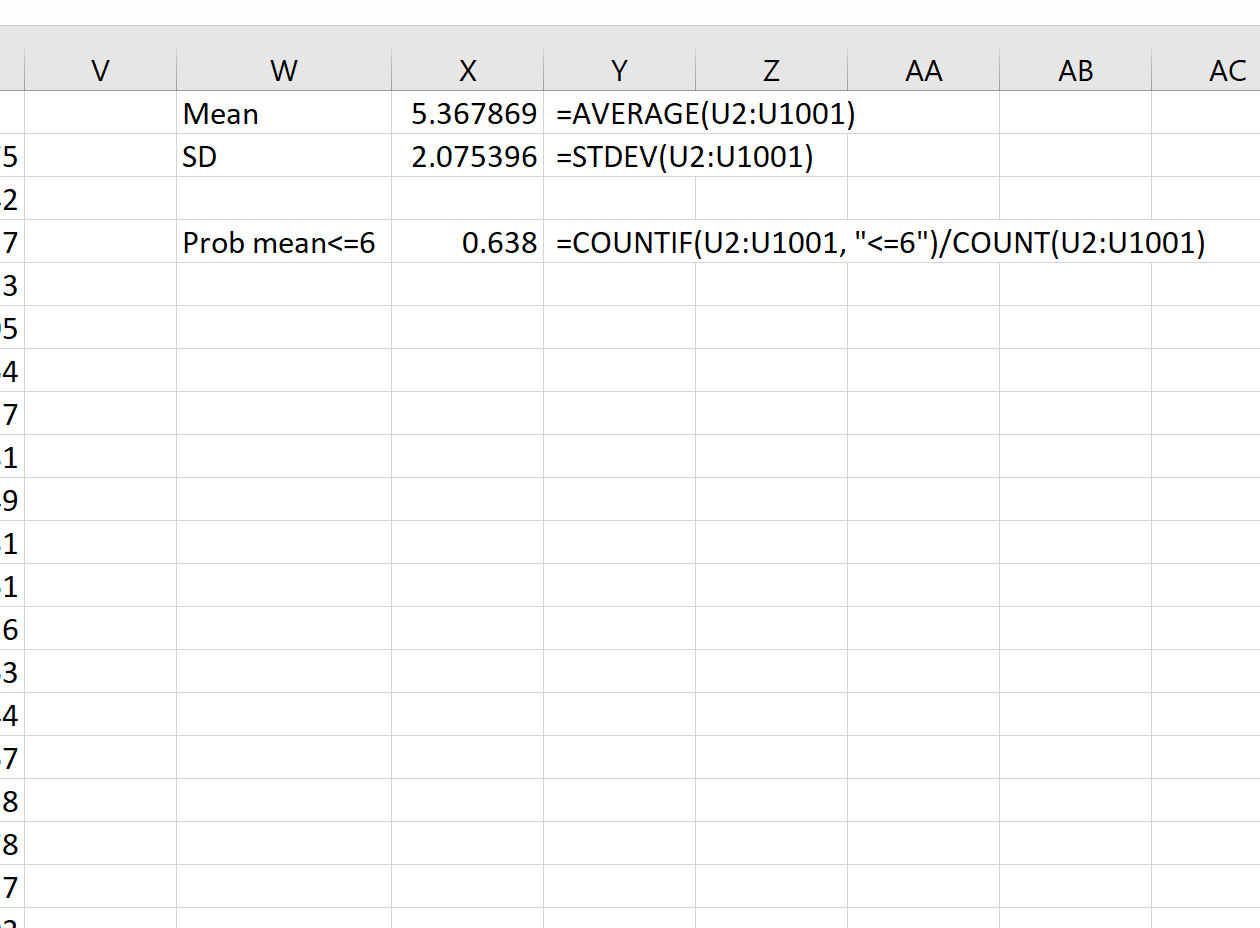
Kita melihat bahwa probabilitas mean sampel kurang dari atau sama dengan 6 adalah 0,638.

Ini sangat dekat dengan probabilitas yang dihitung oleh Kalkulator Distribusi Sampling :

Sumber daya tambahan

Pengantar Distribusi Sampling
Kalkulator Distribusi Sampling
Pengantar Teorema Limit Pusat