Distribusi sampling perbedaan proporsi
Artikel ini menjelaskan apa perbedaan distribusi sampling proporsi dan kegunaannya dalam statistik. Perbedaan rumus distribusi pengambilan sampel proporsi dan latihan penyelesaian langkah demi langkah juga disajikan.
Berapakah distribusi sampling dari perbedaan proporsinya?
Perbedaan distribusi proporsi sampling adalah distribusi yang dihasilkan dari perhitungan selisih proporsi sampling seluruh kemungkinan sampel dari dua populasi yang berbeda.
Artinya, proses memperoleh distribusi sampling dari perbedaan proporsinya adalah, pertama, mengekstraksi semua sampel yang mungkin dari dua populasi yang berbeda, kedua, menentukan proporsi setiap sampel yang diekstraksi, dan terakhir, menentukan perbedaan antara semua sampel yang diambil. proporsi perbedaan proporsi. dua populasi. Sehingga himpunan hasil yang diperoleh setelah melakukan operasi tersebut membentuk distribusi sampling selisih proporsinya.

Dalam statistik, distribusi sampel perbedaan proporsi digunakan untuk menghitung probabilitas bahwa perbedaan antara proporsi sampel dari dua sampel yang dipilih secara acak mendekati perbedaan proporsi populasi.
Rumus Distribusi Sampling Selisih Proporsi
Sampel yang dipilih berdasarkan perbedaan proporsi distribusi pengambilan sampel ditentukan oleh distribusi binomial , karena untuk tujuan praktis, proporsi adalah rasio kasus yang berhasil terhadap jumlah total observasi.
Namun demikian, karena teorema limit pusat, distribusi binomial dapat didekati dengan distribusi probabilitas normal . Oleh karena itu, distribusi sampling selisih proporsinya dapat didekati dengan distribusi normal dengan ciri-ciri sebagai berikut:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
Catatan: Distribusi sampling dari perbedaan proporsi hanya dapat didekati dengan distribusi normal jika
![]()
,
![]()
,
![]()
,
![]()
,
![]()
Dan
![]()
.
Oleh karena itu, karena distribusi sampling selisih proporsi dapat didekati dengan distribusi normal, maka rumus menghitung statistik distribusi sampling selisih proporsi adalah sebagai berikut:

Emas:
-

adalah proporsi sampel i.
-

adalah proporsi penduduk i.
-

adalah probabilitas kegagalan populasi i,

.
-

adalah ukuran sampel i.
-

adalah variabel yang ditentukan oleh distribusi normal standar N(0,1).
Rumus ini mirip dengan rumus pengujian hipotesis perbedaan proporsi.
Contoh konkrit distribusi sampling perbedaan proporsi
Setelah melihat pengertian Distribusi Sampling Selisih Proporsi dan apa rumusnya, di bawah ini Anda dapat melihat contoh penyelesaiannya langkah demi langkah untuk menyelesaikan pemahaman konsepnya.
- Anda ingin menganalisis keakuratan dua pabrik produksi, satu pabrik memproduksi sedemikian rupa sehingga hanya 5% suku cadang yang diproduksi memiliki cacat, sedangkan persentase suku cadang cacat di pabrik lain adalah 8%. Jika kita mengambil sampel sebanyak 200 suku cadang dari pabrik pertama dan sampel lain sebanyak 280 suku cadang dari pabrik kedua, berapa peluang persentase cacat pada pabrik produksi pertama lebih besar daripada persentase cacat pada pabrik kedua? produksi?
Untuk menyelesaikan mengetahui semua data masalahnya, pertama-tama kita akan menghitung proporsi bagian yang berproduksi dengan baik dari setiap pabrik:
![Rendered by QuickLaTeX.com \begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7c02732cc5fb319bfa5bf7b8ed8d03db_l3.png)
Jika tingkat cacat pada pabrik pertama lebih besar dibandingkan dengan tingkat cacat pada pabrik kedua, maka persamaan berikut ini benar:
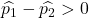
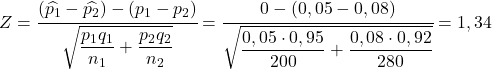
Jadi, peluang tingkat kecacatan pabrik pertama lebih besar daripada tingkat kecacatan pabrik kedua setara dengan peluang variabel Z lebih besar dari 1,34:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”242″ style=”vertical-align: -5px;”></p>
</p>
<p> Terakhir, kita hanya perlu mencari probabilitas yang sesuai di <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-41dd897cdff473ff488cde0e3cc140b0_l3.png) tabel distribusi normal dan kita sudah menyelesaikan masalahnya:
tabel distribusi normal dan kita sudah menyelesaikan masalahnya:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”319″ style=”vertical-align: -5px;”></p>
</p>
<p> Singkatnya, probabilitas proporsi cacat pada pabrik pertama lebih besar dibandingkan proporsi cacat pada pabrik kedua adalah 9,01%. </p>
<div style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d6e503a2089d30be8fd68bbc722bb44_l3.png)