Pengenalan distribusi segitiga

Distribusi segitiga merupakan distribusi probabilitas kontinu dengan fungsi kepadatan probabilitas berbentuk segitiga.

Ini ditentukan oleh tiga nilai:

• Nilai minimumnya adalah
• Nilai maksimumb
• Nilai maksimum c

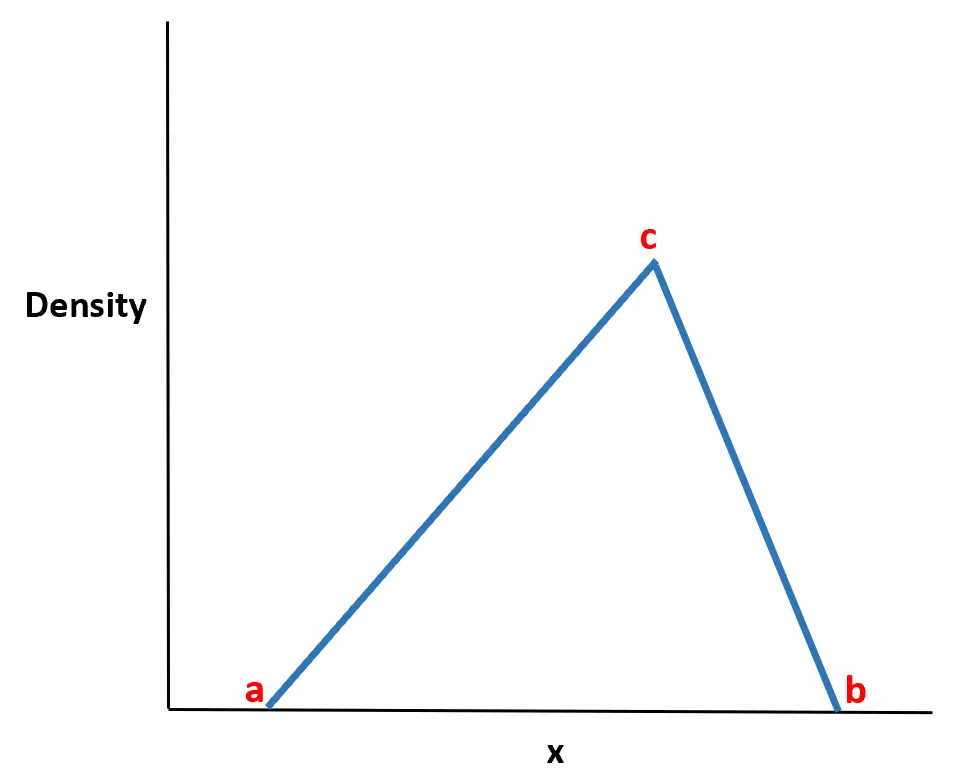
Nama distribusinya berasal dari fakta bahwa fungsi kepadatan probabilitas berbentuk segitiga.

Ternyata distribusi ini sangat berguna di dunia nyata karena kita sering kali dapat memperkirakan nilai minimum (a), nilai maksimum (b), dan nilai yang paling mungkin (c) yang akan diambil oleh suatu variabel acak . sering kali dapat memodelkan perilaku variabel acak menggunakan distribusi segitiga hanya dengan mengetahui ketiga nilai ini.

Misalnya, sebuah restoran mungkin memperkirakan bahwa total penjualannya untuk minggu mendatang adalah minimal $10.000, maksimal $30.000, dan kemungkinan besar $25.000.

Hanya dengan menggunakan ketiga angka ini, mereka dapat menggunakan distribusi segitiga untuk menentukan probabilitas menghasilkan sejumlah penjualan tertentu.

Sifat-sifat distribusi segitiga

Distribusi segitiga mempunyai sifat-sifat sebagai berikut:

PDF:

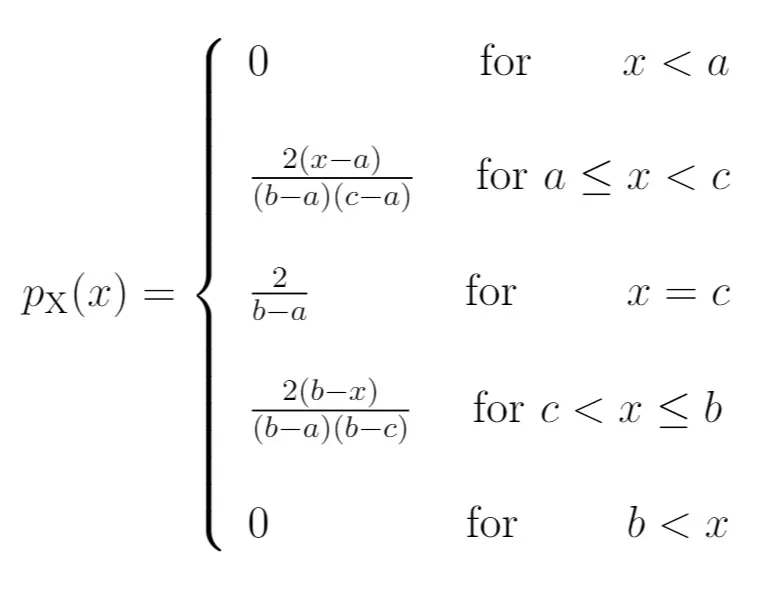
CDF:

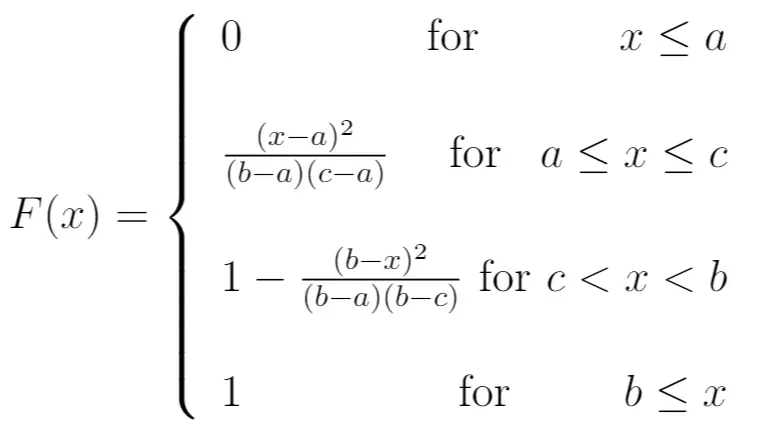
Rata-rata: (a + b + c) / 3

Modus: c

Varians: (a ² + b ² + c ² – ab – ac – bc) / 18

Contoh penggunaan distribusi segitiga

Mari kita kembali ke contoh sebelumnya. Katakanlah sebuah restoran memperkirakan total penjualannya untuk minggu mendatang adalah minimal $10.000, maksimal $30.000, dan kemungkinan besar $25.000.

Berapa probabilitas restoran tersebut mempunyai total penjualan kurang dari $20.000?

Untuk menjawab pertanyaan ini, kita dapat menanyakan x = total penjualan. Kita tahu bahwa x terletak di antara nilai minimum a sebesar $10.000 dan nilai maksimum c sebesar $25.000.

Jadi, berdasarkan PDF, kita dapat menggunakan persamaan berikut untuk mencari probabilitas bahwa restoran tersebut memiliki total penjualan kurang dari $20.000:

• P(X < $20.000) = (xa) ² / ((ba)(ca))
• P(X < $20.000) = (20.000-10.000) ² / ((30.000-10.000)(25.000-10.000))
• P(X < $20.000) = 0,333

Peluang restoran tersebut mempunyai total penjualan kurang dari $20.000 adalah 0,333 .

Berapa rata-rata penjualan yang diharapkan untuk restoran tersebut?

Kita dapat menghitung rata-rata penjualan yang diharapkan menggunakan rumus rata-rata yang diberikan sebelumnya:

• Rata-rata = (a + b + c) / 3
• Rata-rata = ($10.000 + $30.000 + $25.000) / 3
• Rata-rata = $21.667

Rata-rata penjualan yang diharapkan adalah 21.667 .

Sumber daya tambahan

Tutorial berikut memberikan pengenalan tentang distribusi lain yang umum digunakan:

Distribusi normal
Distribusi binomial
Distribusi Ikan
Distribusi geometris