Pengantar distribusi seragam
Distribusi seragam adalah distribusi probabilitas yang setiap nilai antara interval a sampai b mempunyai peluang terjadinya yang sama.
Jika suatu variabel acak X mengikuti distribusi seragam, maka peluang X mengambil nilai antara x 1 dan x 2 dapat dicari dengan rumus berikut:
P(x 1 < X < x 2 ) = (x 2 – x 1 ) / (b – a)
Emas:
- x 1 : nilai bunga yang lebih rendah
- x 2 : nilai bunga tertinggi
- a: nilai minimum yang mungkin
- b : nilai maksimum yang mungkin
Misalnya, berat lumba-lumba tersebar merata antara 100 dan 150 pon.
Jika kita memilih seekor lumba-lumba secara acak, kita dapat menggunakan rumus di atas untuk menentukan probabilitas bahwa lumba-lumba yang terpilih memiliki berat antara 120 dan 130 pon:
- P(120 < X < 130) = (130 – 120) / (150 – 100)
- P(120 < X < 130) = 10/50
- P(120 < X < 130) = 0,2
Peluang terambilnya lumba-lumba yang terpilih memiliki berat antara 120 dan 130 pon adalah 0,2 .
Visualisasikan distribusi seragam
Jika kita membuat plot kepadatan untuk memvisualisasikan pemerataan, maka akan terlihat plot berikut:
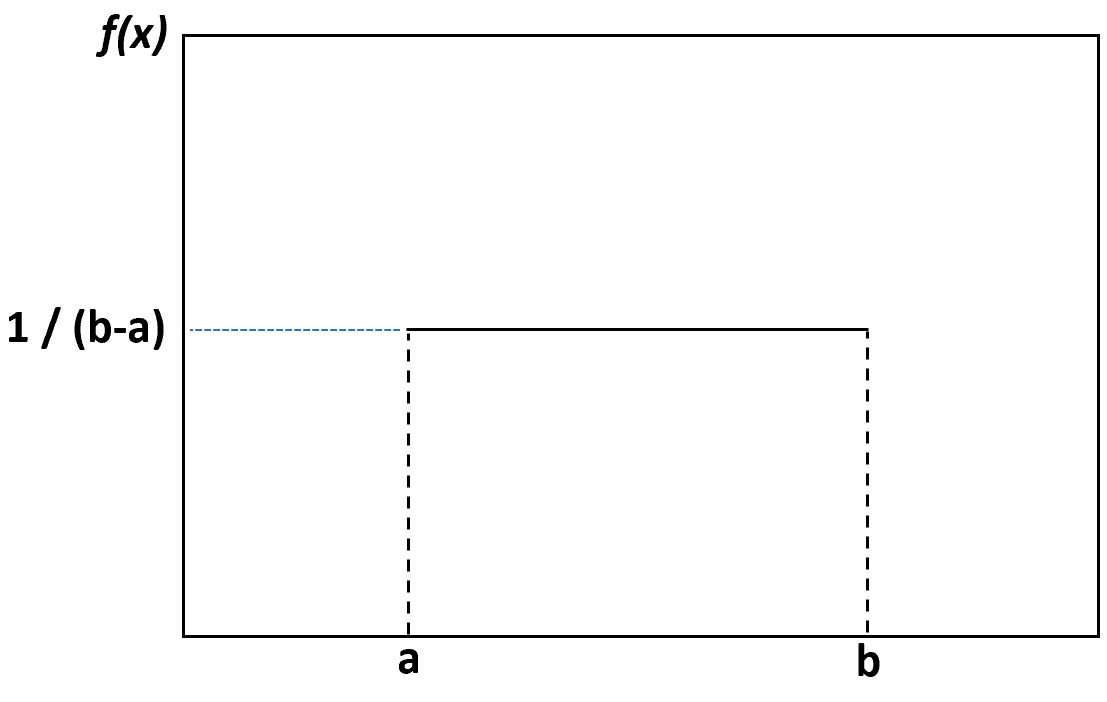
Setiap nilai antara batas bawah a dan batas atas b mempunyai peluang terjadinya yang sama dan nilai apa pun di luar batas tersebut mempunyai peluang nol.
Misalnya, dalam contoh sebelumnya, kami mengatakan bahwa berat lumba-lumba didistribusikan secara merata antara 100 dan 150 pon. Berikut cara memvisualisasikan distribusi ini:
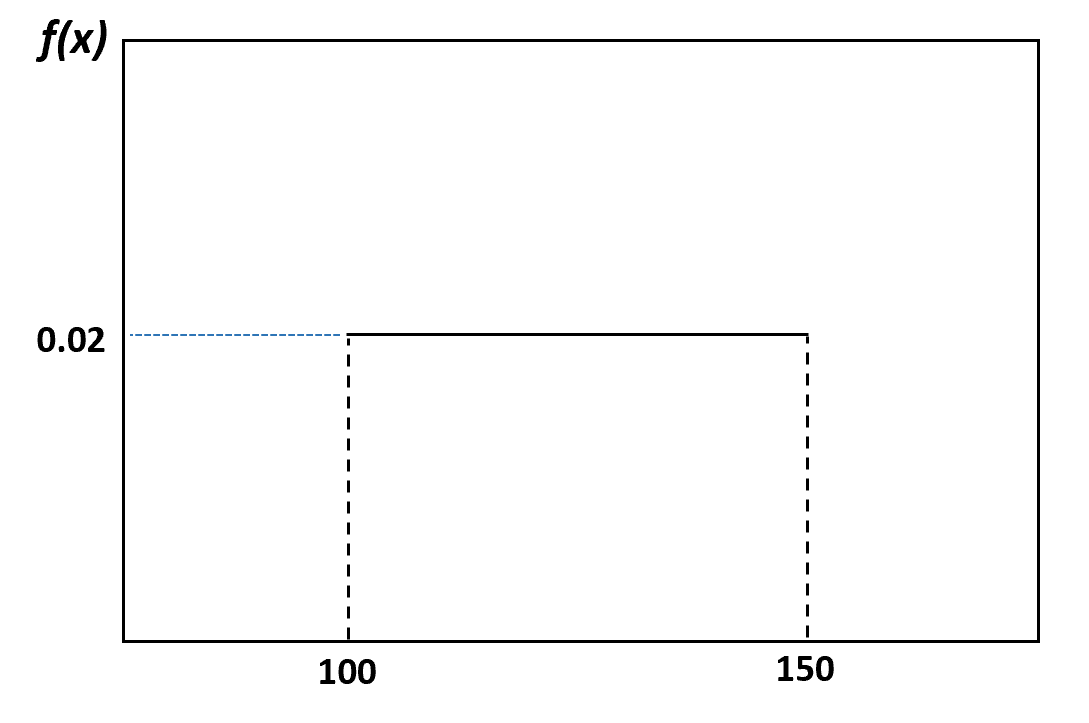
Dan probabilitas seekor lumba-lumba yang dipilih secara acak memiliki berat antara 120 dan 130 pon dapat divisualisasikan sebagai berikut:
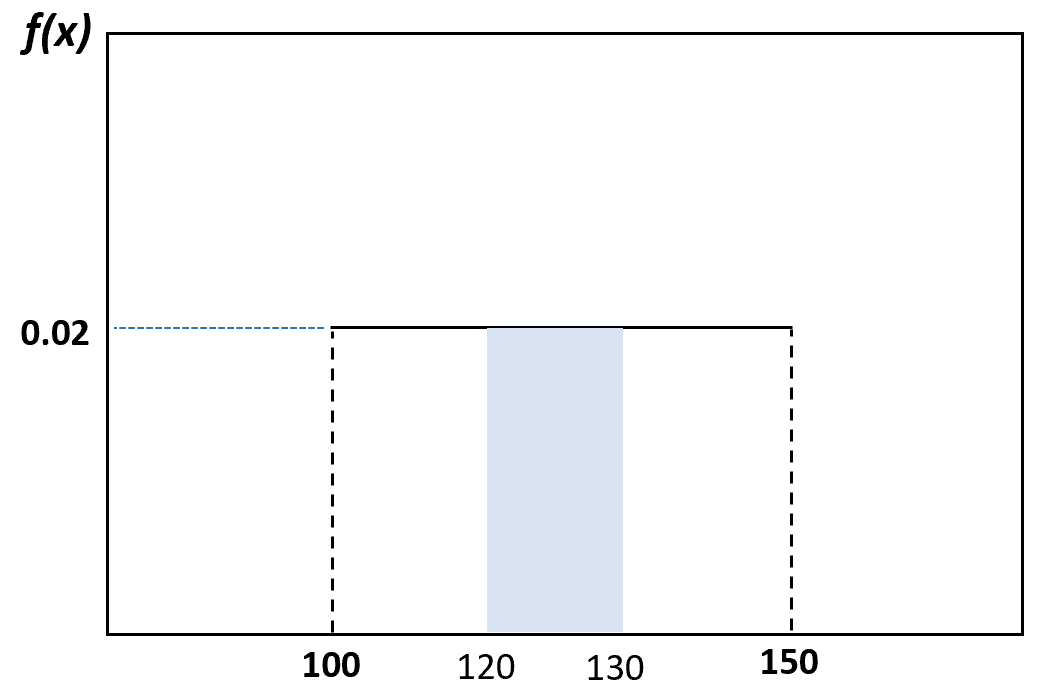
Sifat distribusi seragam
Distribusi seragam mempunyai ciri-ciri sebagai berikut:
- Rata-rata: (a + b) / 2
- Median: (a + b) / 2
- Simpangan baku: √ (b – a) 2/12
- Selisih : (b – a) 2/12
Misalnya, berat lumba-lumba tersebar merata antara 100 dan 150 pon.
Kita dapat menghitung properti berikut untuk distribusi ini:
- Berat rata-rata: (a + b) / 2 = (150 + 100) / 2 = 125
- Berat rata-rata: (a + b) / 2 = (150 + 100) / 2 = 125
- Standar deviasi berat: √ (150 – 100) 2/12 = 14,43
- Variasi berat: (150 – 100) 2/12 = 208,33
Masalah dengan Praktik Distribusi Seragam
Gunakan soal latihan berikut untuk menguji pengetahuan Anda tentang distribusi seragam.
Pertanyaan 1: Sebuah bus datang ke halte setiap 20 menit. Jika Anda tiba di halte bus, berapa peluang bus tersebut tiba dalam waktu 8 menit atau kurang?
Solusi 1: Waktu tunggu minimum adalah 0 menit dan waktu tunggu maksimum adalah 20 menit. Nilai bunga bawah adalah 0 menit dan nilai bunga atas adalah 8 menit.
Jadi, kami akan menghitung probabilitasnya sebagai berikut:
P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .
Pertanyaan 2: Durasi permainan NBA didistribusikan secara merata antara 120 dan 170 menit. Berapa peluang suatu pertandingan NBA yang dipilih secara acak berlangsung lebih dari 155 menit?
Solusi 2: Durasi minimum adalah 120 menit dan durasi maksimum adalah 170 menit. Nilai bunga bawah 155 menit dan nilai bunga atas 170 menit.
Jadi, kami akan menghitung probabilitasnya sebagai berikut:
P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .
Pertanyaan 3: Berat suatu spesies katak tertentu tersebar merata antara 15 dan 25 gram. Jika seekor katak diambil secara acak, berapa peluang terambilnya katak dengan berat antara 17 dan 19 gram?
Solusi 3: Berat minimal 15 gram dan berat maksimal 25 gram. Nilai bunga bawah sebesar 17 gram dan nilai bunga atas sebesar 19 gram.
Jadi, kami akan menghitung probabilitasnya sebagai berikut:
P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .
Catatan: Kita dapat menggunakan Kalkulator Distribusi Seragam untuk memeriksa jawaban kita terhadap setiap soal ini.