Distribusi t siswa
Artikel ini menjelaskan apa itu distribusi Student t dan kegunaannya. Selain itu juga ditampilkan grafik distribusi t Student dan apa saja ciri-ciri dari jenis distribusi probabilitas tersebut.
Apa distribusi Siswa?
Distribusi t Student adalah distribusi probabilitas yang banyak digunakan dalam statistik. Secara khusus, distribusi t Student digunakan dalam uji t Student untuk menentukan perbedaan antara rata-rata dua sampel dan untuk menetapkan interval kepercayaan.
Distribusi t Student dikembangkan oleh ahli statistik William Sealy Gosset pada tahun 1908 dengan nama samaran “Student”.
Distribusi t Student ditentukan oleh jumlah derajat kebebasannya, yang diperoleh dengan mengurangkan satu satuan dari jumlah total observasi. Oleh karena itu, rumus untuk menentukan derajat kebebasan distribusi t Student adalah ν=n-1 .
![Rendered by QuickLaTeX.com \begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png)
Grafik distribusi t siswa
Setelah kita mengetahui definisi distribusi t Student, mari kita lihat apa grafiknya. Nah, di bawah ini Anda dapat melihat secara grafis beberapa contoh distribusi t Student dengan derajat kebebasan yang berbeda-beda.
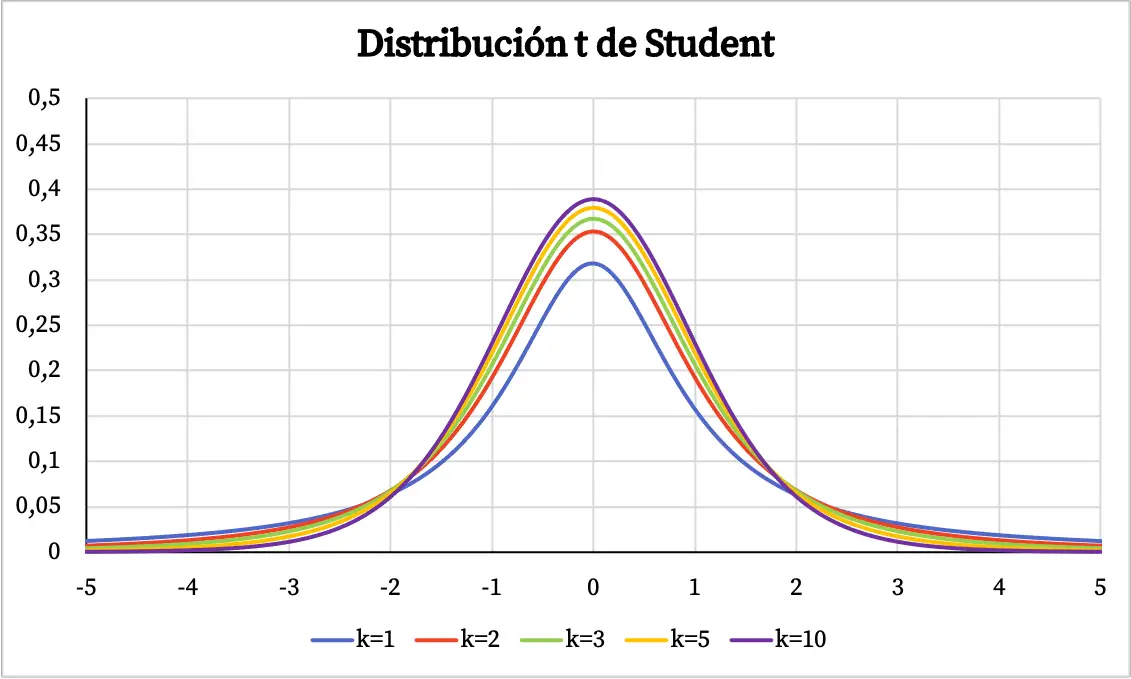
Dari grafik distribusi t Student dapat disimpulkan sifat-sifat sebagai berikut:
- Distribusi Student t simetris berpusat pada 0 dan berbentuk lonceng.
- Distribusi t Student lebih tersebar dibandingkan distribusi normal, yaitu kurva distribusi t Student lebih lebar.
- Semakin besar derajat kebebasan distribusi t Student, semakin rendah penyebarannya.
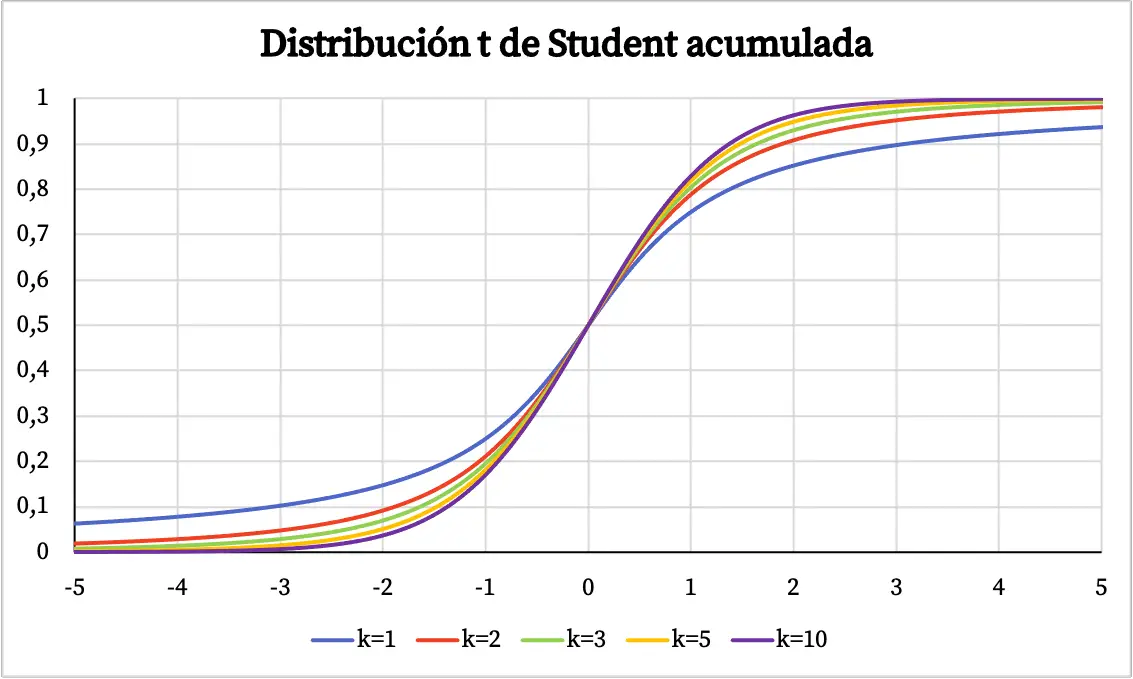
Pada grafik di atas, fungsi kepadatan distribusi t Student telah diplot terhadap derajat kebebasannya. Namun, Anda dapat melihat di bawah bagaimana fungsi probabilitas kumulatif dari distribusi t Student bervariasi:
Karakteristik distribusi t Student
Karakteristik terpenting dari distribusi t Student ditunjukkan di bawah ini.
- Domain distribusi Student t terdiri dari bilangan real.
![]()
- Untuk distribusi t Student dengan lebih dari satu derajat kebebasan, mean distribusinya sama dengan 0.
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=”Rendered by QuickLaTeX.com” height=”55″ width=”190″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Varians dari distribusi t Student dapat dihitung dengan menggunakan ekspresi berikut:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png)
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”245″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Median dan modus distribusi t Student, berapa pun jumlah derajat kebebasannya, selalu 0.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png)
- Fungsi kepadatan distribusi Student t ditentukan dengan rumus berikut:
![]()
- Fungsi distribusi probabilitas kumulatif dari distribusi t Student ditentukan dengan rumus berikut:
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png)
- Untuk distribusi t Student dengan derajat kebebasan lebih besar dari 3, koefisien asimetrinya adalah nol karena merupakan distribusi simetris.
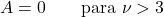
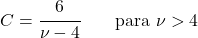 Penerapan distribusi t Siswa
Penerapan distribusi t Siswa
Distribusi t Student adalah distribusi probabilitas yang banyak digunakan dalam statistik. Faktanya, terdapat uji-t Student, yang digunakan untuk menguji hipotesis dan interval kepercayaan.
Jadi, distribusi t Student memungkinkan kita menganalisis perbedaan rata-rata dua sampel, lebih tepatnya, digunakan untuk menentukan apakah dua sampel mempunyai rata-rata yang berbeda secara signifikan. Demikian pula uji t Student digunakan untuk mengetahui apakah garis yang diperoleh dari analisis regresi linier mempunyai kemiringan atau tidak.
Singkatnya, penerapan distribusi t Student mengandalkan analisis kumpulan data yang secara teoritis mengikuti distribusi normal tetapi jumlah observasi terlalu kecil untuk menggunakan jenis distribusi ini.