Distribusi normal standar

Artikel ini menjelaskan apa itu distribusi normal standar dan kegunaannya. Anda juga akan menemukan properti distribusi normal standar, tabel dengan nilai karakteristiknya, dan, sebagai tambahan, latihan yang diselesaikan.

Berapakah distribusi normal standarnya?

Distribusi normal standar , juga disebut distribusi normal satuan , adalah kasus distribusi normal yang paling sederhana. Lebih tepatnya distribusi normal baku adalah distribusi normal dengan nilai mean dan deviasi standar masing-masing sama dengan 0 dan 1.

Oleh karena itu, distribusi normal baku didefinisikan sebagai N(0,1), dengan parameter pertama adalah mean distribusi dan parameter kedua adalah simpangan baku (atau SD).

Oleh karena itu, grafik distribusi normal standarnya adalah sebagai berikut:

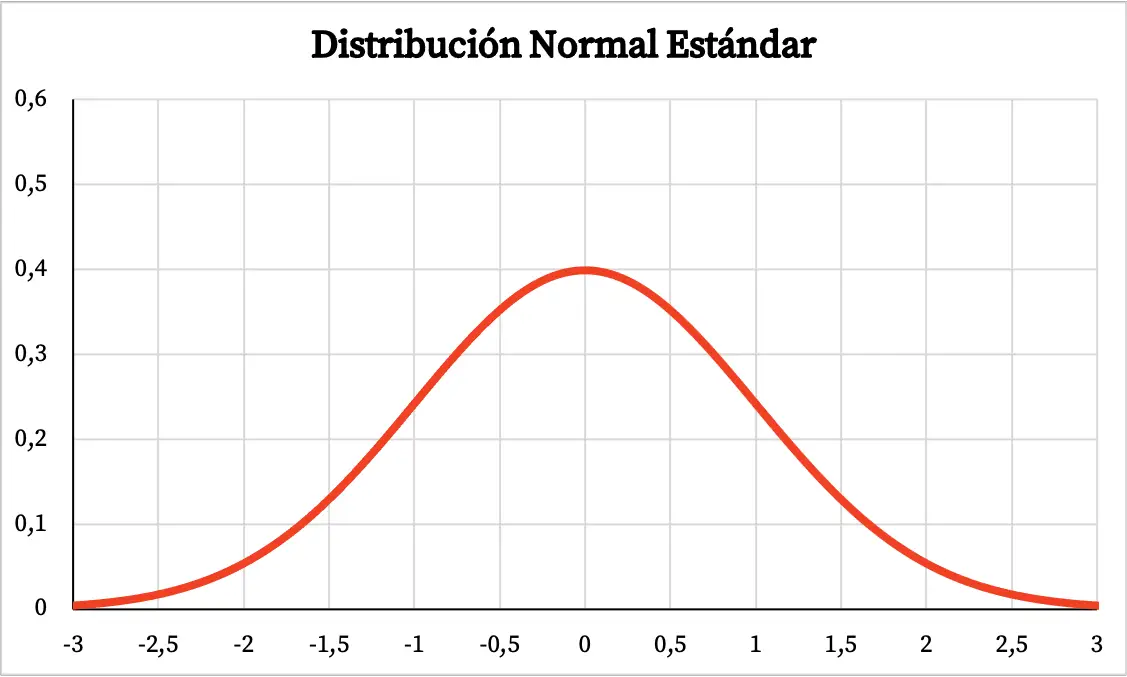
Rumus distribusi normal standar

Untuk mengubah distribusi normal menjadi distribusi normal standar, Anda harus mengurangi rata-rata distribusi normal dari semua nilainya dan kemudian membaginya dengan simpangan baku dari distribusi normal tersebut.

Oleh karena itu, rumus distribusi normal standar adalah sebagai berikut:

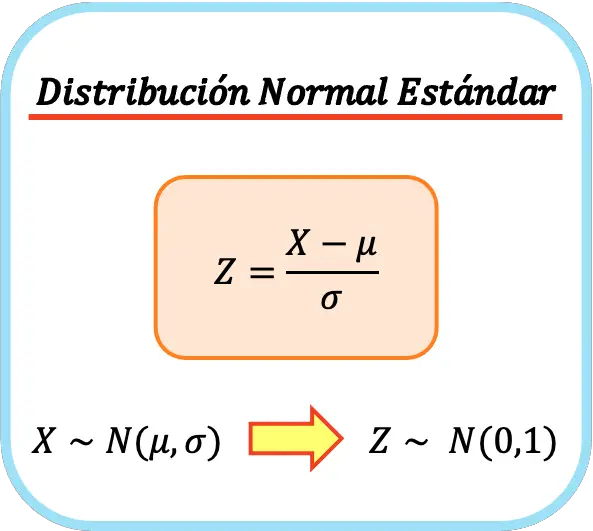
Dengan cara ini mean aritmatika dan simpangan baku variabel baru masing-masing akan menjadi 0 dan 1, sehingga diperoleh distribusi normal baku. Proses ini disebut juga normalisasi univariat atau normalisasi univariat .

Tabel distribusi normal standar

Tabel distribusi normal baku adalah tabel yang berisi probabilitas suatu nilai yang diamati lebih kecil dari nilai tertentu dari distribusi normal baku.

Selain itu, karena fungsi distribusi normal bergantung pada mean dan deviasi standarnya, tabel distribusi normal standar juga digunakan untuk menentukan probabilitas distribusi normal. Untuk melakukan ini, distribusi normal diketik ke dalam distribusi normal standar dan kemudian kita melihat di tabel berapa probabilitas yang sesuai dengannya.

Jadi, nilai pada tabel distribusi normal standar adalah sebagai berikut:

Contoh Distribusi Normal Standar

Setelah kita mengetahui pengertian distribusi normal baku dan apa rumusnya, berikut adalah contoh konkritnya untuk memahami konsep tersebut dengan baik.

• Suatu variabel acak kontinu mengikuti distribusi normal dengan mean 45 dan standar deviasi 15, berapakah peluang memperoleh nilai kurang dari atau sama dengan 58?

Untuk mencari peluang berdistribusi normal kita perlu menggunakan tabel fiturnya, namun untuk itu kita perlu melakukan proses pengetikan terlebih dahulu untuk mendapatkan standar berdistribusi normal. Oleh karena itu kami menggunakan rumus distribusi normal standar:

Jadi kita kurangi mean dari nilai probabilitas lalu bagi dengan standar deviasi

Setelah kita membakukan variabelnya, kita pergi ke tabel probabilitas distribusi normal standar (lihat di atas) untuk melihat probabilitas apa yang sesuai dengan nilai 0,87:

Oleh karena itu, probabilitas memperoleh nilai yang sama dengan atau kurang dari 58 adalah 80,78%.

Ciri-ciri distribusi normal standar

Distribusi normal standar mempunyai ciri-ciri sebagai berikut:

• Distribusi normal baku adalah distribusi simetris yang berpusat pada 0.
• Seperti distribusi normal, grafik distribusi normal standar berbentuk lonceng, dengan sebagian besar area grafik berada di sekitar mean.
• Oleh karena itu, mean, modus, dan median suatu distribusi normal mempunyai nilai yang sama, yaitu 0.
• Distribusi normal standar memiliki maksimum pada z=0.
• Demikian pula, distribusi normal standar memiliki dua titik belok, di z=-1 dan z=+1.
• Berdasarkan aturan praktisnya, kita mengetahui bahwa 68% nilai berada dalam distribusi normal standar antara +1 dan -1, 95% nilai antara +2 dan -2, dan 99,7% nilai antara + 3 dan – 3.